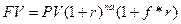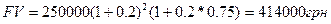Тема 2 Наращивание по сложной схеме. Сложные проценты
Рассмотрим ситуацию:
В банк ложится вклад под r % годовых.
В первый год: 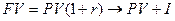
Во 2-й год: 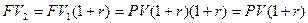
В 3-й год: 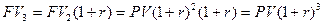
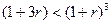
Основная формула начисления по сложной форме
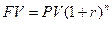
где n- количество лет
Пример 1: Рассчитать наращенную сумму по сложной и простой схемам, если начальная сумма 100000 грн. количество лет – 3 года под 20% годовых.
Решение
Дано:
PV=100000 грн.
n=3 года
r=20%
FV-?
По простой схеме:
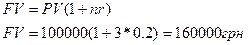
По сложной схеме:
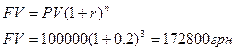
Вывод: при n>1 нарощенная сумма (FV) по сложной схеме начисления больше чем по простой.
Пример 2: Рассчитать наращенную сумму по простой и сложной схемам, если начальная сумма вклада 100000грн ложится на 6 месяцев под 20 % годовых.
Решение
Дано:
PV=100000 грн.
r=20%
n=0,5 года
FV-?
По простой схеме:
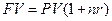
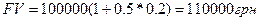
По сложной схеме:
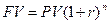
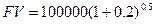
Вывод: При n<1 нарощенная сумма (FV) по сложной схеме начисления меньше чем FV по простой схеме.
Считаем, что вклад сделан на условиях сложных процентов, если следующий годовой доход І рассчитывается не на начальную сумму PV, а на общую суму, которая включает также насчитанные раньше проценты.
Процедуры присоединения начисленных процентов к базе расчёта начисленных процентов называется капитализация (начисление процентов на проценты)
При использовании сложной схемы начисления база для расчёта дохода І всё время увеличивается.
Особенности использования сложных схем:
1. На практике очень часто изменяются проценты ставки, тогда определение наращенной суммы при изменяющейся ставки процента имеет вид:
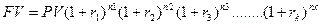
где 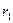 ,
, 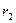 ,
, 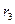 ….
…. 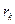 - процентные ставки действующие в определённых периодах.
- процентные ставки действующие в определённых периодах.
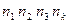 - длительность определённых периодов.
- длительность определённых периодов.
Пример 3 Предприятие разместило в банк 250000 грн на таких условиях: 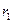 =14% - действует на протяжении 2-х лет,
=14% - действует на протяжении 2-х лет, 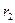 =16% - на 2 года,
=16% - на 2 года, 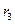 =18% - на 3 года. Определить нарощенную сумму через 7 лет
=18% - на 3 года. Определить нарощенную сумму через 7 лет
Решение
Дано:
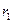 =14%
=14%
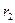 =16%
=16%
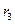 =18 %
=18 %
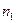 =1 год
=1 год
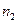 =2 года
=2 года
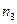 = 3 года
= 3 года
FV-?

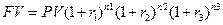
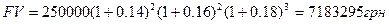
В финансовых расчётах базовый период (промежуток времени) 1 год, но на практике капитализация процентов проводиться несколько раз в год. Тогда говорят про m-кратные начисления.
В таком случае FV определяется по формуле:
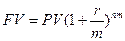
Где m-количество интервалов в 1 году
Пример 4 Проанализировать изменения размеров наращенной суммы на конец двухгодового периода. Если процент насчитывается:
1) ежегодно
2) по полугодиям
3) по кварталам
4) по месяцам
Решение
1) 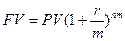 =
= 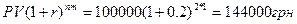
2) 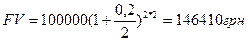
3) 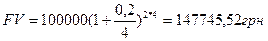
4) 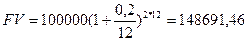
Вывод: Чем чаще насчитывается процент (меньше интервал начисления) при одних и тех же начальных условиях, тем больше наращенная сума
В этом случае говорят, что начальная ставка при m=1 называется номинальной.
Наращивание по сложной схеме если общее число периодов или интервалов не является целым числом. В таком случае используется 2 схемы наращивания:
1) Обычная сложная схема
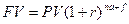
Где, na – целое число лет
f – дробная часть
2) Смешанная схема начисления
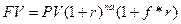
Где na – целое число лет
f – дробная часть
Пример 5 Фирма получила кредит в размере 250000 грн с термином погашения через 2 года 9 месяцев. Определить сумму погашения и прибыль банка, если процентная ставка 20 %.
Решение
Дано
PV=250000 грн
n=2 года
f= 9/12=0,75
FV-?
1-й способ:
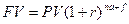
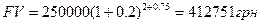
2-й способ: