Определение текущей стоимости. Дисконтирование

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной будущей сумме FV, которую следует уплатить или получить через некоторое время, необходимо рассчитать современную, текущую сумму PV полученной ссуды или вклада в банк. Такая ситуация может возникнуть: при разработке контракта, при определении текущей стоимости векселя (см. главу "Операции с векселями") и в обычных жизненных условиях.

По формуле простых процентов (1.4)

PV = - , (1.9)

где t - срок финансовой сделки в днях, T - число дней в году, r - годовая процентная ставка. Знак минус указывает на то, что в финансовых операциях настоящая и будущая суммы всегда имеют противоположные знаки.

Расчет PV по FV необходим и тогда, когда проценты с суммы удерживаются вперед, непосредственно при выдаче кредита, ссуды. В этих случаях говорят, что сумма FV дисконтируется, или учитывается, сам процесс начисления процентов и их удержания называют учетом, а удержанные проценты - дисконтом, или скидкой D.

D=FV-PV, (1.10)
где FV и PV берутся в (1.10) по абсолютной величине.

Отношение v=PV/FV называют дисконтным или дисконтирующим множителем. По формуле простых процентов

v=1/(1+ 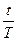×r). (1.11)

По формуле сложных процентов (1.6) текущая сумма вклада или текущая стоимость векселя записывается в виде

, (1.12)

где m - число раз начисления процентов в году, k - срок дисконтирования.

Дисконтирующий множитель

v = . (1.13)

Пример 1.5 Клиент должен получить в конце года 10000 руб. На какой вклад ему выгоднее положить деньги: простой или срочный с ежемесячным начислением процентов. Годовая процентная ставка в обоих случаях 16%

Решение. Дисконтирующий множитель по простым процентам

v=1/(1+r t/T)=1/(1+0,16)=0,862069, PV= - FV·v =10000·0,862= - 8620,69 руб. Дисконтирующий множитель по сложным процентам v=1/(1+r/m)^(m k)=1/(1+0,16/12)^12=0,853045 PV=-FV v=10000·0,853045= - 8530,45 руб.

FV=10000

t=T

m=12

r=0,16

k=1

PV=?

Совершенно очевидно, что срочный вклад выгоднее клиенту, так как в начале года по нему нужно вложить на 90 руб. меньше, чем по простому вкладу.

Определение срока ссуды (вклада)

По формуле простых процентов (1.4) срок финансовой сделки определяется в днях t

t= , (1.14)

где T принятое число дней в году (см. раздел 1.2).

По формуле сложных процентов (1.6) срок финансовой сделки определяется в годах k

. (1.15)

В выражениях (1.14) и (1.15) r - номинальная ставка; текущая PV и будущая FV суммы берутся по абсолютной величине.

Определение размера процентной ставки

Нередко возникает вопрос, под какую ставку нужно дать кредит в сумме PV, чтобы через определенный срок получить обратно сумму FV?

По формуле простых процентов

. (1.16)

По формуле сложных процентов

. (1.17)