Замечательные пределы

Первым замечательным пределом называется

.

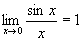Вторым замечательным пределом называется

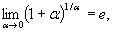его можно записать в другом виде: ,

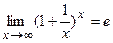где e » 2.718281…- число Эйлера.

На практике также используются формулы для пределов последовательности:

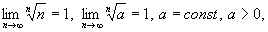
Используются на практике и формулы вида:

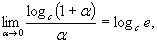
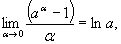
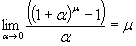, в частности,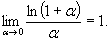

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах.

В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.

Пусть в банк положено 100 ден. ед. из расчета 100% годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100×(1+1/3)³»237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100 × (1 +1/10)¹⁰ » 259 (ден. ед.),

100 × (1+1/100)¹⁰⁰ » 270 (ден. ед.),

100 × (1+1/1000)¹⁰⁰⁰ » 271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что

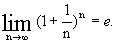
Пример. Найти предел последовательности, заданной общим членом .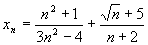

Решение. Применим теорему о пределе суммы и найдем предел каждого слагаемого. При n ®¥ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему о пределе частного. Поэтому сначала преобразуем x_n, разделив числитель и знаменатель первого слагаемого на n², а второго на n. Затем, применяя теорему о пределе частного и о пределе суммы, найдем:

.

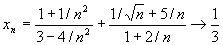Пример. 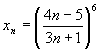. Найти .

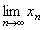Решение. .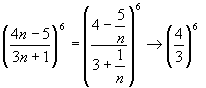

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример. Найти ( ).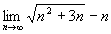

Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида ¥ - ¥. Преобразуем формулу общего члена:

.

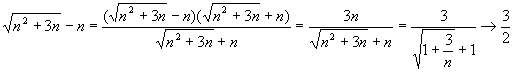Пример. Найти .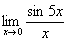

Решение. Имеем: 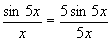. Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу первого замечательного предела, получим .

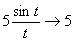Пример. Вычислить .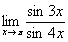

Решение. Обозначим y=p-x. Тогда при x®p, y®0.Имеем:

sin 3x = sin 3(p-y) = sin (3p-3y) = sin 3y и sin 4x = sin 4(p-y) = sin (4p-4y)= - sin 4y.

.

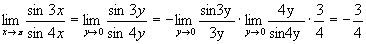Пример. Найти .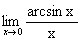

Решение. Обозначим arcsin x=t. Тогда x=sint и при x®0 t®0. .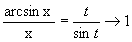

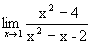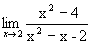Пример. Найти 1) ; 2) ; 3) .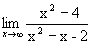

Решение.

1. Применяя теорему 1 о пределе разности и произведения, находим предел знаменателя: .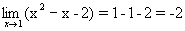

Предел знаменателя не равен нулю, поэтому, по теореме 1 о пределе частного, получаем: .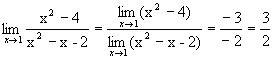

2. Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ¹ 2 равенство:

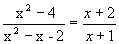
Так как 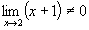, то по теореме о пределе частного найдем

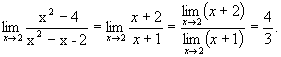
3. Числитель и знаменатель при x®¥ являются бесконечно большими функциями. Поэтому теорема о пределе частного непосредственно не применима. Разделим числитель и знаменатель на x² и к полученной функции применим теорему о пределе частного:

.

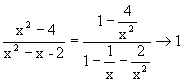Пример. Найти .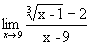

Решение. Здесь числитель и знаменатель стремятся к нулю: 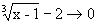, x-9®0, т.е. имеем неопределенность вида .

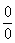Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения 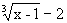, получим

.

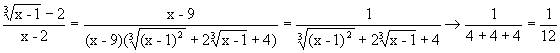Пример. Найти .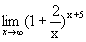

Решение. 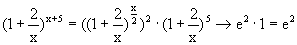.