Наращение и дисконтирование

Наращенная сумма при дискретных процентах определяется по формуле

S=P(1+j/m)^mn,

где j - номинальная ставка процентов, а m - число периодов начисления процентов в году.

Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m®¥ имеем

S=limP(1+j/m)^mn=P lim [(1+j/m)^m]ⁿ. (45)

^{m®¥ m®¥}

Известно, что

lim (1+j/m)^m=lim [(1+j/m)^m/j]^j=e^j,

^{m®¥ m®¥}

где e - основание натуральных логарифмов.

Используя этот предел в выражении (45), окончательно получаем, что наращенная сумма в случае непрерывного начисления процентов по ставкеj равна

S=Pe^jn. (46)

Для того, чтобы отличать ставку непрерывных процентов от ставок дискретных процентов, ее называют силой роста и обозначают символом d. Тогда

S=Pe^dn. (47)

Сила ростаd представляет собой номинальную ставку процентов при m®¥.

Дисконтирование на основе непрерывных процентных ставок осуществляется по формуле

P=Se^dn. (48)

Связь дискретных и непрерывных процентных ставок

Дискретные и непрерывные процентные ставки находятся в функциональной зависимости, благодаря которой можно осуществлять переход от расчета непрерывных процентов к дискретным и наоборот. Формулу эквивалентного перехода от одних ставок к другим можно получить путем приравнивания соответствующих множителей наращения

(1+i)ⁿ=e^dn. (49)

Из записанного равенства следует, что

d=ln(1+i), (50)

i=e^d-1. (51)

Пример 13.

Годовая ставка сложных процентов равна 15%, чему равна эквивалентная сила роста,

Решение.

Воспользуемся формулой (50)

d=ln(1+i)=ln(1+0,15)=0,13976,

т.е. эквивалентная сила роста равна 13,976%.

Расчет срока ссуды и процентных ставок

В ряде практических задач начальная (P) и конечная (S) суммы заданы контрактом, и требуется определить либо срок платежа, либо процентную ставку, которая в данном случае может служить мерой сравнения с рыночными показателями и характеристикой доходности операции для кредитора. Указанные величины нетрудно найти из исходных формул наращения или дисконтирования. По сути дела, в обоих случаях решается в известном смысле обратная задача.

Срок ссуды

При разработке параметров соглашения и оценивании сроков достижения желательного результата требуется определить продолжительность операции (срока ссуды) через остальные параметры сделки. Рассмотрим этот вопрос подробнее.

А) При наращивании по сложной годовой ставке i. Из исходной формулы наращения

S=P(1+i)ⁿ

следует, что

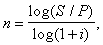(52)

где логарифм можно взять по любому основанию, поскольку он имеется как в числителе, так и в знаменателе.

Б) При наращивании по номинальной ставке процентов m раз в году из формулы

S=P(1+j/m)^mn

получаем

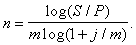(53)

В) При дисконтировании по сложной годовой учетной ставке d. Из формулы

P=S(1-d)ⁿ

имеем 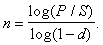(54)

Г) При дисконтировании по номинальной учетной ставке mраз в году. Из

P=S(1-f/m)^mn

приходим к формуле

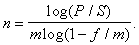(55)

При наращивании по постоянной силе роста. Исходя из

S=Pe^dn

получаем

ln(S/P)=dn. (56)

Расчет процентных ставок

Из тех же исходных формул, что и выше, получим выражения для процентных ставок.

А) При наращивании по сложной годовой ставке i. Из исходной формулы наращения

S=P(1+i)ⁿ

следует, что

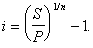(57)

Б) При наращивании по номинальной ставке процентов m раз в году из формулы

S=P(1+j/m)^mn

получаем 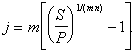(58)

В) При дисконтировании по сложной годовой учетной ставке d. Из формулы

P=S(1-d)ⁿ

имеем 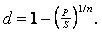(59)

Г) При дисконтировании по номинальной учетной ставке mраз в году. Из

P=S(1-f/m)^mn

приходим к формуле 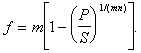(60)

Д) При наращивании по постоянной силе роста. Исходя из

S=Pe^dn

Получаем 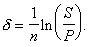(61)

Наращение по сложным процентам

Наращенная по сложным процентам сумма к концу срока ссуды с учетом падения покупательной способности денег (т.е. в неизменных рублях) составит

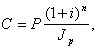(70)

где индекс цен определяется выражением (65) или (66), в зависимости от непостоянства или постоянства темпа инфляции.

В этом случае падение покупательной способности денег компенсируется при ставке i=h, обеспечивающей равенство C=P.

Применяются два способа компенсации потерьот снижения покупательной способности денег при начислении сложных процентов.

А) Корректировка ставки процентов, по которой производится наращение, на величину инфляционной премии.Ставка процентов, увеличенная на величину инфляционной премии, называется брутто-ставкой. Будем обозначать ее символом r. Считая, что годовой темп инфляции равен h, можем написать равенство соответствующих множителей наращения

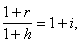(71)

где i - реальная ставка.

Отсюда получаем формулу Фишера

r=i+h+ih. (72)

То есть инфляционная премия равна h+ih.

Б) Индексация первоначальной суммы P. В этом случае сумма P корректируется согласно движению заранее оговоренного индекса. Тогда

S=PJ_p(1+i)ⁿ. (73)

Нетрудно заметить, что и в случае А) и в случае Б) в итоге мы приходим к одной и той же формуле наращения (73). В ней первые два сомножителя в правой части отражают индексацию первоначальной суммы, а последние два - корректировку ставки процента.