Определение параметров уравнения парной регрессии

Важнейший частный случай стат. связи – корреляционная связь. При корреляц. связи разным значениям одной переменной соответствуют различные ср. значения др. переменной, т.е. с изменением значения признака х изменяется ср. значение признака у.

В статистике принято различать след. виды зависимости:

4. парная корреляция – связь между 2^мя признаками результативным и факторным, либо м-ду двумя факторными.

5. частная корреляция – зависимость м-ду результативным и одним факторным признаком при фиксир. значении др. факторного признака.

6. множественная корреляция – зависимость результат. признака от двух и более факторных признаков.

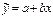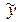Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид . Где - ср. значение разультативного признака y, при определеных значениях признака x; a – свободный член уравнения; b – коэф-фициент регрессии, показывает вариацию приз-нака y, приходящуюся на единицу вариации x.

Параметры уравнения находятся с помощью метода наименьших квадратов. Исходным методом наименьших квадратов для прямой линии является следующее:

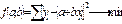
С помощью преобразований получаем систему нормальных уравнений:

an + båx_i=åy_i

aåx_i + båx_i²=åx_iy_i

Если первое уравнение системы разделить на n:

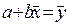, откуда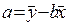

Для расчета параметра b используется формула:

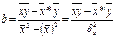Коэффициент парной регрессии, обозначенный b имеет смысл показателя силы связи между показателями факторного признака x и вариаций результативного признака y. Положительный знак при коэффициенте регрессии говорит о прямой связи между признаками, знак «-» говорит об обратной связи между признаками.

49. Множественное уравнение регрессии.Важнейший частный случай стат. связи – корреляционная связь. При корреляц. связи разным значениям одной переменной соответствуют различные ср. значения др. переменной, т.е. с изменением значения признака х изменяется ср. значение признака у. Множественная корреляция – зависимость результат. признака от двух и более факторных признаков. Матем. корреляц. зависимость результат. переменной от нескольких факторов опис-ся ур-нием множеств. регрессии: y(x₁,x₂…x_k)= a+b_1.2…kx₁+b_2.13…kx₂+….+b_k.12…k-1x_k Уравнение множеств. регрессии характ-т ср. изменение y с изменением признаков факторов. При построении уравнения множественной регрессии нужно решить две задачи: Выбрать признаки – факторы, включенные в регрессию. Выбрать тип уравнения регрессии. Решение 1-ой задачи основыв-ся на рассмотрении матрицы парных коэффиц-тов корреляции и выделении тех переменных, для которых выполняется правило: Ryx_j > Rx_iy_j (где i≠j). Кроме того, не рекоменд-ся включать во множеств. регрессию переменные, тесно связанные м-ду собой. Решение 2-ой задачи основыв-ся на соотношении: чем проще тип ур-ния множеств. регрессии, тем очевиднее интерпретация его параметров, тем лучше для использ-ния регрессии с целью анализа и прогноза. Параметры множеств. ур-ния регрессии так же, как и в парном уравнении регрессии расчитыв-ся методом наим. квадратов. å(y_i-a-b₁x₁-b₂x₂-…-b_kx_k)→min Получаем систему уравнений: an + b₁åx₁+ b₂åx₂+_…+ b_kåx_k =åy aåx₁ + b₁åx_i²+ b₂åx₁x₂+…+ b_kåx₁x_k =å yx₁ aåx_k + b₁åx₁x_k + b₂åx₂x_k+…+ b_kåx_k² =å yx_k Отсюда a= y(ср.) - å b_j x_j(ср.) Коэффиц-ты b_j наз-ся коэфф-ми условно чистойрегрессии. Термин условно-чистая регрессия означает, что каждая из величин 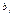измеряет среднее по совокупности отклонение результ. признака от его ср. величины на ед-цу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии не изменяются и не варьируют. Коэффициенты условно-чистой регрессии явл. именованными величинами, поэтому их преобразуют в сравнимые величины. Полученные показатели наз-т стандартизированными коэфф-ми регрессии ( 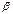- коэффициенты). β_j= b_j*σ_xj / σ_{y, где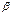} - коэффициенты показывают на ск-ко отклоняется от своего ср. значения в средних квадратических отклонениях результат. признак y при отклонении факт. признака 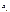от своего ср. значения на 1 среднее квадратическое отклонение. Коэффициенты эластичности показывают на сколько % изменится результ. признак при изменении факторного на 1%:Э_j= b_j*( x_j(ср.) / y_(ср.)) Коэффициент совокупной детерминации: R²=å Ryx_i β_i Важно знать вклад каждой объясняющей переменной, он измеряется коэффиц-ми раздельной детерминации: D_i²= Ryx_i β_i50.Частная и множественная корреляция.Поскольку на изучаемый результат. признак влият не один факторный признак, а множество, то возникает задача изолированного измерения тесноты связи результат. признака с каждым из признаков- факторов при элиминировании (погашении связи) др. признаков-факторов, а так же задача измерения тесноты связи между результат. признаками и всеми признаками-факторами, включенными в анализ. В анализ включ-ся те фактор. признаки, для кот. их корреляция м-ду собой слабее корреляции с результат. признаком. На основе коэф-тов парной корреляции можно рассчитать коэф-ты частной корреляции. Частная корреляция- чистая корреляция м-ду двумя переменными при погашении связи с др. переменными. Коэф-т частной корреляции первого порядка, когда погашается связь с одной переменной: 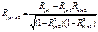Коэф-т частной корреляции второго порядка: 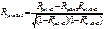Точка в подстрочных значках R означает погашение связи х₂ и х₃ с у и х₁. Коэф-ты частной корреляции принимают значения от -1 до 1. На основе коэф-тов частной корреляции расчит-ся коэф-ты частной детерминации. Он обозначается как R²(yx_k .x₁x₂…x_k-1x_k+1…x_m) Коэф-ты множественной детерминации показывает, какая часть дисперсии результат. переменной у объясняется за счет учтенных в анализе факторных признаков. Этот показатель обозначается R²(yx₁…x_k) и изменяется в интервале (0,1)

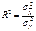, где 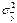-дисперсия переменной у, а 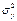- общая дисперсия переменной у. Извлекая корень квадратный из 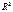получим коэф-т множеств. корреляции у. Он должен быть не < максимального из парных или частных коэф-тов корреляции. Назначение коэф-та множеств. корреляции состоит в оценке качества ур-ня множеств. регрессии: чем > значение R, тем ближе оно к 1, тем лучше уравнение регрессии, тем надежнее рез-ты анализа или прогноза на его основе.

51. Оценка результатов корреляционно-регрессионного анализа.Важн. частный случай стат. связи – корреляционная связь. При корреляц. связи разным значениям одной переменной соотв-ют различные ср. значения др. переменной. Задачей корреляц. анализа явл. колич. оценка тесноты связи м-ду признаками. Регрессия исследует форму связи. З-ча регресс. анализа – опр-ние аналитич. выражения связи. Коррел- регресс. анализ включает в себя измерение тесноты связи и установления аналитич. выражения связи.

Показатели корреляц. связи, вычисленные по ограниченной совок-ти явл-ся лишь оценками той или иной законом-ти, поскольку в любом параметре сохраняется эл-т случайности. Поэтому необх-ма стат. оценка ст-ни точности и надежности пар-ров корреляции и регрессии. Надежность- вероят-ть того, что значение проверяемого парам-ра ≠0 и не включ-т в себя величины противопол-х знаков. Вероятностная оценка пар-ров корреляции произв-ся по общим правилам проверки стат. гипотез. В частности путем сравнения оцениваемой величины со ср. случайной ошибкой оценки. Для коэффиц-та парной регрессии(b) ср. ошибка оценки вычисл-ся по формуле: 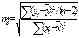где y^¯- знач-ния результ. признака, полученные по ур-нию регрессии; ∑(y_i-y¯)²/(n-2)- остат. дисперсия; (n-2)- число степеней свободы

Зная ср. ошибку оценки коэф. регресии м. вычислить вер-ть того, что нулевое значение коэфф-та входит в интервал возможных с учетом ошибки значений. С этой целью нах-ся отн-ние коэф. к его ср. ошибке, называемое t-критерий Стьюдента: t=b/m_b.

Если t расчетное > t табличного, то вероят-ть нулевого значения коэф. регрессии < ур-ня значимости (a) т.е. гипотезу о несуществовании этого коэфф-та можно отклонить. Надежность установленной связи м. проверить и по ср.случайной ошибке коэф. корреляции по фор-ле:

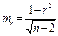
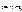Ср.ошибка условно чистого коэфф-та регрессии (b_j) рассчит-ся по формуле: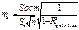

Sост.-остаточное ср. квадратич. отклонение результ. признака

;

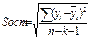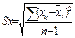
k- число ф-ров; n- ч-ло ед-ц совок-ти; i-№ ед-цы; j- номер ф-ра

Ср. ошибка оценки коэф-та множеств. корреляции по фор-ле: 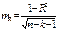Оценка рез-тов регресс. анализа начин-ся с оценки суммарной значимости рез-тов регресс. связи с пом. F-теста. Цель теста: выяснить объясняют ли х-переменные значимую часть вариации у. Если этот тест значим- связь сущ-т и можно приступать к ее ислед-нию и объяснению. F-тест выполняется с пом. компьют. программы и при опред-нии р-значения, т.е. значение доверит. вероят-ти того, что данные соотв-ют нулевой гипотезе. Нулевая гипотеза для F-теста утв-ет, что в генер. совок-ти м-ду х и у прогнозирующая взаимосвязь отсут-т. Если р-значение > 0.05, то полученный рез-т- незначительный, <–значимый, если <0.01-высокознач. Еще 1вариант основан на оценке коэф-та детерминации. Если R²< чем критич. значение по табл. R², то соотв. модель незначимая.После оценки значимости регресс. модели м. говорить, что значимы хотя бы 1или все коэф-ты регрессии.