WACC и изменения в структуре капитала

Менеджеры должны выбрать такую структуру капитала, которая делает максимальной цену данной фирмы. Однако оценить, как изменения структуры капитала повлияют на цену акции, довольно трудно. Модель оценки корпорации показывает, что ее операционная стоимость равна приведенной стоимости будущих потоков денежных средств при ставке дисконтирования, равной WACC (формула 17.5):

V= 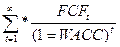(17.5)

Если у какой – либо фирмы нет неоперационных активов, стоимость операций будет также равна общей стоимости фирмы, а максимум ее стоимости может быть достигнут при такой структуре капитала, которая минимизирует WACC. Поскольку обычно легче предсказать, как какое – либо изменение структуры капитала повлияет на WACC,чем на стоимость акций, многие менеджеры при принятии решения об оптимальной структуре капитала руководствуются именно оценками WACC.

Если в структуре капитала фирмы нет привилегированных акций, то WACC рассчитывается следующим образом (формула 17.6):

WACC= 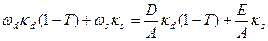(17.6)

В этом выражении D/A и E/A представляют доли долга (коэффициент левериджа) и акционерного капитала в активах (и пассивах) фирмы, и их сумма равна 1. Таблица 17.3 показывает ситуацию для компании М. Обратите внимание, что увеличение коэффициента левериджа увеличивает стоимость как заемного, так и акционерного капитала.

Таблица 17.3 . Оценка стоимости капитала и цены акций компании М при различных коэффициентах левериджа

Отношение D/A, %	Отношение D/Е, %	(1-Т)кd, %	Среднее значение EPS2	Оценка беты	Ks, %	Ожидаемая цена акции	Коэффициент PIE	Средневзвешенная стоимость капитала WACC, %
	0,00	4,8	2,40	1,50	12,0	20,00	8,33	12,00
	11,11	4,8	2,56	1,60	12,4	20,65	8,06	11,64
	25,00	5,0	2,75	1,73	12,9	21,33	7,75	11,32
	42,86	5,4	2,97	1,89	13,5	21,90	7,38	11,10
	66,67	6,0	3,20	2,10	14,4	22,22	6,94	11,04
	100,00	7,2	3,36	2,40	15,6	21,54	6,41	11,40
	150,00	9,0	3,30	2,85	17,4	18,97	5,75	12,36

На практике для того чтобы оценить, каким образом изменения левериджа повлияет на коэффициент текущей ликвидности, коэффициент покрытия текущих платежей по долгу и WACC, финансовые менеджеры применяют методы прогнозирования. Затем они обсуждают свои расчеты с представителями банков и рейтинговых агентств, которые сравнивают коэффициенты рассматриваемой фирмы с коэффициентами других фирм данной отрасли, и окончательно принимают решение о рейтинге облигаций и соответствующей процентной ставке.

Уравнение Хамады

Повышение коэффициента задолженности повышает также риск, которому подвергаются акционеры, и это оказывает влияние на стоимость акционерного капитала, k_s. Эту взаимосвязь трудно определить в цифрах, но ее можно оценить. Роберт Хамада вывел следующую формулу, определяющую влияние финансового левериджа на коэффициент бета собственного капитала компании (формула 17.7):

b=b_u[1+(1-T)(D/E)] (17.7)

Уравнение Хамады показывает, как увеличение коэффициента левериджа повышает бету собственного капитала. b_u обозначает коэффициент бета фирмы (и собственного капитала) без финансирования за счет заемных средств, т.е. ее коэффициент в случае, если фирма финансировалась исключительно за счет собственного капитала. Таким образом, бета b_u фирмы, не использующей заемных средств, полностью зависит от делового риска компании и, таким образом, является удобной ее мерой. С помощью простого преобразования формулы (17.7) можно легко выразить b_u через коэффициент левериджа и текущую бету (формула 17.8):

b_u= 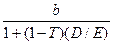(17.8)

Обратите внимание, что бета является единственной переменной в уравнении стоимости капитала к_s=k_RF+(k_M-k_RF)*b, которая бы находилась под контролем – хотя бы частичным – руководства фирмы. И k_RF и k_M определяются рыночными силами, которые находятся вне сферы влияния менеджмента фирмы. Однако на b оказывает влияние: 1) решение об организации операционной деятельности данной фирмы – они влияют на b_u; 2) решение фирмы по поводу структуры капитала, что отражается в ее коэффициентах D/A и E/A.

Мы можем проиллюстрировать формулу Хамады на примере фирмы М. Мы будем считать, что безрисковая ставка доходности k_RF равна 6%, а рыночная норма доходности k_M составляет 10%. Далее вспомним, что в настоящее время фирма не имеет задолженности (D/A = D /A=0), а ее ROE= к_s=12% (см. рис. 17.1.). Отсюда, используя формулу модели ценообразования капитальных активов, легко найти, что нынешний коэффициент бета фирмы равен:

b_u= b=( к_s- k_RF)/( k_M-k_RF)=(12-6)/(10-6)=1,5

На рис. 17.5. графически изображена требуемая доходность акционерного капитала к_s компании М при различных коэффициентах левериджа. Как показано на рисунке, к_s состоит из 6%-ой безрисковой доходности, премии за деловой риск, также равной 6%, и премии за финансовый риск, которая по мере роста задолженности возрастает с нарастающей скоростью.