Определение основных статистических характеристик

Статистический анализ в Excel

Выборочная функция распределения

Задание 1

Построить эмпирическое распределение результатов тестирования в баллах для следующей выборки: 69, 85, 78, 85, 83, 81, 95, 88, 97, 92, 74, 83, 89, 77, 93.

Решение

1. В ячейку А1 введите слова Результаты, в диапазон А2:А16 - результаты тестирования.

2. Выберите ширину интервала 5 баллов. Тогда при крайних результатах 69 и 97 баллов, получится 7 интервалов. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.

3. Введите заголовки создаваемой таблицы: в ячейку D1 – Абсолютные частоты, в ячейку Е1 – Относительные частоты, в F1 – Накопленные частоты.

4. Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек D2:D8, вызовите Мастер функций, категория – Статистические, функция – Частота, в поле Массив данных введите диапазон данных тестирования А2:А16, в поле Массив интервалов введите диапазон интервалов С2:С8, нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D8 появится массив абсолютных частот.

5. В ячейке D9 найдите общее количество результатов тестирования, с помощью Автосумма.

6. Заполните столбец относительных частот. В ячейку Е2 введите формулу =$D2/$D$9 .

Протягиванием скопируйте полученное значение в диапазон Е3:Е8. Получим массив относительных частот.

7. Заполните столбец накопленных частот. В ячейку F2 скопируйте значение относительной частоты из ячейки Е2. В ячейку F3 введите формулу =F2+E3. Протягиванием скопируйте полученное значение в диапазон F4:F8. Получим массив накопленных частот.

8. В результате получим таблицу, представленную на рисунке 1.

	A	B	C	D	E	F
	Результаты		Границы	Абсолютные частоты	Относительные частоты	Накопленные частоты
					0,067	0,067
3 д					0,067	0,133
					0,133	0,267
					0,333	0,600
					0,133	0,733
					0,200	0,933
					0,067	1,000

Рис. 1. Результат вычислений относительных и накопленных частот

9. Постройте диаграмму относительных и накопленных частот. Выделите диапазон Е1:F8, вызовите Мастер диаграмм, откройте вкладку Нестандартные, выберите тип диаграммы График/гистограмма2, нажмите Далее. Откройте вкладку Ряд и в поле Подписи оси Х выделите диапазон С2:С8, нажмите Далее. Откройте вкладку Заголовки, в поле Ось Х введите название Баллы, в поле Ось Y – Относительная частота, в поле Вторая ось Х – Накопленная частота. Нажмите Готово.

Получите диаграмму как на рисунке 2.

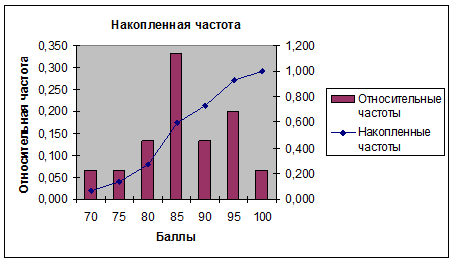
Рис. 2.Диаграмма относительных и накопленных частот

Задание 2

Для данных из задания 2 построить эмпирические распределения, воспользовавшись процедурой Гистограмма.

Решение

1. В ячейку А1 введите слова Результаты, в диапазон А2:А16 - результаты тестирования.

2. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.

3. Для вызова процедуры Гистограмма выберите меню Сервис – Анализ данных,выделите Гистограмма, нажмите Ok.

4. В окне Гистограмма в поле Входной диапазон введите диапазон исследуемых данных А2:А16, в поле Интервал карманов введите диапазон С2:С8, в поле Выходной диапазон введите ссылку на левую верхнюю ячейку выходного диапазона F1.

Установите переключатели в положение Интегральный процент и Вывод графика, нажмите Ok.

Сравните полученную диаграмму с диаграммой из задания 1.

Упражнения

1. Постройте эмпирические функции распределения успеваемости в группе из 20 студентов: 4, 4, 5, 3, 4, 5, 4, 5, 3, 5, 3, 3, 5, 4, 5, 4, 3, 5, 3, 5.

2. Постройте эмпирические функции распределения для роста (в см) группы из 20 мужчин: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181, 183, 172, 176.

Определение основных статистических характеристик

Задание 3

Найдите выборочные среднее, моду, дисперсию и стандартное отклонение для следующей выборки: 26, 35, 29, 27, 33, 35, 30, 33, 31, 29.

Решение

1. В диапазон А1:А10 введите данные выборки.

2. В ячейке А11 с помощью Мастера функций, категория Статистические, вычислите среднее значение – функция СРЗНАЧ.

3. В ячейке А12 вычислите наиболее часто встречающее значение в выборке, с помощью функции МОДА.

4. В ячейке А13 найдите дисперсию выборки, характеризующую степень разброса элементов выборки относительно среднего значения. Используйте функцию ДИСП.

5. В ячейке А14 найдите стандартное отклонение выборки от среднего значения, с помощью функции СТАНДОТКЛОН.

Задание 4

Для данных из задания 3 найдите основные статистические характеристики с помощью инструментов Пакета анализа.

Решение

1. В диапазон А1:А10 введите данные выборки.
2. Выберите в меню Сервис команду Анализ данных, выделите строку Описательная статистика, нажмите Ok.
3. В поле Входной интервал выделите диапазон А1:А10, активируйте переключателем поле Выходной интервал и укажите ячейку А11. В разделе Группировка, установите переключатель по столбцам. Установите флажок в поле Итоговая статистика и нажмите Ok.
4. В результате анализа в указанном выходном диапазоне получим соответствующие значения.

Медиана – число, которое является серединой выборки.

Эксцесс – частоты появления удаленных от среднего значения.

Асимметрия – величина, характеризующая несимметричность распределения элементов выборки относительно среднего значения. Принимает значение от -1 до 1. Для симметричного распределения асимметрия равна 0.

Интервал – разница между максимальным и минимальным значениями элементов выборки.

Счет – количество элементов в выборке.

Упражнения

В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (мг/м3): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Определите основные статистические характеристики с помощью Мастера функций и инструмента Описательная статистика.