Рассчитать параметры сетевого графика, а результаты расчетов свести в таблицу 1

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Московский государственный открытый университет

Имени В.С. Черномырдина

Кафедра «Промышленный менеджмент и логистика»

ЗАДАНИЕ

на выполнение курсовой работы

по предмету «Планирование производства»

для студентов

Тематика курсовых работ по дисциплине «планирование производства»

1.Прогнозирование экономической конъюнктуры, спроса и конкуренции в отрасли промышленности.

2.Прогнозирование долгосрочных тенденций научно-технического развития.

3.Обоснование важнейших показателей стратегического плана развития предприятия.

4.Планирование найма, подготовки и переподготовки кадров.

5.Планирование и регулирование средств на оплату труда персонала.

6.Планирование производства продукции на предприятии.

7.Планирование сбыта продукции производственно-технического назначения.

8.Планирование производственной программы вспомогательных и обслуживающих подразделений предприятия.

9.Планирование и управление программами научно-исследовательских и опытно-конструкторских работ.

10.Разработка финансового плана предприятия.

11 .Планирование внешнеэкономической деятельности предприятия.

12.Налоговое планирование на предприятии.

13.Планирование качества продукции на предприятии.

14.Планирование социального развития персонала предприятия.

15.Система бюджетов как инструмент планирования и контроля деятельности предприятия.

16.Сравнительная оценка эффективности источников финансирования инвестиционных решений.

17.Имитационное моделирование как метод обоснования плановых решений на предприятии

18.Разработка проекта организации системы планирования на предприятии.

19.Использование сценарного подхода как метода обоснования управленческих решений.

20.Использование теории игр в обосновании управленческих решений.

21.Использование экспертных методов в планировании производственно-хозяйственной деятельности предприятия.

22.Оценка риска и неопределённости в инвестиционных решениях.

23. Построение «дерева» целей как метода обоснования плановых решений.

24.Применение «дерева» решений в обоснования планов предприятия.

25.Решение проблемы многокритериального выбора управленческих альтернатив в планировании.

26. Планирование маркетинговой деятельности предприятия.

27. Использование теории управления запасами в организации планирования и контроля на предприятии.

28. Использование методов анализа иерархий в практике планирования.

29. Использование методов математического программирования в практике планирования.

30. Применение платежной матрицы в практике планирования.

31 .Организация системы оперативного планирования производства.

32.Обоснование плановых решений, направленных на повышение эффективности производства (снижение себестоимости продукции, повышении производительности труда, рентабельности производства)

33. Использование метода «Дельфи» в практике планирования.

34. Использование теории массового обслуживания в практике планирования.

ЗАДАНИЕ

на выполнение курсовой работы

Рассчитать параметры сетевого графика, а результаты расчетов свести в таблицу 1.

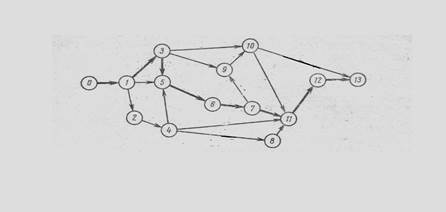
Вариант
Событие	Продолжительность работы
ti	tj	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j
		21	19	20	21	20	19	19	20	21	21	20	20	19	21	19
		13	14	13	13	14	12	13	12	14	13	13	14	12	12	14
		26	27	28	28	26	28	27	26	26	26	26	28	27	26	26
		36	34	33	35	36	33	33	34	36	34	36	34	35	33	35
		5	8	6	7	6	8	7	5	8	6	7	5	6	7	5
		15	13	12	12	15	14	14	13	13	15	13	12	14	14	12
		16	15	13	13	16	14	15	13	16	14	14	15	13	13	16
		19	20	22	21	19	19	22	21	22	22	19	21	20	22	19
		9	8	6	7	9	6	6	8	6	8	7	7	8	7	6
		15	13	16	16	13	15	13	14	15	13	15	16	16	15	14
		39	41	40	42	39	39	39	41	40	39	42	40	41	39	42
		47	48	50	48	50	47	49	50	48	50	47	49	49	47	50
		33	36	34	34	35	33	36	34	33	36	35	36	34	33	35
		29	28	28	28	29	27	27	28	29	29	27	27	27	29	28
		65	68	67	67	70	65	68	67	68	70	65	67	68	65	67
		8	6	9	6	7	7	7	9	9	7	6	6	8	6	7
		13	15	12	15	12	12	14	13	13	12	15	13	14	12	13
		12	13	15	14	13	15	13	14	15	13	12	14	14	13	15
		16	15	13	15	16	14	15	15	13	14	16	14	15	13	16
		43	41	40	41	43	43	42	41	40	42	43	42	41	40	40
		48	47	50	50	47	49	49	50	48	49	48	50	47	47	48
Продолжение таблицы
Вариант
Событие	Продолжительность работы
ti	tj	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j	ti-j
		19	19	20	21	20	19	21	21	20	20	21	21	19	19	21
		13	13	14	14	12	14	13	12	13	13	12	14	14	13	12
		28	26	27	27	28	28	27	27	26	27	26	28	26	27	28
		34	35	35	33	33	36	33	35	33	35	34	33	33	36	36
		8	6	7	5	8	7	8	6	5	8	5	6	6	5	8
		15	12	14	15	12	15	14	13	15	14	12	13	14	13	15
		13	16	14	13	16	13	15	14	16	15	16	13	14	14	15
		20	19	20	20	19	22	19	21	21	20	20	22	21	21	19
		9	8	8	9	7	9	6	9	7	8	6	6	7	7	8
		14	15	15	16	13	15	14	16	14	15	13	14	16	16	14
		40	41	41	39	39	39	41	40	39	41	42	42	40	42	41
		48	47	48	47	48	49	49	50	48	49	48	47	47	50	49
		35	33	33	36	35	34	35	35	33	36	35	34	33	34	36
		28	29	27	29	29	29	28	27	27	28	29	28	28	28	27
		65	70	65	65	68	70	68	70	68	67	67	68	65	70	68
		8	6	9	8	6	8	9	7	8	7	8	8	9	9	9
		15	12	14	15	12	14	14	13	13	15	14	12	14	13	15
		15	14	12	13	14	12	15	12	13	14	15	15	14	12	14
		16	14	13	15	16	13	13	14	14	15	15	15	14	13	16
		43	40	41	41	43	42	40	43	41	42	41	40	43	41	42
		50	48	49	50	48	49	47	48	47	49	49	48	50	47	47

Методические указания к выполнению курсовой работы

Рассмотрим построение сетевой модели на условном примере.

К основным параметрам сетевого графика относятся критиче­ский путь, резервы времени событий и резервы времени работ. Эти параметры являются исходными для получения ряда дополнитель­ных характеристик, а также для анализа сети или, что тоже самое, для анализа составленного плана разработки.

На графике (см. рис.1) критический путь изображен жирной линией. Изменение продолжительности любой работы, лежащей на критическом пути, соответствующим образом меняет (сокращает или удлиняет) срок наступления завершающего события. Свойства, присущие работам критического пути, а также возможности, кото­рые открываются при использовании этих свойств, в значительной мере и определяют эффективность сетевых графиков.

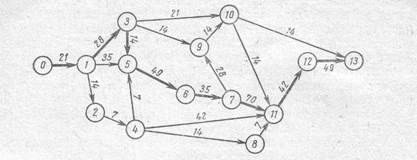
Рис.1. Сетевой график для комплекса работ по проектированию и изготовлению стенда

При планировании комплекса операций критический путь по­зволяет найти срок наступления завершающего события. В процессе правления ходом разработки внимание руководителей должно быть сосредоточено на главном направлении — на работах критического пути. Это позволяет наиболее целесообразно и оперативно контролировать ограниченное число работ, влияющих на срок работки, а также лучше использовать ресурсы (людей и сред­ства).

В некоторых случаях в сетевом графике может быть не один, а несколько критических путей, имеющих одинаковую продолжительность, большую, чем продолжительность других путей.

В сетевых графиках имеются и другие пути, опирающиеся на исходное и завершающее события (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с ним. Эти пути, по продолжительности меньшие крити­ческого пути, называются ненапряженными. Ненапряженные пути обладают важным свойством: на участках, не совпадающих с кри­тической последовательностью работ, они имеют резервы времени. Это означает, что задержка в выполнении работ и свершении собы­тий, не лежащих на критическом пути, до определенного момента (до исчерпания располагаемых резервов) не влияет на сроки завер­шения разработки в целом. Критические пути резервами не рас­полагают. Если свершение какого-либо события, находящегося на критическом пути будет задержано, то либо будет отодвинуто на тот же срок свершение завершающего события, либо должны быть сокращены на такое же в сумме время продолжительности работ, расположенных на критическом пути после этого события (цепочка последующих работ). Таким образом, если даже удастся обеспечить соблюдение установленного срока свершения завершающего собы­тия при затяжке в выполнении какой-либо из работ критического пути, то это будет достигнуто за счет переоценки времени выпол­нения других работ или ускорения сроков их выполнения, а не за счет резервов у работ или событий критического пути.

Из ненапряженных путей наибольший интерес представляют подкритические пути — ближайшие по продолжительности к кри­тическому, а также наименее напряженные.

Подкритические пути могут стать критическими в результате сокращения продолжительности работ, лежащих на критическом пути; таким образом, они потенциально опасны с точки зрения соблюдения сроков завершения разработки и входят наряду с работами и событиями критического пути в критическую зону.

Наименее напряженные пути не представляют угрозы для нару­шения директивных сроков окончания работ и поэтому могут рассматриваться как резерв с точки зрения использования ресурсов (рабочей силы, денежных средств), выделенных для их выполнения. Перераспределение этих ресурсов с передачей их на работы крити­ческого пути может привести к сокращению продолжительности последнего и, таким образом, приблизить срок свершения завер­шающего события.

Резервы времени существуют в сетевом графике во всех случаях, когда имеется более одного пути разной продолжительности. Величину резервов времени должны внимательно анализировать руководители комплекса работ.

Резерв времени события — это такой промежуток времени, на который может быть отсрочено свершение этого события без нару­шения сроков завершения разработки в целом.

Резерв времени события R_i- определяется как разность между поздним T_пi и ранним Т_рi. сроками свершения события i:

R_i = T_пi - T_рi , (1)

Наиболее поздний из допустимых сроков T_пi — это такой срок свершения события, превышение которого вызовет аналогичную задержку наступления завершающего события. Иными словами, если событие наступило в момент T_пi , оно попало в критическую зону и последующие за ним работы должны находиться под таким же контролем, как и работы критического пути.

Наиболее ранний из возможных сроков свершения события Т_рi.— срок, необходимый для выполнения всех работ, предшествующих данному событию. Это время находят, выбирая максимальное зна­чение из продолжительностей всех путей, ведущих к данному событию.

Можно следующим образом сформулировать правило определе­ния Т_р и Т_пдля любого события сети: ранний срок и поздний срок свершения события определяют по максимальному из путей, прохо­дящих через данное событие, причем Т_р равно продолжительности максимального из предшествующих данному событию путей, а Т_п является разностью между продолжительностями критического пути и максимального из последующих за данным событием путей.

Максимальный путь, ведущий к событию i, обозначается L_1i, а наибольший по продолжительности путь, следующий за собы­тием i →L_2i.Тогда в соответствии с приведенными выше прави­лами определения ранних и поздних сроков свершения события

T_рi = t(L_1i)_; (2)

T_пi = t (L_кр) – t (L_2i)_; (3)

а для критического пути

t (L_1i) + t (L_2i) = t (L_кр) (4)

Следовательно, для событий, принадлежащих критическому пути, T_pi = Т_пi. Иными словами, события критического пути имеют нулевой резерв времени, т.е. для этих событий наибольший допустимый срок равен наименьшему ожидаемому. Путь, соединяющий эти события, соответствует максимальной продолжительности последовательных работ, ведущих от исходного к завершающему событию. Исходное и завершающее события во всех случаях имеют нулевой резерв времени. Таким образом, наиболее простой способ выявления критического пути — это определение всех последовательно расположенных событий, имеющих нулевой резерв времени. Такой способ наиболее эффективно использовать при автоматизации расчетов.

Для некоторых разработок устанавливается директивный срок свершения завершающего события, который может быть меньше рассчитанного по сетевому графику на основании оценок, данных ответственными исполнителями. В последнем случае некоторые события могут иметь отрицательные резервы времени. Критический путь будет проходить через события с наибольшими по абсолютной величине отрицательными резервами. Этот случай далее не рассмат­ривается, так как находится в противоречии с одной из основных предпосылок СПУ, заключающейся в том, что оно основано на пла­нировании снизу, а не на установлении волевых сроков сверху.

Расчет ранних и поздних сроков свершения событий рассмотрен на примере сетевого графика, изображенного на рис.1. Результаты расчета сведены в табл.1.

Расчет начинается с первой работы 0-1. Чтобы перейти от собы­тия 0 к событию 1, следует ко времени свершения события 0 (кото­рое в данном случае равно нулю) прибавить 21 день, потребный для выполнения работы, приводящей к событию 1. Других путей между событиями 0 и 1 нет, поэтому значение 21 заносится в графу T_pj (табл.1).

Таблица 1

Параметры сети Предшест­вующее событие i Последующее событие j tожij Tpj Tпj Rj Rпij Rcij

Чтобы определить время свершения события 2, ко времени свер­шения события 1 (равному 21 дню) прибавляют время выполнения работы 1-2 (14 дней). Полученное время (T_р2 = 35 дням) заносят в графу T_рj таблицы. Те же логические рассуждения позволяют определить время свершения события 3 (к 21 дню прибавляется 28 дней выполнения работы 1-3, т. е. T_рi3 — 49), а также события 4 - Т_р2 = 35 дням плюс время для выполнения работы 2-4 (7 дней), т. е. 42 дня.

Как следует из графика сети, событию 5 предшествуют две работы. Событие 5 не может совершиться до выполнения всех ведущих к нему работ, и поэтому ранним сроком его свершения Т_Р5, будет максимальное время, т. е. 63 дня.

Дальнейшие расчеты T_Pj пояснений не требуют. Весь ход вычис­лений сводится, таким образом, к следующим расчетам:

T_Pl + T_0-I= 21;

T_P2= T_Pl+ T_l-2= 35;

T_P3 = T_Pl + t_l-3 = 49;

Т_Р4 = T_P2 + t_2-4= 42;

T_Р5 = mах [T_Р1 + t_1-5; T_P3 + t_3-5; T_p4 + t_4-5] = T_р3 + t_3-5= 63

и т. д. до завершающего события:

T_Р13 = mах [T_Р10+ t_10-13; T_Р12+ t_12-13] = T_Р12+ t_12-13 = 308.

Результаты вычислений сведены в табл.1.

Итак, ранний срок свершения завершающего события равен 308 дням.

При определении позднего срока свершения событий Т_писходят из того, что для завершающего события величина T_пcравна раннему сроку свершения этого события T_pc. Такая предпосылка следует из сформулированных выше понятий раннего и позднего сроков свер­шения события и из того, что завершающее событие лежит на критическом пути, а следовательно, имеет нулевой резерв времени (T_pc = T_пc).

Величина Т_п определяется последовательно для каждого собы­тия сети; при этом расчет Т_п ведется от завершающего события к исходному.

Таким образом, установив, что для события 13 время Т_п = Т_р, в графу T_пj следует внести значение 308. Чтобы получить Т_п пред­шествующего события, следует вычесть ожидаемое время работы t_12-13 из последующего события. Тогда T_п13c составит 308—49 = 259 дней.

Пользуясь аналогичными рассуждениями, находят значение T_п11, равное 217 дням. Все работы, предшествующие событию 11, должны быть завершены не позднее 217-го дня, считая от начала выполне­ния комплекса работ; соответственно в графу T_пjтаблицы вносят значения Т_п, относящиеся к работам 10-11; 7-11; 4-11 и 8-11.

Расчет T_п10 выполняется иначе. Событие 10 представляет узел расходящихся работ. За ним следует работа .10-11 продолжительностью 14 дней (Т_п10 = 217—14 = 203 дня); есть и другой путь от события 10 — через работу 10-13. Так как T_п13 = 308 дням, а время работы 10-13 равно. 14 дням, T_п10 = 294 дням. В таких случаях следует выбирать наименьшую из полученных величин, поскольку, выбрав только наиболее раннюю дату, обеспечивают необходимое время для достижения завершающего события по самому длинному пути.

В самом деле, если принять Т_п для события 10 не меньшее (203 дня), а большее (294 дня), то достижение завершающего собы­тия по пути 10-11, 12-13 будет возможно только через 399 дней (294 + 14 + 42 + 49 = 399), а не через 308 дней, как было уста­новлено ранее.

Дальнейший ход вычислений Т_п показан ниже:

Т_п13 = 308; Т_п12 = Т_п12 - t_12-13 = 259;

Т_п11= Т_п12 - Т_11-12 = 217;

T_п13 = min [T_п13+ t_10-13; T_п11+ t_10-11] = T_п11+ t_10-11= 203;

Т_п9= Т_п10- t_9-10 =189;

Т_п8= Т_п11– t_8-11= 210;

Т_п7 = min [T_п11+ t_7-11; T_п9+ t_7-9] = T_п11+ t_7-11 = 147;

и т. д. до события I и исходного события 0:

Т_п1 - min [Т_п2 - t_1-3; Т_п5 - Т_1-5; Т_п2– t_1-2] = Т_п3– t_1-3= 21;

Т_п0 = Т_п1– t_0-1 =0.

Правильность расчетов подтверждается полученным значением Т_п для исходного события, равным нулю. Только в этом случае вели­чина критического пути будет равна ранее вычисленной, т. е. 308 дням. Результаты расчетов Т_птакже занесены в табл.1.

Зная Т_п и Т_р для всех событий, определяют резервы времени событий по формуле (2):

R₁ = Т_п1 - T_Pl = 21 - 21= 0;

R₂ = Т_п2 - T_p1 = 49 - 35 = 14;

R₃ = Т_п3 - T_p3 = 49 - 49 = 0;

R₄ = Т_п4 - T_p4 = 56 - 42 = 14

и т. д. Наибольший резерв времени имеет событие 8:

R₈ = Т_п8 - T_p8 = 210 - 56 = 154.

Как указывалось, критический путь проходит через события с нулевым резервом времени, т. е. через события 0—1—3—5—6—7— 11—12—13.

Резервами времени располагают не только события, но и пути (кроме критического, как уже отмечалось выше), а также работы, лежащие на некритических путях.

Для определения резерва времени пути следует вернуться к тому условию, что длина критического пути в сетевом графике больше, чем длина любого другого полного пути.

Разница между длиной критического пути t (L_Kp) и длиной любого другого пути t (L_i) называется полным резервом времени пути L_i.

Этот резерв R (L_i) обозначается

R (L_i) = t (L_кр) - t (L_i) (5)

Полный резерв пути показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих пути L_i иными словами, — предельно допустимое увеличение продолжительности этого пути. При дальнейшем увеличении пути L_i (или, что тоже самое, при дальнейшем затягивании выполнения работ, лежащих на этом пути) критический путь переместится с ранее вычисленной последовательности работ на последователь­ность работ пути L_i. Отсюда можно сделать вывод, что любая из работ пути на участке, не совпадающем с критическим путем, обла­дает резервом времени.

Резерв времени работы определяется посредством резерва вре­мени пути, на котором находится эта работа. Следует при этом учитывать, что работа может принадлежать нескольким путям одно­временно. Например, работа 1-2 (см. рис.1) принадлежит сразу че­тырем путям. Один из них идет по последовательности 0—1—2—4— 5—6—7—9—10—11—12—13, второй — по пути 0—1—2—4—5—6— 7—11—12—13, третий 0—1—2—4—11—12—13, четвертый 0—1—2— 4—8—11—12—13. Ясно, что полный резерв времени этой работы не может быть больше, чем резерв времени максимального из путей, проходящих через эту работу. Если это условие не будет выполнено, т. е. если полный резерв времени работы будет исчислен не по максимальному пути, то использование всей его величины (а она будет, естественно, больше, чем величина полного резерва, вычисленная по максимальному пути) задержит всю разработку и сместит срок наступления завершающего события. Отсюда вытекает также, что резерв времени пути может быть распределен между отдельными работами, находящимися на этом пути, только в пре­делах полных резервов времени этих работ.

Важным свойством полного резерва времени работы является то, что если его использовать частично или целиком для увеличе­ния длительности какой-либо работы, то соответственно уменьшится резерв времени всех остальных работ, лежащих на этом пути. При использовании полного резерва времени работы целиком для одной работы резервы времени остальных работ, лежащих на мак­симальном пути, проходящем через эту работу, будут полностью исчерпаны, поскольку полный резерв времени работы принадлежит не одной работе, а всем работам, лежащим на путях, проходящих через эту работу. Резервы времени работ, лежащих на других (не максимальных) путях, проходящих через эту работу, сократятся и будут равны разности между прежним резервом времени этих работ и использованным полным резервом времени работы, лежащей на максимальном пути.

Полный резерв времени работы R_nij определяется по формуле

R_nij = T_nj - T_pi -t_ij (6)

где i — начальное событие данной работы; j - конечное событие этой работы.

Например, для работы 1-2 (см. рис.1) полный резерв вре­мени работы будет равен (пользуемся данными табл.1, где уже вычислены резервы времени событий) R_п1-2 = 49 – 21 - 14 = 14 дней.

Свободный резерв времени R_сi-j равен разности между ранними сроками наступления событий j и i за вычетом продолжительности работы (i-j):

R_ci-j = T_pj - T_pi -t_ij . (7)

Свободный резерв времени — это максимальное количество времени, на которое можно увеличить продолжительность отдельной работы, не изменяя при этом ранних сроков начала последующих работ при условии, что непосредственно предшествующее событие наступило в свой ранний срок. В этом смысле свободный резерв — это независимый резерв. Его использование на какой-либо работе не меняет величины свободных резервов остальных работ сети, так как при его исчислении в качестве плановых сроков начала вы­полнения всех работ приняты ранние сроки наступления со­бытий.

Все рассчитанные данные о резервах работ также отражены в табл.1.

Зная ранние и поздние сроки свершения событий, можно для любой работы определить также и ранние и поздние сроки начала и окончания работы. Самый ранний из возможных сроков начала работы

T_рнi-j = T_pi (8)

Самый поздний из допустимых сроков начала этой работы

R_пнij = T_пj-t_ij (9)

Самый ранний из возможных сроков окончания работы

T_роij = T_Pi + t_lij (10)

и, наконец, самый поздний из допустимых сроков окончания работы

T_поij = T_пj (11)

Например, самый ранний срок окончания работы 10-11 будет Т_ро10-12= 189 + 14 = 203 дня, тогда как следующая работа 11-12 не может начаться ранее чем через 217 дней (так как это ранний срок свершения события 11).

Резервы времени работы позволяют маневрировать сроком начала работы, ее продолжительностью, сроком окончания. Нет резервов — нет возможности маневрирования: так обстоит дело с работами критической зоны. Именно поэтому на эти работы и должно быть обращено в основном внимание руководителей.

Наличие резервов обязывает к правильному их использованию. Процесс оптимизации сетевых графиков в значительной мере связан с использованием резервов времени работ.

На рис.2 представлена графическая интерпретация воз­можностей использования пол­ного и свободного резервов вре­мени работ. На этом графике ось абсцисс является осью вре­мени, поэтому все построения вдоль этой оси, в том числе про­должительность работы i-j, даются в соответствующем масштабе.

Полный резерв времени ра­боты может быть распределен, как отмечалось, между рабо­тами, находящимися на пути, которому принадлежит данная работа. При этом и начальное, и конечное события этой работы могут располагать резервами времени.

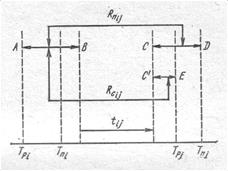Рис.2. Образование свободного резерва времени

Графически полный резерв может быть представлен как сумма двух отрезков АВ + CD. Каждый из этих отрезков охватывает величину резерва времени соответствующего события R_i и R_j и величину возможного смещения начала или окончания работы. Эти последние величины зависят, естественно, от продолжитель­ности самой работы.

Свободный резерв — это резерв собственно работы i-j при усло­вии свершения предшествующего и последующего событий в их ранние сроки. Свободный резерв определяется суммой отрезков АВ и C'F.

Действительно, как указывалось, аналитическое выражение свободного резерва определяется выражением T_pj — T_pi— t_ij. Изображенные на рис.2 отрезки соответствуют величине этого выражения.

Ответственные исполнители, располагая графиками, характе­ризующими резервы закрепленных за ними работ, могут представить возможности маневрирования ресурсами времени.