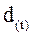Операции наращения и дисконтирования в

Инвестиционном анализе

Логика построения основных алгоритмов достаточно понятна и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы (PV) с условием, что через некоторое время t будет возвращена сумма FV. Эффективность подобной сделки может быть охарактеризована одной из двух величин:

темп прироста:

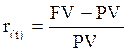; [8.2]

темп снижения:

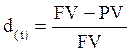. [8.3]

В финансовых расчётах первый показатель ( 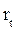) имеет ещё название «процент», «рост», «ставка процента», «норма доходности», а второй – «дисконт», «ставка дисконтирования», «коэффициент дисконтирования». Очевидно, что обе ставки взаимосвязаны:

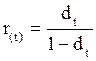; или .

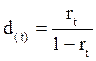Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берётся за базу сравнения: в формуле (8.2) – исходная сумма, в формуле (8.3) – возвращаемая сумма.

Итак, в любой простейшей финансовой сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.

Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом наращения или компаундинга. Процесс, в котором задана возвращаемая сумма и коэффициент дисконти-рования, называется процессом дисконтирования. В первом случае речь идёт о движении денежного потока от настоящего к будущему, во втором – о движении от будущего к настоящему (см. рис. 19).

Экономический смысл финансовой операции, задаваемой формулой (8.2), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции.

Поскольку из формулы (8.2)

,

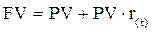и 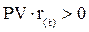, то можно наглядно представить, что время генерирует деньги.

Будущее

Наращивание

Процентная ставка r(t)

Возвращаемая сумма (FV)

Исходная сумма (PV)

Настоящее

Возвращаемая сумма (FV)

Приведенная сумма (исходная) (PV)

Дисконтирование

Дисконтная ставка

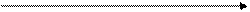
Рис. 19. Логика финансовых операций

На практике норма доходности является величиной непостоянной, зависящей главным образом от степени риска, ассоциируемого с данным видом бизнеса, в который инвестирован капитал (чем выше степень риска, тем выше норма доходности). К примеру, наименее рискованными являются вложения в государственные ценные бумаги или в Госбанк, однако норма доходности в этом случае относительно невысока.

Коэффициент дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. При этом искомая величина (PV) показывает как бы текущую, «сегодняшнюю» стоимость будущей величины (FV).

Дисконт, связанный с суммовыми величинами (формула 8.3), исполь-зуется главным образом в операциях по учёту векселей банком, т. е. в том случае, если владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его, т. е. купить, удерживая в свою пользу часть вексельной суммы, нередко также называемой дисконтом. В этом случае банк предлагает владельцу сумму (PV), исчисляемую исходя из объявленной банком ставки дисконтирования ( 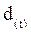). Расчёт этой суммы ведётся по формуле, вытекающей из формулы 8.3:

;

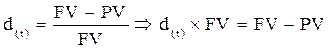
тогда

.

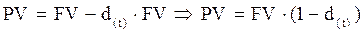[8.4]

К примеру, векселедержатель предъявил для учёта вексель на сумму 10 тыс. грн. со сроком погашения 15.04.2000 г. Вексель предъявлен 31.03.2000г. Банк согласился учесть вексель с дисконтом в 65 % годовых. Тогда дисконтная ставка на 15 дней составит (15/360)·0.65=0,027083. Следовательно, сумма, которую векселедержатель может получить от банка, рассчитывается по формуле (8.4):

PV=10 · (1 – 0,027083) = 9,72917 тыс. грн.

Комиссионные, удерживаемые банком в свою пользу за предоставленную услугу, в данном примере составили разницу между FV и PV или 270 грн. 83 коп.

FV–PV=10–9,72917=0,27083 тыс. грн.

Стандартным временным интервалом в финансовых операциях является 1 год. Существует две основные схемы наращения капитала:

схема простых процентов;

схема сложных процентов.

Если исходный инвестируемый капитал равен P, а требуемая норма доходности за 1 год – r (как коэффициент в долях единицы от начальной суммы Р), тогда считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину (P·r). Таким образом, размер инвестиционного капитала через n лет Pn будет равен:

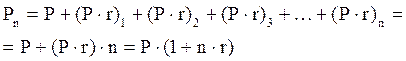. [8.5]

Если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты, то в этом случае инвестиция сделана на условиях сложного процента. В этом случае размер инвестированного капитала будет равен:

к концу первого, второго и n-ного года:

.

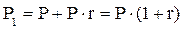
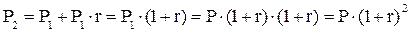
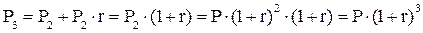
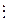
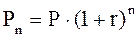[8.6]

Инвестирование на условиях сложного процента более выгодно, т. к.

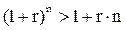или Pn на условиях простого процента меньше Pn на условиях сложного процента при n > 1.

В первом случае, при применении простого процента, доходы, по мере их начисления, целесообразно снимать для потребления или новой инвестиции, а во втором случае, при использовании сложного процента, инвестированный капитал непрерывно генерирует доходы и постоянно возрастает и не возникает объективная необходимость изъятия начисленных процентов для использова-ния в других инвестиционных проектах.

Формула 8.6 является базовой в финансовых вычислениях. Для удобства пользования ею значения факторного множителя (FM), обеспечивающего наращение стоимости, табулированы для различных значений r и n. При пользовании такими таблицами формула 8.6 имеет вид:

,

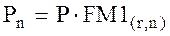
где 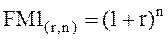– факторный множитель, экономический смысл кото-рого состоит в следующем: он показывает, чему будет равна одна денежная единица (1 гривня, 1 доллар и т. п.) через n периодов при заданной процентной ставке r на каждый из этих периодов.

Схема простых процентов используется в практике банковских расчётов при начислении процентов по краткосрочным ссудам (со сроком погашения до 1 года).

К примеру, выдана ссуда в размере 10 тыс. грн. на один месяц (30 дней) под 130 % годовых. Тогда размер платежа к погашению составит:

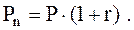
Норма доходности в долях единицы составит 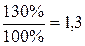на один год (360 дней). На 30 дней норма доходности должна составить ,

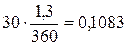где 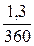– норма доходности на один день:

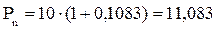тыс. грн.

В практике вложений нередко используются внутригодовые процентные начисления, т. е. при выплате дивидендов на вложенный капитал нередко оговаривается не только величина годового процента, но и частота выплаты в течение года. В этом случае расчет ведётся по формуле сложных процентов по подинтервалам и по ставке, равной пропорциональной доле исходной годовой ставки:

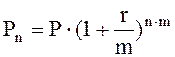, [8.7]

где m – количество начислений в году,

n – период реализации инвестиций, лет.

К примеру, в банковский депозит вложены деньги в сумме 10 тыс. грн. на 2 года с полугодовыми начислениями процентов под 20 % годовых. В этом случае начисление процентов производится 4 раза (2 раза в год в течение 2 лет) по ставке 10 % на полугодие (20 % : 2).

Если воспользоваться формулой 8.7, то сумма к концу двухлетнего периода составила бы:

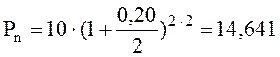тыс. грн.,

где 0,20/2 – норма доходности в долях единицы в расчёте на одно полугодие.

Можно сделать вывод, что чем чаще начисляются проценты, тем большая будет итоговая сумма при использовании формулы сложных процентов (т. е. в этом случае 12 % годовых не эквивалентны 1 % в месяц, а несколько больше при помесячном их начислении по формуле сложных процентов).

Наращение суммы к исходной инвестиции (вложению) происходит различными темпами в зависимости от частоты начисления процентов, причём с возрастанием частоты накопления сумма увеличивается.

Максимально возможное наращение реализуется при бесконечном дроблении годового интервала.

Так как

,

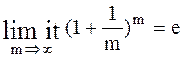(это важнейшая постоянная математического анализа, относящаяся к группе замечательных пределов – трансцендентное число e = 2,718281, одновременно является основанием натурального логарифма).

Тогда:

.

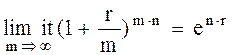В пределах одного года при непрерывном начислении процентов можно использовать формулу (n = 1):

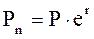. [8.8]

Возможности использования в контрактах на инвестиции (вложения) различных схем начисления процентов определяют объективную потребность и необходимость сравнительного анализа эффективности таких вложений с использованием некого универсального показателя для любой из схем начисления.

В сравнительном анализе эффективности вложений используют показатель эффективной годовой процентной ставки 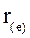, обеспечивающий переход от P к Pn при заданных значениях этих показателей.

В рамках одного года, исходя из формулы 8.7, такой переход реализуется зависимостью:

.

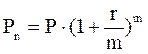Тогда по определению эффективной процентной ставки:

.

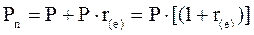Приравняв эти формулы, получим:

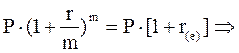
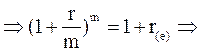
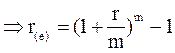. [8.9]

Можно сделать вывод, что эффективная годовая ставка зависит от количества внутригодовых начислений, с ростом которых она также увеличивается.

К примеру, у частного предпринимателя есть возможность получить ссуду на разных условиях:

1) на условиях ежеквартального начисления процентов из расчёта 80% годовых;

2) на условиях полугодового начисления процентов из расчёта 85 % годовых.

Чтобы выяснить, какой вариант более предпочтителен, необходимо рассчитать относительные расходы предпринимателя по обслуживанию ссуды, величина которых оценивается эффективной годовой процентной ставкой. Чем она ниже, тем более предпочтителен вариант (относительные расходы самые маленькие):

;

.

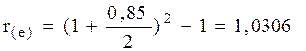Из расчётов следует, что второй вариант является более предпочтительным.

У предпринимателя всегда есть выбор, куда вложить свободные денежные средства. Такой выбор всегда является выбором того вида бизнеса, вложение средств в который принесёт максимальный доход. При оценке целесообразности таких вложений исходят из того, явится ли такое вложение более прибыльным (при допустимом уровне риска), чем вложения в государственные ценные бумаги, или наоборот, т. е. анализируют будущие доходы при минимальном («безопасном») уровне доходности.

Для этого используют несложные математические методы, основная идея которых заключается в оценке будущих поступлений P_n (в виде прибыли, процентов, дивидендов) с позиции текущего момента.

Для этого используется формула:

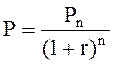, т. к. 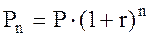, [8.10]

где 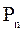– доход, планируемый к получению в n-м году;

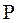– текущая (приведенная) стоимость (оценка величины дохода 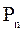с позиции текущего момента);

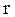– коэффициент дисконтирования.

То есть прогнозируемая величина 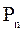через n лет с позиции текущего момента будет меньшей и равной Р. Темп снижения прогнозной стоимости до текущего момента задаётся величиной знаменателя формулы, и, прежде всего, величиной процентной ставки. В этом случае коэффициент дисконтирования равен процентной ставке, устанавливаемой инвестором, т.е. тому относитель-ному размеру дохода, который инвестор хочет или может получить на инвестируемый им капитал. Определяя коэффициент дисконтирования, обычно исходят из так называемого безопасного или гарантированного уровня рентабельности финансовых инвестиций, который обеспечивается государственным банком по вкладам или операциях с ценными бумагами.

К примеру, предприниматель имеет на счете в банке 40 тыс. грн. Банковский процент на вклад – 25 % годовых. Предприниматель получает предложение войти своим капиталом в организацию предприятия. Представленные предпринимателю расчёты показывают, что через 7 лет его капитал возрастёт в 4 раза ( 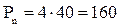тыс. грн.).

Для того чтобы ответить на вопрос, следует ли согласиться с предложением, необходимо сравнить две суммы: получаемая в результате вложения в предприятие и в банковское учреждение. Первая сумма составляет 160 тыс. грн. Вторая рассчитывается по формуле:

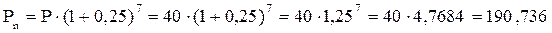тыс. грн.

С предложением соглашаться не следует. Однако, даже в случае принятия положительного решения по результатам счёта (т. е. если доход от вложения капитала выше дохода от вложения в банк) необходимо учесть фактор риска.