Прием относительных величин

Экономические явления и процессы, исследуемые в финансовом анализе, имеют, как правило, количественную определенность, которая выражается в абсолютных величинах. Абсолютные величины отражают количественные размеры явлений в единицах меры, веса, объема, протяженности, площади, стоимости и т.д. (тонны, метры, квадратные метры и т. д.) безотносительно к размеру других явлений.

Некоторые абсолютные величины могут иметь несколько единиц измерения. Объемы производства тканей могут измеряться в погонных метрах и квадратных метрах, стекла – в квадратных метрах и тоннах и т. д. В экономике кроме физических единиц измерения используются и условные (условно-натуральные) единицы измерения, которые применяются для сравнения объемов однородной, но разнокачественной продукции. Они применяются, например, в топливной промышленности для перевода различных видов топлива в т.н. условное топливо, в консервной – для перевода продукции в тысячи условных банок (тубы) и т.п.

Таким образом, использование абсолютных величин в финансовом анализе ограничено и имеет ряд недостатков, что обуславливает необходимость применения относительных величин.

Относительные величины представляют собой частное от деления одной величины на другую, которая принимается за базу сравнения.

Наиболее распространенными относительными величинами являются приведенные ниже в таблице 2.1.

Таблица 2.1. Виды относительных величин

Вид	Алгоритм расчета	Назначение
Относительная величина планового задания (прогноза, бюджета)	Отношение планового уровня показателя текущего года к фактическому его уровню в прошлом году или к среднему за три-пять предыдущих лет	Оценка напряженности планового задания (прогноза, бюджета)
Относительные величины выполнения плана (прогноза, бюджета)	Отношение фактического уровня показателя к его плановому уровню	Контроль за выполнением плана (прогноза, бюджета)
Относительные величины динамики	Отношение величины показателя отчетного периода к его уровню в предыдущем периоде	Характеризуют развитие явления во времени
Относительные величины структуры	Отношение части к целому	Характеризуют долю (удельный вес) отдельных частей совокупности
Относительные величины координации	Соотношение частей целого между собой	Характеризуют соотношение между отдельными частями совокупности
Относительные величины интенсивности	Отношение размера признака к объему среды	Характеризуют интенсивность распространения изучаемого признака
Относительные величины эффективности	Отношение эффекта к ресурсам (затратам)	Характеризуют результативность процессов и явлений

Прием относительных величин предполагает использование в анализе процентов, коэффициентов и индексов для получения дополнительной характеристики абсолютных значений изучаемых показателей.

Проценты используются для характеристики соотношения величин, одна из которых принимается равной 100. Кроме процентов (%) могут использоваться промилле (‰), если за базу сравнения берется 1 000 и продецимилле (‰о), если база составляет 10 000.

Коэффициенты используются для характеристики соотношения величин, одна из которых принимается равной единице, а вторая – за соответствующее отношение к единице.

Индекс – это относительный показатель, который получается при соотношении двух величин: отчетной и базисной (уровень, с которым сравнивается отчетная величина), выражающий изменения сложного экономического явления во времени, в пространстве или по сравнению с планом.

По сути, значение индексов для исследования экономических процессов и явлений настолько велико, что часто авторы выделяют прием, основанный на применении системы индексов, в самостоятельный прием финансового анализа и среди наиболее широко применяемых индексов используют приведенные ниже в таблице 2.2.

Таблица 2.2. Виды общих индексов

Вид	Алгоритм расчета	Назначение
Индекс стоимости товарной продукции	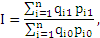где qi1 и qi0 – физический объем производства i-го вида про­дукции соответственно в отчетном и базисном периоде, рi1 и рi0 – це­на i-го вида продукции соответственно в отчетном и базисном периоде	Разность между числителем и знаменателем отражает изменение стоимости продукции в отчетном периоде по сравнению с базисным
Индекс физического объема		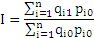Разность между числителем и знаменателем отражает изменение стоимости продукции за счет изменения физического объема
Индекс цен (индекс Пааше)		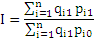Разность между числителем и знаменателем отражает изменение стоимости продукции в результате изменения цен
Индекс цен (индекс Ласпейреса)		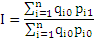Разность между числителем и знаменателем отражает изменение стоимости продукции в результате изменения цен

На практике кроме перечисленных выше применяется большое количество других индексов.

Прием средних величин

Прием средних величин предполагает использование средних показателей, которые представляют собой обобщающую характеристику качественно однородных, но количественно отличных друг от друга величин. Средние величины позволяют выявить общую тенденцию, преобладающее направление развития процесса или явления. Заменяют большое число значений признака одной усредненной величиной.

Исходные данные и содержание исчисляемого показателя предопределяют вид используемой средней. В финансовом анализе используют различные виды средних величин, которые делятся на два больших класса:

• степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая, средняя кубическая);

• структурные средние (мода, медиана).

В финансовом анализе находят применение все виды средних величин, наиболее важные из которых представленны ниже в таблице 2.3.

Таблица 2.3. Виды средних величин, применяемых в финансовом анализе

Вид средней величины	Алгоритм расчета	Назначение
Средняя арифметическая простая	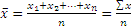, где x – индивидуальные значения признака; n – количество признаков в совокупности	Применяется в том случае, когда общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность
Средняя арифметическая взвешенная	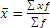, где f – частота признака	Применяется в том случае, когда варианты исследуемой совокупности встречаются неодинаковое количество раз
Средняя гармоническая простая		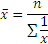Используется в тех случаях, когда произведение (xf) одинаково или равно 1
Средняя гармоническая взвешенная		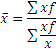Используется в тех случаях, когда известны индивидуальные значения признака и произведение признака на частоту (xf), а сами частоты неизвестны
Средняя геометрическая простая		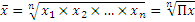Используется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин
Средняя геометрическая взвешенная	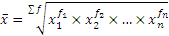, где f – промежуток времени между датами	Применяется для характеристики средних темпов роста в рядах динамики с неравноотстоящими уровнями
Средняя хронологическая простая		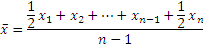Используется в тех случаях, когда имеющиеся данные относятся к фиксированным моментам времени c равными интервалами
Средняя хронологическая взвешенная		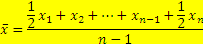Используется в тех случаях, когда имеющиеся данные, относятся к неравноотстоящим датам
Средняя квадратическая простая		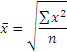Применяется, когда возникает потребность расчета среднего размера признака, выраженного в квадратных единицах измерения, для несгруппированных данных
Средняя квадратическая взвешенная		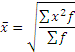Применяется, когда возникает потребность расчета среднего размера признака, выраженного в квадратных единицах измерения, для сгруппированных данных
Мода	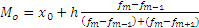, где х0 – нижняя граница интервала; h – величина интервала	Для определения наиболее часто встречающегося варианта ряда
Медиана		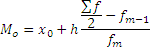Для определения значения признака, который лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части

При использовании средних величин в АХД следует учитывать, что всякая средняя величина нивелирует, взаимопогашает положительные и отрицательные явления, что может привести к неверным выводам о состоянии отдельного объекта анализа в общей совокупности.

Группировки

Группировка – это прием выделения качественно однородных групп по характерным признакам (группировка предприятий по численности работников, по объемам произведенной продукции и т. д.). Группировки позволяют не только систематизиро­вать материал, но и выявлять характерные и типичные взаимо­связи процессов, гасить случайные отклонения. В качестве группировочного признака необходимо выбирать такой признак, который позволяет раскрыть природу изучаемых явлений, их сущность.

Группировки делятся на 3 вида: типологические, структурные, аналитические (таблица 2.4).

Таблица 2.4. Классификация группировок

Вид группировки	Назначение
Типологические	Позволяют выделить типы социально-экономических процессов и явлений (например, группы населений по роду деятельности, группы предприятий по формам собственности и др.)
Структурные	Оценка внутреннего строения показа­телей (например, классификация персонала по стажу работы, по профессиям и др.)
Аналитические	Определение наличия, формы и направления связи между изучаемыми показателями (напри­мер, изучение зависимости суммы выданного банком кредита от величи­ны процентной ставки)

Кроме того, группировки могут быть простыми и сложными. С помощью простых группировок изучается взаимосвязь между явлениями, сгруппированными по какому-либо одному признаку. В комбинированных группировках такое деление изучаемой совокупности производится сначала по одному признаку, а потом внутри каждой группы – по другому признаку и т.д. Таким образом могут быть построены двух-, трех- и т.д. уровневые группировки, которые позволяют изучить разнообразные и сложные взаимосвязи.

Графический прием

Графический прием – это представление экономических процессов и явлений в виде графиков, которые являются масштабным изображением показателей, чисел с помощью геометрических фигур (линий, прямоугольников, окружностей и т.п.) или условно-художественных фигур. Они имеют большое иллюстративное значение. Благодаря им изучаемый материал становится более доходчивым и понятным.

Основные формы графиков, которые используются в анализе – диаграммы. Диаграммы по форме представления информации бывают столби­ковые, полосовые, круговые, линейные, пузырьковые и др.

По содержанию различают диаграммы сравнения, структурные, динамические, графики связи, графики контроля и т.д.

Диаграммы сравнения показывают соотношения разных объектов по какому-либо показателю. Наиболее простым и наглядным графиком для сравнения величин показателей яв­ляются столбиковые и полосовые диаграммы. Для их состав­ления используют прямоугольную систему координат. На оси абсцисс размещают основу столбцов одинакового размера для всех объектов. Высота каждого столбца должна быть сораз­мерна величине показателя, который нанесен в соответствен­ном масштабе на ось ординат. Полосовые диаграммы размещают по горизонтали: ос­нову полос размешают на оси ординат, а масштаб — на оси аб­сцисс.

Иногда диаграммы сравнения представляют в виде квадра­тов или кругов, площадь которых пропорциональна величине соответствующих показателей,

Особой разновидностью являются фигурные диаграммы, в которых соотношения объектов показываются в виде ус­ловно-художественных фигур (колоса, клубня, головы жи­вотного, трактора и т.д.).

Структурные (секторные) диаграммы позволяют выразить состав изучаемых показателей, удельный вес отдель­ных частей в общей величине показателя. В структурных ди­аграммах изображение показателя дастся в виде разбитых на сектора геометрических фигур (квадратов, кругов), площадь ко­торых берется за 100 или 1. Величина сектора определяется удельным весом части.

Диаграмма динамики предназначена для иллюстрации из­менения явлений за соответствующие промежутки времени. Для этой цели могут использоваться столбиковые, круговые, но чаще – линейные графики. Динамика на таком графике представляется в виде линии, которая характеризует беспрерывность процесса. Для построения линейных графиков пользуются системой коорди­нат: на оси абсцисс откладывают периоды, а на оси ординат – уровень показателей за соответствующие отрезки времени, ис­ходя из принятого масштаба.

Линейные графики очень широко используются при изу­чении связей между показателями (графики связи). На оси аб­сцисс откладываются значения факторного показателя (X), а на оси ординат – значения результативного показателя (Y) в со­ответствующем масштабе. Линейные графики в наглядной форме отражают направление и форму связи.

Графики контроля находят широкое применение в АХД при изучении сведений о ходе выполнения плана. В таком слу­чае на графике будут две линии: плановый и фактический уро­вень показателей за каждый день или другой промежуток вре­мени.

Графический прием может использоваться также при решении методических задач АХД и в первую очередь при построении разнообразных схем для наглядного изображения внутреннего строения изучаемого объекта, последовательности технологических операций, взаимосвязей между результативными и факторными показателями и т.д.

Балансовый прием

Балансовый прием – отраже­ние соотношений, пропорций двух групп взаимосвязанных и уравновешенных экономических показателей, итоги которых должны быть тождественными. Он широко используется при анализе обеспеченности предприятия трудовыми, финансовыми ресурсами, сырьем, топливом, материалами, основными средствами производства и т.д., а также при анализе полноты их использования.

Самым типичным примером увязки большого числа показателей финансово-хозяйственной деятельности организации путем выведения двух групп взаимосвязанных и равных итогов является бухгалтерский баланс, который представляет собой равенство актива (средств организации) и пассива (источников их образования).

Определяя, например, обеспеченность предприятия материальными ресурсами составляют баланс, в котором, с одной стороны, отражается потребность в сырье, материалах, топливе и т.п., а с другой – фактическое их наличие.

При анализе использования трудовых ресурсов сравнивают возможный фонд рабочего времени с фактическим количеством отработанных часов, определяют причины сверхплановых потерь рабочего времени.

Для определения платежеспособности предприятия составляется платежный баланс, в котором соотносятся платежные средства с платежными обязательствами организации.

Т.о., в анализе применяются модели, построенные на основе товарного баланса, баланса трудовых ресурсов, платежного баланса и др. Например,

Он + П = Р + В + Ок, (2.4)

где О_н – остаток товаров на начало отчетного периода,

П – поступление товаров,

Р – реализация товаров,

В – другие направления использования товаров,

О_К – остаток товаров на конец отчетного периода.

Используя приведенный выше товарный баланс, можно определить любой из неизвестных показателей при известных остальных. Например,

Р = Он + П - В - Ок, (2.5)

В некоторых случаях балансовый прием может быть использован для определения величины влияния отдельных факторов на прирост результативного показателя или для проверки полноты и правильности определения влияния различных факторов на изменение результативного показателя. Например, когда из трех факторов известно влияние двух, то влияние третьего (∆Y₃) можно определить, отняв от общего прироста результативного пока­зателя (∆Y) результат влияния первых двух факторов (∆Y₁ и ∆Y₂):

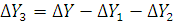(2.6)

В последнем случае в экономической литературе такой прием часто называют сальдовым.