Расчет значений потока платежей

Годы	Начальные инвестиции (1С) и чистые денежные потоки, тыс. руб. (РР,)	Коэффициенты достоверности	Начальные инвестиции и чистые денежные потоки, скоррек­тированные на коэффи­циенте достоверности, (тыс. руб.) (а х СГ,)	Дисконтный множитель при ставке коэффициент (1 + г)-'	Современная стоимость денежных потоков, тыс. руб. (гр. 1 х гр. 4)	Современная стоимость денежных потоков, скорректирован­ная на коэффи­циенте досто­верности, тыс. руб. | Д а, х СР{ |
Показатель
I ( = 1 (1 + г)' ]'-(гр. 3 х гр. 4)
А
	-100 000	1,00	-100 000	1,00	-100 000	-100 000
	50 000	0,90	45 000	0,909091	45 455	40 909
	60 000	0,80	48 000	0,826446	49 587	39 669
	60 000	0,70	42 000	0,751315	45 079	31 555
NРV					+40 121	+12 133

Как видно из табл. 65, чистая приведенная величина скорректи­рованного с учетом риска потока платежей меньше обычной суммы на 27 988 тыс. руб. (40 121 - 12 133), или в 3,3 раза.

Данный метод не предполагает увеличения риска с постоянным коэффициентом при сохранении простоты расчета, что позволяет учи­тывать риск более корректно.

Анализ чувствительности критериев эффективности (NPV, Р/и др.) сводится к исследованию зависимости результативного показателя от вариации значений составляющих его показателей. Анализ предусматри­вает выполнение ряда операций. Сначала задается взаимосвязь между исходными и результативными показателями в виде математического уравнения:

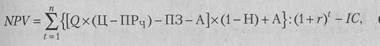(163)

где Q — количество продукции;

Ц — цена за единицу продукции; ПР_Ч — переменные расходы на единицу продукции; ПЗ — постоянные затраты; А — амортизация; Н — налог на прибыль.

Далее определяются наиболее вероятные значения исходных по­казателей и возможные диапазоны их изменений. Затем значения ис­ходных показателей меняются и определяется их влияние на конеч­ный результат. Анализ чувствительности критериев эффективности предполагает использование приема элиминирования (когда меняет­ся один из исходных показателей, в то время как значения остальных остаются постоянными). Проект с меньшей чувствительностью NPV считается менее рисковым.

К недостаткам метода относится изменение одного исходного по­казателя, в то время как остальные считаются постоянными. На практи­ке между показателями существует взаимосвязь и изменение одного из них приводит к изменениям остальных. Кроме того, метод не по­зволяет получить вероятностные оценки возможных отклонений исход­ных и результативного показателей.

Метод сценариев позволяет провести исследование чувствитель­ности результирующего показателя и анализ вероятных оценок его отклонений. Анализ инвестиционных рисков данным методом выпол­няется следующим образом. Определяют несколько вариантов изме­нений ключевых исходных показателей (пессимистический, наиболее

вероятный и оптимистический). По каждому варианту изменений экс­пертным путем устанавливают его вероятностную оценку. Для каждого варианта рассчитывают вероятное значение критерия NPV. Определяют среднюю величину NPV по формуле

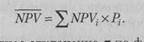(164)

Исчисляют стандартное отклонение а по формуле

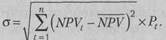(165)

Определяют коэффициент вариации (V) по формуле

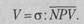(166)

На основании этих расчетов проводится оценка риска проекта.

Пример 22.

Рассматривается инвестиционный проект, связанный с выпуском изде­лия А. Полученные в результате опроса экспертов сценарии его реализации и возможные вероятности их осуществления приведены в табл. 66. Необходи­мо провести анализ риска проекта.

Таблица 66 Сценарии реализации проекта по производству изделия А

Показатели	Обозначение	Сценарии
наихудший с вероят­ностью 0,25	вероятный с вероят­ностью 0,5	наилучший с вероят­ностью 0,25
Объем выпуска, шт.	Q
Цена за штуку, руб.	Ц
Переменные расходы, руб.	ПРЧ
Постоянные затраты, руб.	ПЗ
Амортизация, руб.	А
Налог на прибыль, %	Н
Норма дисконта, %	г
Срок проекта, лет	п
Начальные инвестиции, руб.	1С	2 000	2 000	2 000
Чистые денежные поступ­ления, руб.	NCF,	212,5	1 350	2 487,5

По данным табл. 66 определяют значение NPV по вариантам, используя формулу

NPV=NCF_txa_n._r-IC,

где а„. _г — коэффициент приведения годовой ренты;

по наихудшему сценарию:

NPV- 212,5 х 4,564 - 2000= -1030,2 руб.;

по вероятному сценарию:

NPV= 1350x3,791 -2000 = 3117,9 руб.;

по наилучшему сценарию:

NPV= 2487,5 х 3,993 - 2000 = 7932,6 руб.

Далее определяется среднее ожидаемое значение NPV:

NPV= -1030,2 х 0,25 + 3117,9 х 0,5 + 7932,6 х 0,25 = 3284,55 руб.

Затем исчисляется стандартное (среднее квадратическое) отклонение:

a = V(-1030,2-3284,55)²x0,25 + (3117,9-3284,55)²x0,5 + + (7932,6-3284,55)²х0,25 = 3173,2руб.

Таким образом, исходя из предположения о нормальном распределе­нии случайной величины с вероятностью около 80% можно утверждать, что значение NPV будет находиться в диапазоне 3284,6 ± 3173,2 руб.

Для определения степени риска инвестиционного проекта исчис­ляется коэффициент вариации (V):

V= 3173,2 руб.: 3284,6 руб. = 0,97.

Полученные результаты в целом свидетельствуют о небольшом уровне риска для данного проекта. Среднее значение NPV (3284,6) не­намного выше прогноза экспертов (3117,9 руб.) и больше стандартно­го отклонения (3173,2 руб.). Значение коэффициента вариации (0,97) меньше 1, следовательно, риск данного инвестиционного проекта ниже среднего риска инвестиционного портфеля организации.

В том случае, если значение стандартного отклонения и коэффи­циента вариации по этому проекту меньше, чем по другим проектам, при прочих равных условиях ему следует отдать предпочтение.

Пример 23.

Рассматриваются два взаимоисключающих проекта, требующих одина­ковых первоначальных инвестиций в сумме 3600 тыс. руб. и рассчитанных на реализацию в течение 5 лет. Стоимость капитала для предприятия составляет

10%. Менеджеры определили три сценария ежегодных поступлений денеж­ных средств от каждого из проектов. Исходные данные и результаты расчетов приведены в табл. 67.

Таблица 67 Исходные данные и результаты вероятностного анализа

Показатели	Вероятность осуществ­ления	Проект А	Проект Б
Инвестиции, тыс. руб.		3 600	3 600
Сценарии ежегодного поступления денежных средств:
пессимистический		1 000
наиболее вероятный		1 200	1 500
оптимистический	1 500	2 000
Оценка NPV по сценарию:
пессимистическая	0,25		-567
наиболее вероятная	0,5		2 086
оптимистическая	0,25	2 086	3 982
Среднее NPV	1 044	1 897
Стандартное отклонение, s			1 774
Коэффициент вариации, V		0,65	0,94

Проект Б с большим значением стандартного (среднего квадратического) отклонения и коэффициентом вариации считается более рисковым.

В целом метод сценариев позволяет получить достаточно убеди­тельные результаты для различных вариантов реализации проектов, информируя о чувствительности, а также о возможных отклонениях выбранного критерия эффективности проектов.

Вместе с тем метод исследует поведение только результирующих показателей эффективности (NPV, IRR, РТ), не давая информации о возможных отклонениях потоков денежных поступлений и других ключевых показателях, определяющих процесс реализации проекта.

Несмотря на некоторые ограничения, метод успешно применяет­ся во многих разделах финансового анализа.

Анализ вероятностных распределений потоков предполагает опре­деление ожидаемой величины чистых поступлений наличности (NCF_t) в соответствующем периоде, расчет чистой современной стоимости

(NPV) и оценку ее возможных отклонений. Проект с наименьшей ва­риацией доходов считается менее рисковым.

Проблема заключается в том, что количественная оценка вариа­ции зависит от степени корреляции между отдельными элементами потока платежей.

В реальной практике между элементами потока платежей суще­ствует умеренная корреляция. В этом случае вычисления существен­но усложняются, необходимы специальные программные продукты.

В целом применение этого метода анализа рисков позволяет полу­чить информацию об ожидаемых значениях NPV и чистых поступле­ниях, а также их вероятностных распределениях.

Использование этого метода предполагает, что вероятности для ; всех вариантов денежных поступлений известны или могут быть точ­но определены. В действительности распределение вероятностей мо­жет быть задано с высокой степенью достоверности только на основе анализа больших объемов фактических данных. Чаще всего такие дан­ные недоступны, поэтому распределения, по оценкам экспертов, от­личаются субъективизмом, а расчеты на их основе — определенной условностью.

Дерево решений обычно используется для анализа рисков проек­тов, имеющих обозримое или разумное число вариантов развития. Они ценны в ситуациях, когда решения, применяемые в граничные момен­ты времени (t = и), зависят от предыдущих решений и в свою очередь определяют сценарии дальнейшего развития событий.

Анализ инвестиционных рисков данным методом выполняется следующим образом.

Для каждого момента времени определяют проблему и все возмож­ные варианты дальнейших событий, откладывают на дереве решений соответствующую вершину и исходящие от нее дуги, каждой дуге при­писывают ее денежную и вероятностную оценки, исходя из значений всех вершин и дуг рассчитывают вероятное значение критерия NPV (IRR, РГ). Далее проводят анализ вероятностных распределений полу­ченных результатов. Проекты с большей ожидаемой величиной NPV являются предпочтительными.

Вместе с тем с ростом числа периодов реализации проекта струк­тура дерева решений сильно усложняется, требует сложных вычисле­ний, а также применения специальных программных средств для реа­лизации моделей.

Преодолеть многие недостатки перечисленных методов позволяет имитационное моделирование — наиболее мощное средство анализа экономических систем.

Имитация — это компьютерный эксперимент с моделью системы, а не с самой системой.

При решении многих задач финансового анализа используются модели, содержащие случайные величины, поведение которых не под­дается управлению (со стороны лиц, принимающих решения). Такие модели называют стохастическими, а имитацию — методом Монте-Карло. Применение имитации позволяет сделать выводы о возмож­ных результатах, основанных на вероятностных распределениях слу­чайных факторов.

Имитационное моделирование рисков инвестиционных проектов предусматривает серию численных экспериментов, дающих эмпири­ческие оценки степени влияния различных факторов (объема выпуска, цены, переменных расходов и др.) на зависящие от них результаты.

Имитационный эксперимент выполняется следующим образом. Устанавливается взаимосвязь между входными и выходными пока­зателями (NPV, IRR, PI) в виде математического уравнения или нера­венства, задаются законы распределения вероятностей для ключевых параметров модели, проводится компьютерная имитация значений ключевых параметров модели, рассчитываются основные характери­стики распределений входных и выходных показателей, проводится анализ полученных результатов.

Результаты имитационного эксперимента можно дополнить ста­тистическим анализом, а также использовать для построения прогноз­ных моделей и сценариев.