Коэффициенты (темпы) роста
СОДЕРЖАНИЕ
Введение................................................................................................ 4
Рекомендации по оформлению контрольной работы............................... 4
Методические указания по выполнению задач........................................ 5
Варианты контрольной работы............................................................... 23
Контрольные вопросы по курсу............................................................ ..42
Примерные тесты к экзамену (зачету)..................................................... 43
Библиографический список.................................................................... 60
ВВЕДЕНИЕ
Целью изучения студентами курса "Статистика: общая теория" является приобретение навыков в области методологии статистического анализа экономической информации. Статистика служит инструментом в работе экономистов высшей квалификации: менеджеров, бухгалтеров, аудиторов, финансистов и др.
В результате изучения дисциплины студенты должны:
· знать принципы и методы сбора статистической информации;
· владеть методикой ее обобщения;
· выполнять статистический анализ данных;
· уметь интерпретировать полученные результаты и обоснованно формулировать выводы.
РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа выполняется с целью закрепления и проверки знаний, полученных студентами в процессе самостоятельного изучения учебного материала, а также для выявления их умения применять на практике методы статистики.
Приступая к осуществлению работы, необходимо ознакомиться с соответствующими разделами курса, изучить рекомендованную литературу, уделить особое внимание методике построения и технике расчета и анализа статистических показателей.
К выполнению контрольной работы предъявляются следующие требования:
1) работа выполняется в рукописном или печатном вариантах, обязательно приводится номер задания, текст условия задач;
2) решение следует начинать с теоретического обоснования и приведения необходимых формул;
3) расчеты должны быть развернутыми, содержать пояснения;
4) если возможны несколько методов расчета того или иного показателя, следует применять наиболее простой из них, указав при этом и другие способы решения;
5) проверка правильности выполнения расчетов должна осуществляться на основе взаимосвязи показателей с учетом их экономического содержания;
6) все записи следует делать разборчиво, используя лишь общепринятые сокращения слов;
7) расчет относительных величин следует производить с точностью до 0,001 (до 0,1%);
8) при необходимости решения задач оформляются с использованием статистических таблиц и графиков, которые следует строить в соответствии с правилами, принятыми в статистике;
9) по результатам расчетов должны быть сделаны краткие выводы;
10) страницы работы должны быть пронумерованы; для замечаний рецензента оставляются поля. После рецензирования необходимые исправления выполняются в конце работы после рецензии;
11) в заключении работы необходимо привести список использованной литературы, поставить свою подпись и указать дату выполнения.
Вариант заданий выбирается в соответствии с начальной буквой фамилии студента:
| Начальная буква фамилии студента | Номер варианта |
| А, Б, В | |
| Г, Д, Е, Ж, 3 | |
| И, К, Л, М | |
| Н, О, П, Р | |
| С, Т, У, Ф, Х | |
| Ц, Ч, Ш, Щ, Э, Ю, Я |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЗАДАЧ
Задача 1предполагает освоение студентами важнейшего статистического метода изучения взаимосвязей общественных явлений - аналитических группировок.
На основе аналитической группировки определяют наличие и направление связи между изучаемыми признаками. Группировка строится по факторному признаку, оказывающему влияние на связанные с ним результативные признаки. Число выделяемых групп определяется в соответствии с условием конкретной задачи. При группировке с равными интервалами величина интервала определяется по формуле
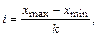
где 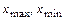 - соответственно, наибольшее и наименьшее значения группировочного признака в совокупности;
- соответственно, наибольшее и наименьшее значения группировочного признака в совокупности;
к - число выделяемых групп.
Например, по данным задачи 1 (вариант 1), величина интервала составит:
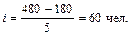
Каждая из выделенных групп характеризуется показателями, соответствующими условиям задач. Результаты группировки оформляются в виде статистической таблицы. Например, макет групповой таблицы задачи 1 (вариант 1) будет иметь следующий вид:
Группировка предприятий отрасли по среднегодовой стоимости
основных фондов и объему продукции
| Группа предприятий по среднегодовой стоимости основных фондов, млн. руб. | Число предприятий | Среднегодовая стоимость основных фондов, млн. руб. | Объем продукции, млн. руб. | Фондоотдача, руб. | ||
| всего | в среднем на 1 предприятие | всего | в среднем на 1 предприятие | |||
| А |  |  | 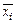 | 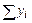 | 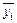 | 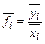 |
| Итого | 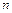 | 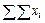 | 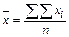 | 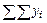 | 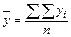 | 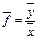 |
По результатам группировки необходимо сделать вывод о том, как с изменением факторного признака по выделенным группам изменяются значения результативного признака.
Выполнение задачи 2 позволит студентам овладеть методикой расчета относительных величин плана, реализации плана, динамики, структуры, сравнения, интенсивности, координации.
Задачи 3-4 предполагают вычисление средних величин по формулам средней агрегатной, средней арифметической и средней гармонической.
Выбор формулы расчета должен согласовываться с логическим свойством средних величин, т.е. должен быть обоснован экономически. Если по отдельным единицам совокупности известны объемный и количественный показатели (числитель и знаменатель логической формулы), то используют агрегатную среднюю; если известны количественный и качественный показатели, то используют среднюю арифметическую взвешенную; если известны объемный и качественный показатели, расчет производится по формуле средней гармонической взвешенной.
При расчете средней величины в интервальном ряду распределения необходимо определить середину каждого интервала как среднюю арифметическую простую из его границ. Величина открытых интервалов (где указана только одна, нижняя или верхняя, граница) условно принимается равной величине соседнего закрытого интервала. Далее расчет осуществляется по формуле средней арифметической взвешенной
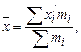
где 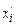 - середины интервалов;
- середины интервалов;
т - число повторений значений признака.
Следует иметь в виду, что в качестве веса отдельных вариантов могут быть использованы не только абсолютные значения частот, но и относительные - частости (доли, проценты к итогу).
Колеблемость признака в совокупности характеризуют показатели вариации:
· среднее линейное отклонение определяется как средняя из абсолютных значений отклонений отдельных вариантов от их средней величины:
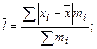
· среднее квадратическое отклонение рассчитывается как корень квадратный из дисперсии. Дисперсия представляет собой среднюю из квадратов отклонений отдельных вариантов от их средней величины:
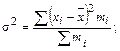
· коэффициент вариации определяется по формуле
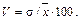
Модой в статистике называют значение признака, которое наиболее часто встречается в изучаемой совокупности. Для интервального ряда распределения значение моды определяется приближенно по формуле
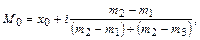
где х0 - нижняя граница модального интервала, т.е. интервала, которому соответствует наибольшая частота (частость);
i - величина модального интервала;
m2 - частота или частость модального интервала (наибольшая в ряду распределения);
m1 - частота или частость модального интервала, предшествующая модальному;
m3 - частота или частость интервала, следующего за модальным.
Медиана - значение признака, расположенное в середине ранжированного ряда распределения. Половина единиц совокупности имеет значение признака больше медианы, другая половина - меньше. Для интервального ряда распределения значение медианы рассчитывается по формуле
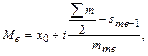
где х0 - нижняя граница медианного интервала (медианный - первый интервал, накопленная частота которого превысила половину общей суммы частот);
i - величина медианного интервала;
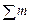 - сумма всех частот ряда;
- сумма всех частот ряда;
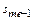 - сумма частот, накопленных до медианного интервала;
- сумма частот, накопленных до медианного интервала;
m - частота медианного интервала.
Аналогично медиане определяются децили - структурные средние, отделяющие в совокупности десятые части. Дециль первого порядка отделяет 10% единиц с наименьшими значениями признака, дециль девятого порядка - соответственно, 10% единиц с наибольшими значениями:
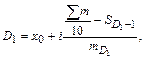

Децильный коэффициент дифференциации рассчитывается отношением децили девятого порядка к децили первого порядка.
Пример решения задачи 3
Имеются следующие данные по трем зерновым хозяйствам за два года:
| Хозяйство | Базисный год | Отчетный год | ||
| Урожайность зерновых, ц/га | Посевная площадь, га | Урожайность зерновых, ц/га | Валовой сбор зерна, ц | |
| х | m | х | М | |
| 19 000 | ||||
| 46 000 | ||||
| 36 000 |
Определите среднюю урожайность зерновых в базисном и отчетном годах.
Решение
Логическая формула для вычисления средней урожайности представлена уравнением:
Урожайность (х)= Валовой сбор (М) / Посевная площадь (m).
Поскольку посевные площади в хозяйствах различаются по размеру, следует использовать в расчете средней урожайности формулы взвешенных средних.
Для базисного периода следует использовать среднюю арифметическую взвешенную, так как известны количественный (посевная площадь) и качественный (урожайность) показатели:
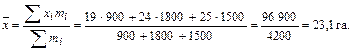
В отчетном периоде известны качественный и объемный показатели, поэтому используем формулу средней гармонической взвешенной:
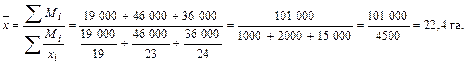
Следовательно, в отчетном году получен валовой сбор на 4100 ц (101 000-96 900) больше, чем в базисном, но это произошло вследствие увеличения посевной площади на 300 га (4500-4200), при снижении средней урожайности на 0,7 ц/га (22,4-23,1).
Пример решения задачи 4
По данным выборочного обследования получено следующее распределение работников организации по размеру заработной платы:
| Группы работников по размеру среднемесячной заработной платы, руб. | 12 000- 13 000 | 13 000- 14 000 | 14 000- 15 000 | 15 000- 16 000 | 16 000- 17 000 |
| Число работников |
Определите:
1) среднюю заработную плату;
2) коэффициент вариации;
3) моду и медиану.
Решение
1. Условие задания представлено интервальным вариационным рядом с равными интервалами. Поэтому для вычисления показателей сначала следует определить величину осредняемого признака (х) как середину каждого интервала и получить дискретный ряд распределения.
| Месячная заработная плата, руб. | 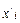 | 12 500 | 13 500 | 14 500 | 15 500 | 16 500 | Итого |
| Число работников | mi |
Далее производим расчет по средней арифметической взвешенной:
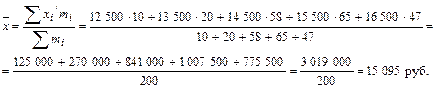
2.Коэффициент вариации характеризует меру колеблемости отдельных вариантов признака (х) вокруг средней величины. Он представляет собой процентное соотношение среднего квадратического отклонения (σ) и средней арифметической 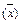 , т.е.
, т.е.
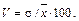
Для расчета среднего квадратического отклонения предварительно вычислим дисперсию (σ2)по формуле
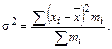
Расчет можно выполнить с помощью вспомогательной таблицы:
| x | m | х - 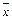 | (х - 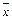 )2 )2 | (х - 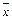 )2m )2m |
| 12 500 | 12 500-15 095 | 6 734 025 | 67 340 250 | |
| 13 500 | 13 500-15 095 | 2 544 025 | 50 880 500 | |
| 14 500 | 14 500-15 095 | 354 025 | 20 533 450 | |
| 15 500 | 15 500-15 095 | 164 025 | 10 661 625 | |
| 16 500 | 16 500-15 095 | 1 974 025 | 92 779 175 | |
| Итого | - | - | 242 195 000 |
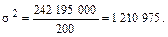
Среднее квадратическое отклонение - это корень квадратный из дисперсии:
σ = ±√ σ2 = ± 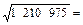 ±1100,443 руб.
±1100,443 руб.
Коэффициент вариации
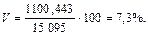
Если значение коэффициента вариации не превышает 33,3%, то совокупность считается однородной, а средняя величина может быть признана типичной для данного распределения. В нашем примере средняя величина типична.
3. Мода (доминанта) - это наиболее часто встречающееся значение признака x; в интервальном ряду модальным будет тот интервал, который имеет наибольшую частоту (частость).
В данном задании наибольшую частоту (65) имеет интервал 15 000 - 16 000 руб., следовательно, мода и будет находиться в этом интервале.
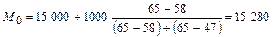 руб.
руб.
Следовательно, наибольшее число работников имели заработную плату в размере 15 280 руб.
Медиана - значение признака у той единицы ранжированного ряда, которая находится в его середине. Сначала определим порядковый номер этой единицы. Для этого добавим к сумме всех частот ряда 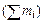 единицу и результат разделим пополам, т.е.
единицу и результат разделим пополам, т.е.
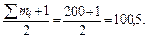
Медианным значением зарплаты будет то, которое составит полусумму зарплат 100-го и 101-го работников. Они попадают в четвертый интервал (10+20+58+65=153) по сумме накопленных частот, т.е. от 15 000 до 16 000 руб.
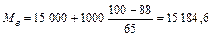 руб.
руб.
Следовательно, половина работников имеют заработную плату не более 15 184,6 руб., а другая половина - не менее 15 184,6 руб.
Задачи 5-6 предполагают исследование динамики показателей, т.е. интенсивности изменения явлений во времени, которые осуществляются с помощью следующих индикаторов: абсолютных приростов, темпов роста, темпов прироста, абсолютного значения одного процента прироста, а также средних обобщающих показателей.
В зависимости от задачи исследования показатели могут быть исчислены с переменной базой сравнения (цепные) и с постоянной базой сравнения (базисные).
1. Абсолютный прирост - это разность между сравниваемым уровнем и предыдущим или базисным:
· цепной абсолютный прирост: 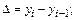
· базисный абсолютный прирост: 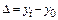 .
.
Сумма цепных абсолютных приростов равна базисному абсолютному приросту за соответствующий период времени.
2. Темп роста - относительный показатель, характеризующий интенсивность развития явления; он равен отношению изучаемого уровня к предыдущему или базисному и выражается в коэффициентах или процентах:
· цепной темп роста: 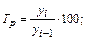
· базисный темп роста: 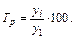
Произведение соответствующих цепных темпов роста, исчисленных в коэффициентах, равно базисному.
3. Темп прироста определяют двумя способами:
а) как отношение абсолютного прироста к предыдущему уровню (цепной) или базисному уровню (базисный):
цепной темп прироста: 
базисный темп прироста: 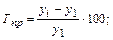
б) как разность между темпом роста и 100%:
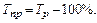
4. Абсолютное значение одного процента прироста определяется как отношение цепного абсолютного прироста к цепному темпу прироста (%) или для каждого последующего уровня - как 0,01 предыдущего уровня ряда динамики:
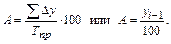
5. Средний абсолютный прирост вычисляется по средней арифметической простой, т.е. делением суммы цепных абсолютных приростов на их число:
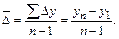
Средний темп роста находят по формуле средней геометрической:
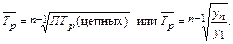
Средний темп прироста находят путем вычитания из среднего темпа роста 100%:
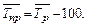
Методы расчета среднего уровня ряда динамики зависят от его вида и полноты информации:
1) в интервальных рядах с равными интервалами времени средний уровень определяется по формуле средней арифметической простой;
2) в интервальных рядах с неравными интервалами времени - по формуле средней арифметической взвешенной (по величине интервалов);
3) в моментных рядах с исчерпывающими данными об изменении моментного показателя расчет производится по средней арифметической из уровней ряда, сохранявшихся неизменными в течение определенных промежутков времени, взвешенной по величине соответствующих промежутков;
4) в моментных рядах динамики с равноотстоящими уровнями применяется формула средней хронологической простой;
5) в моментных рядах динамики с неравными промежутками времени между уровнями - средняя хронологическая взвешенная.
Пример решения задачи 5
Имеются следующие данные о производстве продукции предприятия за 6 лет (в сопоставимых ценах, млн. руб.):
| 8,0 | 8,4 | 8,9 | 9,5 | 10,1 | 10,8 |
Рассчитайте:
1) цепные и базисные абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста;
2) среднегодовые значения абсолютного прироста, темпа роста и прироста;
3) средний уровень ряда динамики.
Решение
Абсолютные приросты
| Год | Базисные | Цепные |
| 8,0 - 8,0 = 0 | - | |
| 8,4 - 8,0 = 0,4 млн. руб. | 8,4 - 8,0 = 0,4 млн. руб. | |
| 8,9 - 8,0 = 0,9 млн. руб. | 8,9 - 8,4 = 0,5 млн. руб. | |
| и т.д. |
Сумма цепных абсолютных приростов равна базисному абсолютному приросту для любого года. Так, для 2008 г.:
0,4 + 0,5 + 0,6 + 0,6 + 0,7 = 2,8.
Коэффициенты (темпы) роста
| Год | Базисные | Цепные |
| 8,0 / 8,0 = 1, или 100% | - | |
| 8,4 / 8,0 = 1,050, или 105,0% | 8,4 / 8,0 = 1,050, или 105,0% | |
| 8,9 / 8,0 = 1,112, или 111,2% | 8,9 / 8,4 = 1,059, или 105,9% | |
| и т.д. |
Произведение цепных коэффициентов роста равно базисному коэффициенту роста. Для 2008 г.:
1,050 · 1,059 · 1,067 · 1,063 · 1,069 = 1,350.
