Дисперсия альтернативного признака

Понятие вариации

Средняя дает обобщающую характеристику всей совокупности изучаемого явления.

Вариацией признака называется различие индивидуальных значений признака внутри изучаемой совокупности.

Средняя величина является абстрактной, обобщающей характеристикой признака изучаемой совокупности, но она не показывает строение совокупности.

Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от неё.

Если отдельные значения признака близки к средней арифметической, то в этом случае средняя хорошо представляет всю совокупность. И наоборот.

Колеблемость отдельных значений характеризуют показатели вариации.

Термин «вариация» произошел от латинского variatio – изменение, колеблемость, различие. Однако не всякие различия принято называть вариацией.

Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака в абсолютных и относительных величинах. Абсолютная – R, L, σ, σ ².

Показатели вариации

1 совокупность	2 совокупность
n=5 80, 100, 120, 200, 300	n=8 145, 150, 155, 160, 160, 162, 168, 180

x=160 x=160

145 x 180

80 100 120 x 200 300

Поэтому в этом случае возникает необходимость определить вариацию признака, т.е. соотношение отдельных значений ряда относительно друг друга.

Вывод: чем больше вариация, тем дальше в среднем отдельные значения лежат друг от друга.

Показатели вариации

1. Размах вариации, представляет собой разность между максимальным и минимальным значением признака.

R = X_max - X_min

R₁ = 300-80=220 R₂=180-145=35

Практика: для однородной совокупности, для контроля качества продукции.

2. Показатели, учитывающие отклонения всех вариантов от средней арифметической.

а) Среднее линейное отклонение

б) Среднее квадратическое отклонение

Среднее линейное отклонениепредставляет собой среднее арифметическое из абсолютных значений отклонений отдельных вариантов от средней.

для не сгруппированных:

;

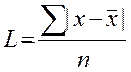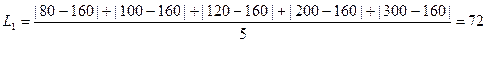
для сгруппированных:

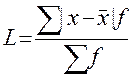
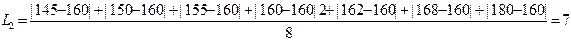
Практика: с его помощью анализируется:

1. Состав работающих

2. Ритмичность производства

3. Равномерность поставок материалов

Недостаток: этот показатель усложняет расчеты вероятного типа, затрудняет применение методов математической статистики

Среднее квадратическое отклонение (стандартное) – это

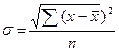для не сгруппированных данных

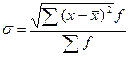для сгруппированных данных

Для умеренно асимметричных распределений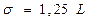

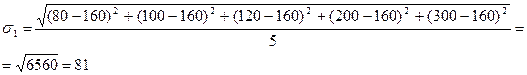
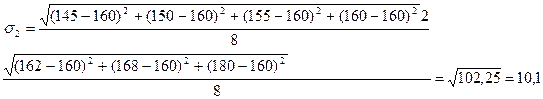
Среднее квадратическое отклонение, как и среднее линейное отклонение – это абсолютный показатель, выражается в тех же единицах, что и среднее арифметическое.

Показатели среднего квадратического или среднего линейного отклонений для двух совокупностей оказываются несопоставимыми, если сами 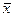признака у этих совокупностей неодинаковы. Несопоставляются эти показатели и для разных признаков одной совокупности. Т.е. когда средние в обеих совокупностях выражены в одних и тех же единицах измерения и одинаковы, сопоставление возможно и отразит различия в вариации признака.

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше σ, тем лучше среднее арифметическое отражает собой всю представляемую совокупность.

3.Дисперсия используется для измерения колеблемости признака. Этот показатель более объективно отражает меру вариации

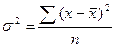для не сгруппированных

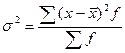для сгруппированных

Отличительной особенностью данного показатели является то, что при возведении в квадрат удельный вес малых отклонений падает, а больших увеличивается в общей сумме отклонений.

Это тоже абсолютный показатель

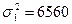
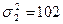
Дисперсия обладает рядом свойств, некоторые из них позволяют упростить её вычисление:

1. Дисперсия постоянной величины равна 0

2. Если все варианты значений признака (x) ↓ на одно и то же число, то дисперсия не уменьшается

3. Если все варианты ↓ в одно и то же число раз (K раз), то дисперсия ↓ в К² раз

x	f	x'

x ↑ в 100 раз

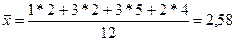
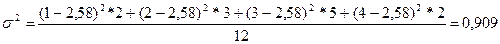
Дисперсия σ равна 0,909*10000=9090

Выше был рассмотрен расчет показателей вариации для количественных признаков, но может ставиться задача оценки вариации качественных признаков. Например, при изучении качества изготовленной продукции можно разделить на годную и бракованную.

В таком случае речь идет об альтернативных признаках.

Дисперсия альтернативного признака

Альтернативными признаками называются такие, которыми одни единицы совокупности обладают, а другие нет. Например, наличие производственного стажа у абитуриентов, ученая степень у преподавателей ВУЗов и т.д. Наличие признака у единиц совокупности условно обозначаем через 1, а отсутствие – 0. х₁=1, х₂=0. Долю единиц, обладающих признаком (в общей совокупности) обозначаем через р, а долю единиц, не обладающих – через q. Т.е. p+q=1, q=1-p.

Рассчитаем среднее значение альтернативного признака

; ;

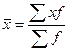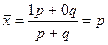Т.е. среднее значение альтернативного признака равно доли единиц, обладающих данными признаками, на долю единиц, не обладающих данными признаками.

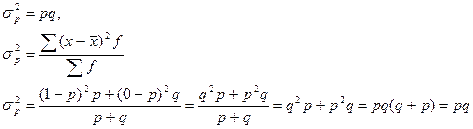
Среднее квадратическое отклонение равно Б_p=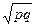

Пример.

Проверяется качество: 1000 готовых изделий, 20 бракованных.

1-20

0-980

Находим долю брака: (20/1000)*100%=0,02%

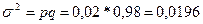
Дисперсия обладает рядом свойств, которые позволяют упростить расчет.

1. Если из всех значений вариант отнять какое-то постоянное число А, то среднее квадратическое отклонение от этого не изменится.

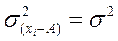
2. Если все значения вариант разделить на какое-то постоянное число А, то среднее квадратическое отклонение уменьшится от этого в А² раз, а среднее квадратическое отклонение в А раз.

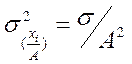
3. Если исчислить среднее квадратическое отклонение от 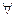величины А, которая в той или иной степени отличается от средней арифметической 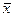, то он всегда будет больше среднего квадратического отклонения σ², исчисленного от среднего арифметического.

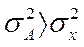
При этом больше на вполне определенную величину – на квадрат разности между средней и этой условно взятой величиной, т.е. на :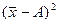

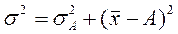или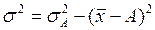

Дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от 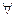других величин.

В этом случае, когда А=0, и, следовательно, не вычисляем отклонения.

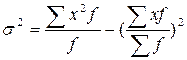
или

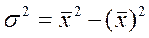
средний квадрат значений признака m₂

квадрат среднего значения признака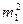

Этой формулой удобно пользоваться для наибольших значений вариантов.

Средняя величина отражает тенденцию развития, т.е. действие главных причин (факторов).

σ измеряет силу воздействия прочих факторов.