Статистические данные для самостоятельного решения задач

СТАТИСТИКА

Методические указания по выполнению

Практических и лабораторных работ

Часть 3

Издание стереотипное

Великий Новгород

ББК 60.6	Печатается по решению
С78	РИС НовГУ

Рецензент

кандидат физико-математических наук Н.В. Манова

С78	Статистика: Методические указания по выполнению практических и лабораторных работ. Часть 3 / Сост.: Л.И. Бернасовская, Н.И. Гришакина, Г.В. Лебедева, О.Д. Притула, Г.В. Фетисова; НовГУ им. Ярослава Мудрого. - Великий Новгород, 2011. – 37 с.

Методические указания содержат поэтапную характеристику выполнения практических и лабораторных работ вручную и с использованием ППП, примеры решения, задачи для самостоятельного решения студентов экономических специальностей.

Учебно-методическое пособие предназначено для студентов дневной и заочной форм обучения.

ББК 60.6

© Новгородский государственный

университет, 2011

© Л.И. Бернасовская, Н.И. Гришакина, Г.В. Лебедева, О.Д. Притула, Г.В. Фетисова

составление, 2011

СОДЕРЖАНИЕ

Введение…………………………………………………………………………………………………..4

Практическая работа 5. Дисперсионный анализ……………………………………………………….5

Лабораторная работа 7. Однофакторный дисперсионный анализ в ППП “Microstat”

и в ППП Statistica”..……………………….….…….…………………………….……………………..21

Лабораторная работа 8. Дисперсионный анализ в MS EXCEL……………….……………………...26

Список литературы……………………………………………………………………………………...28

Приложения

ВВЕДЕНИЕ

Методические указания по выполнению практических и лабораторных работ по статистике содержат требования по их выполнению, порядок расчетов вручную и с использованием ППП Microstat, MS Excel, Statistica.

В части III методических указаний представлен дисперсионный анализ, который широко используется для планирования эксперимента и статистической обработки его данных. Он был разработан и введен в практику английским ученым Р.А. Фишером. Если в недалеком прошлом считали, что роль математики состоит лишь в анализе данных, то работы Р.А. Фишера коренным образом изменили эту точку зрения, и в настоящее время статистическое планирование опыта в соответствии с требованиями дисперсионного анализа и математическая интерпретация результатов – непременное условие успешного получения ответов на вопросы, интересующие экспериментатора. Статистически обоснованный план эксперимента определяет метод экономического анализа результатов. Поэтому современный эксперимент нельзя правильно спланировать, не зная основ дисперсионного анализа.

Более доступными и наглядными методы анализа данных сделали современные пакеты прикладных программ. Они являются быстродействующим средством для проведения дисперсионного анализа данных пользователем, который должен обладать определенными знаниями статистических методов, знать их свойства и уметь анализировать и использовать полученные результаты.

Цель данного пособия – ознакомление широкого круга исследователей с одним из важнейших статистических методов анализа, и применение его на практике.

ПРАКТИЧЕСКАЯ РАБОТА 5

ДИСПЕРСИОННЫЙ АНАЛИЗ

Цель работы: получение практических навыков статистической обработки многовариантных, многофакторных экспериментов, когда анализируется влияние одного, двух, трех и большего числа факторов на изменение величины какого-либо признака.

Порядок выполнения работы:

1. Установление основных источников варьирования и определение объемов вариации по источникам образования.

2. Определение числа степеней свободы вариации.

3. Вычисление дисперсий и анализ соотношений между ними.

4. Интерпретация полученных результатов анализа.

Дисперсионный анализ быстро вошел в употребление благодаря следующим основным преимуществам:

1. В дисперсионном анализе используется обобщенная ошибка средних, которая опирается на большое число наблюдений.

2. Этим методом можно обрабатывать данные простых и сложных, однолетних и многолетних, однофакторных и многофакторных опытов.

3. Позволяет компактно в виде существенных разностей представить итоги статистической обработки.

При дисперсионном анализе проводят расчет дисперсий:

- общей (дисперсия комплекса);

- межгрупповой (факторная);

- внутригрупповой (остаточная).

Общая дисперсия ( 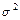) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:

.

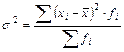Межгрупповая дисперсия ( 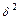) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.

,

где - групповые средние,

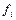- численность единиц в группе.

Внутригрупповая дисперсия ( 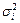) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки:

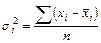- для несгруппированных данных;

- для сгруппированных данных.

Средняя из внутригрупповых дисперсий определяется следующим образом:

.

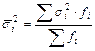Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

.

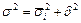Данное соотношение называют правилом сложения дисперсий.

Правило сложения дисперсий широко применяется при исчислении показателей тесноты связи.

В статистическом анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии. Он носит название эмпирического коэффициента детерминации( ):

.

Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака, обусловленную вариацией группировочного признака.

Эмпирическое корреляционное отношение ( 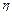) характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака:

.

Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Если , то группировочный признак не оказывает влияния на результативный. Если 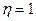, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю.

Дисперсионный анализ – метод оценки существенности различий нескольких средних. Его применяют при статистической обработке многовариантных, многофакторных опытов.

Критерий, используемый для оценки различий между выборочными средними, назван в честь Р.Фишера критерием F – распределения. Критерий F представляет собой отношение двух дисперсий:

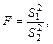
где и 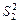- средние квадраты (дисперсии), рассчитанные по выборочным данным с учетом числа степеней свободы вариации[1].

Теоретическое значение F показывает случайную величину отношения двух дисперсий при данном уровне вероятности суждения и соответствующем числе степеней свободы анализируемых дисперсий. Критерий F связывают с вероятностью. Наиболее часто применяют уровни вероятности суждения – 0,95 и 0,99 (5 и 1%-ный уровни). Это означат, что только в пяти (в одном) случаях из 100 значение F может достигать табличного уровня или быть больше него для отношения дисперсий двух выборок, сделанных из одной и той же генеральной совокупности.

Табличное значение F используется как критерий для оценки фактических отношений дисперсий, рассчитанных по выборочным данным. Если F_факт > F _табл, мало вероятно, что такое отношение случайное. А, значит, и различия в вариации нельзя отнести только за счет случайного колебания их уровня, и разница между средними существенна. В случае, когда F_факт ≤ F _табл, при данном уровне вероятности суждения и соответствующем числе степеней свободы это означает, что различия между сравниваемыми дисперсиями находятся в пределах возможных случайных колебаний.

Порядок проведения дисперсионного анализа идентичен при простых моделях, когда группировочный признак один, и при сложных моделях, когда группировочных признаков два или больше. Но с увеличением числа группировочных признаков более сложен процесс расчленения вариации по источникам образования.

При группировке по одному признаку общий объем вариации можно разложить на вариацию, связанную с действием группировочного признака, и вариацию внутригрупповую (остаточную):

.

Исходные данные для проведения однофакторного дисперсионного анализа могут быть представлены в виде статистической таблицы (таблица 1).

Таблица 1 - Исходные данные.

Вариант	Исходные данные, y
	y11	y12	…	y1n
	y21	y22	…	y2n
…	…	…	…	…
i	yi1	yi2	…	yin

При группировке по одному признаку группы могут быть равными и неравными, сформированы в случайном порядке, когда наблюдения одной группы не связаны с наблюдением другой группы, или неслучайном, когда наблюдения одной группы связаны с наблюдениями другой группы.

В опытах, где формируются группы соответственно числу повторностей по каждому варианту, схема дисперсионного анализа предусматривает исключение из общего объема вариации тех колебаний, которые обусловлены влиянием фактора, различиями в повторах и индивидуальными различиями внутри каждой группы.

Таким образом, общая сумма квадратов подразделяется на сумму квадратов отклонений вариантов опыта (групповая), сумму квадратов отклонений повторений и остаточную сумму квадратов:

.

Данные для обработки такого вида комплекса можно представить в виде статистической таблицы (таблица 2):

Таблица 2 - Расположение данных в таблице для проведения дисперсионного анализа однофакторного сопряженного статистического комплекса.

Вариант	Повторения
			…	n
	y11	y12	y13	…	y1n
	y21	y22	y23	…	y2n
…	…	…	…	…	…
i	yi1	yi2	yi3	…	yin

При группировке данных по двум признакам общая сумма квадратов отклонений будет иметь уже две групповые суммы квадратов и сумму квадратов отклонений взаимодействия факторов и остаточную:

.

Исходные данные для проведения двухфакторного дисперсионного анализа с повторениями представлены в виде таблицы (таблица 3):

Таблица 3 - Расположение данных в таблице для двухфакторного дисперсионного анализа с повторениями.

Вариант	Аm
В1	В2	…	Вn
	y11	y12	…	y1n
	y21	y22	…	y2n
…	…	…	…	…
i	yi1	yi2	…	yin

Если формирование групп будет неслучайным, разложение сумм квадратов усложнится. В итоге при группировке по двум признакам и неслучайном распределении повторностей по группам дисперсионный анализ проводится по следующей схеме:

.

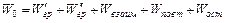После того, как определены суммы квадратов, необходимо установить степени свободы вариации, соответствующие каждой сумме квадратов.

При группировке данных по одному признаку и случайному распределению повторностей в группах общее число степеней свободы составит 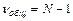, для групповой вариации 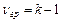(количество средних k минус 1), для остаточной вариации 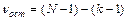(общее число степеней свободы минус число степеней свободы для групповой вариации). Определение числа степеней свободы при группировке по одному (двум) признакам и неслучайном распределении повторностей далее рассмотрено на конкретных примерах.

После определения числа степеней свободы и суммы квадратов отклонений рассчитываются групповая и остаточная дисперсии:

Дисперсия групповая ( ) характеризует в среднем вариацию, обусловленную влиянием группировочного признака и определяется так:

.

Дисперсия остаточная ( 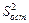) измеряет вариацию, обусловленную случайными причинами, которые не учитывались при распределении данных наблюдений на группы:

.

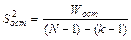Если групповая дисперсия значительно больше остаточной, то фактор оказывает существенное влияние на величину признака. Фактическое отношение групповой дисперсии к остаточной ( 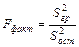) сравнивают с табличным значением F.

Отношение дисперсий групповой и остаточной позволяет сделать с определенной вероятностью вывод о том, достоверны ли различия в средних. Если есть необходимость сделать заключение об отдельных парах средних, этот вывод недостаточен.

Поэтому результаты дисперсионного анализа дополняются оценкой достоверности разности между двумя средними.

Для этого рассчитывается средняя ошибка выборочных средних на основе остаточной дисперсии:

.

Средняя ошибка разности двух средних - корень квадратный из суммы квадратов средних ошибок сравниваемых средних, но так как m² одинакова для всех средних,

.

Принимая доверительный уровень вероятности по таблицам t Стьюдента, определяют критическую величину t.

На основе средней ошибки разности двух средних 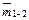и t_табл вычисляют возможную предельную ошибку этой разности:

.

Предельная ошибка сопоставляется с разностью двух сравниваемых средних:

.

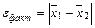Если разница между средними больше по абсолютной величине возможной предельной ошибки, то делается вывод о существенности разности средних. Если же 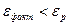, то разница между средними лежит в границах возможных случайных колебаний, т.е. она недостоверна.

Величину принято называть наименьшей существенной разностью.

Рассмотрим дисперсионный анализ на конкретных примерах.

Пример 1.

Имеются данные о заработной плате 20 работников фирмы:

Таблица 4 - Данные о заработной плате работников фирмы.

№п/п
З/пл, тыс. руб.	1,3	1,7	2,3	2,7	3,0	3,2	3,4	3,5	3,6	3,7	3,9	4,2	4,4	4,5	4,7	4,8	5,0	5,2	5,7	5,8

Используя правило сложения дисперсий, определить степень влияния уровня образования работников на заработную плату, если работники со средним специальным образованием имеют заработную плату до 3,5 тыс. руб., с высшим – более 3,5 тыс. руб.

Для определения степени влияния образования работников на их заработную плату, определяем группировочный признак и строим таблицу. Результативным признаком является заработная плата, факторным – образование работников.

Таблица 5 - Распределение заработной платы работников в зависимости от уровня образования.

Среднее специальное	Высшее
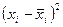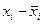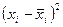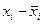№ п/п	з/пл, тыс. руб. xi			№ п/п	з/пл, тыс. руб. xi
	1,3	-1,3	1,69		3,6	-1,0	1,00
	1,7	-0,9	0,81		3,7	-0,9	0,81
	2,3	-0,3	0,09		3,9	-0,7	0,49
	2,7	0,1	0,01		4,2	-0,4	0,16
	3,0	0,4	0,16		4,4	-0,2	0,04
	3,2	0,6	0,36		4,5	-0,1	0,01
	3,4	0,8	0,64		4,7	0,1	0,01
	3,5	0,9	0,81		4,8	0,2	0,04
					5,0	0,4	0,16
					5,2	0,6	0,36
					5,7	1,1	1,21
					5,8	1,2	1,44
Итого:	21,1		4,57	Итого:	55,5		5,73

Внутригрупповые дисперсии определим по формуле:

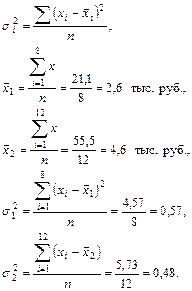
Внутригрупповые дисперсии показывают вариацию заработной платы по группам, вызванные всеми возможными факторами (стаж работы, квалификация, должность, производительность труда и др.), кроме образования работников.

Среднюю из внутригрупповых дисперсий определим по формуле:

.

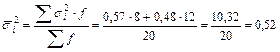Межгрупповая дисперсия исчисляется по формуле:

.

Определим общую среднюю по формуле средней арифметической простой:

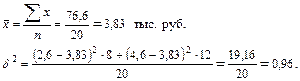
Межгрупповая дисперсия показывает вариацию заработной платы, обусловленную влиянием образования работников.

Общую дисперсию определяем на основании правила сложения дисперсий:

Определим долю межгрупповой дисперсии в общей с помощью эмпирического коэффициента детерминации:

На 64,9% вариация заработной платы обусловлена влиянием уровня образования работников и на 35,1% (100-64,9) влиянием прочих факторов, не учтенных в группировке.

Эмпирическое корреляционное отношение:

.

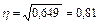Эмпирическое корреляционное отношение показывает тесноту связи между результативным и факторным признаком. Оно равно 0,81, следовательно, связь между заработной платой и уровнем образования работников - тесная.

Пример 2. Дисперсионный анализ при группировке данных по одному признаку (неслучайное распределение наблюдений в группах).

Правление фирмы решает изучить результаты продвижения на книжный рынок научной литературы, надеясь извлечь из них информацию, которой можно было бы воспользоваться при организации и проведении компании по распространению новых изданий.

С этой целью была выделена контрольная группа продавцов, не имеющих опыта работы. Вторая группа имела стаж работы 1-3 года. Третью группу составляли работники со стажем более 3-х лет.

Чтобы обеспечить по всем трем вариантам выровненные условия, были сформированы пять групп, приблизительно равноценных по показателям. Каждая группа включала 3 человека. Результаты работы приведены в таблице 6.

Таблица 6 - Количество проданной научной литературы, шт. (в среднем за месяц).

Варианты опыта	Повторности	Суммы	Средние
I группа (контр.)
II группа
III группа
Суммы
Средние							Х

Проведение исследования таково, что наблюдения в каждом варианте связаны общностью условий, т.е. распределение повторностей в группах неслучайное. Порядок построения опыта делает необходимым исключение из общей суммы квадратов отклонений вариации, определяемой стажем, повторностями и остаточной вариацией:

.

Требуется статистически оценить результаты исследований в целом и попарно сравнить средние по стажу. Уровень вероятности суждения 0,05.

Решение.

1. Выдвинем гипотезу, что различия в средних стажа работы случайны, и рассчитаем показатели, необходимые для заключения выдвинутой гипотезы.

2. Данные таблицы 6 для удобства вычислений целесообразно уменьшить на постоянную величину (А), близкую к значению средней. Результаты занесем в таблицу 7.

Таблица 7 - Отклонения от условного начала у = х – А, А = 350

Вариант опыта	Повторности	Сумма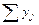
I группа (контр.)	-3	-19	-15	-17	-23	-77
II группа				-5	-1
III группа
Суммы	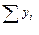			-15	-12	120 =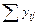

Проверим правильность вычислений:

,

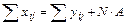где N = 15 – общее число наблюдений (N = k · n = 3 · 5 = 15),

k - число вариантов,

n – число наблюдений в каждом варианте.

.

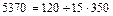3. Все отклонения от условного начала, суммы по столбцам и строкам возведем в квадрат (табл. 8).

Таблица 8 - Таблица квадратов.

Вариант опыта	Повторности	Сумма квадратов	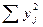Квадрат суммы
I группа (контр.)
II группа
III группа
Сумма квадратов	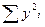					7816	27998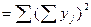
Квадрат сумм						7964	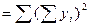14400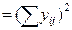

Рассчитаем суммы квадратов отклонений по данным таблицы 8.

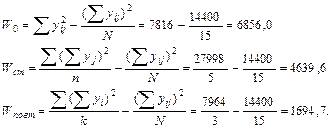
Затем определим остаточную сумму квадратов как разность:

.

4. Далее необходимо определить число степеней свободы вариации для каждой суммы квадратов отклонений:

5. Для того, чтобы определить дисперсии, следует разделить суммы квадратов отклонений на соответствующее число степеней свободы. Результаты расчетов занесем в следующую таблицу.

Таблица 9 - Анализ дисперсий.

Источник вариации	Сумма квадратов отклонений	Степень свободы вариации	Дисперсия	Отношение дисперсии
Fфакт	Fтабл
Стаж	4639,6		2319,8	35,6	4,46
Повторности	1694,7		423,7	6,5	3,84
Остаточная	521,7		65,2	1,0
Общая	6856,0		X1

6. Вариацию внутри групп (случайную вариацию) определяет , равная 65,2, ее и принимают за базу сравнения.

Определим фактическое отношение дисперсий:

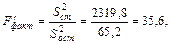
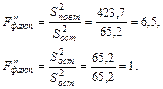
Проведенные расчеты показывают, что дисперсии стажа и повторностей значительно превышают остаточную дисперсию.

7. Воспользуемся приложением А и определим F_табл при уровне вероятности суждения 5% (0,05). Значение F_табл находим на пересечении столбца и строки (соответствующих степеням свободы). Например:

Таким образом, для оценки отношения F_табл = 4,46, а для оценки отношения .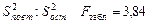

Фактические отношения дисперсий (35,6 и 6,5) значительно превышают пределы возможных случайных колебаний (4,46 и 3,84), поэтому следует отказаться от гипотезы, что различия в средних стажа работы несущественны.

8. Проведенный дисперсионный анализ выявил существенность различий между средними в целом. Приступим к оценке существенности разностей между каждой парой средних. Для этого необходимо вычислить среднюю ошибку разности средних:

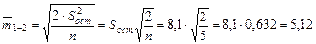шт. за месяц;

шт. за месяц.

9. Обратимся к приложению Б Значение критерия t-Стьюдента.

При вероятности 0,05 и 8 степенях свободы вариации значение нормированного t равно 2,3060≈2,31. Тогда предельная ошибка составит:

штук.

Мы определили величину возможных случайных колебаний при заданном уровне вероятности. Сопоставим разность объема проданной литературы, соответствующей стажу работы и размер предельной ошибки. Если разность превышает предельную ошибку, то ее принято считать существенной.

Возможны следующие сопоставления:

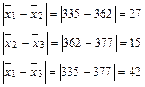
Полученные результаты превышают по абсолютной величине предельную ошибку. Это позволяет нам заключить, что они существенны.

СТАТИСТИЧЕСКИЕ ДАННЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ЗАДАЧ

ЗАДАНИЕ 1

Вариант 1.

Известны данные о прибыли 24 предприятий, млн. руб.:

26,0	30,0	27,3	38,1	30,0	28,0
31,5	40,0	30,0	21,5	33,0	35,1
29,1	20,0	33,0	31,5	30,0	29,1
25,1	34,1	29,1	30,0	33,5	22,0

Определить степень влияния опыта работы предприятий на величину прибыли, если известно, что первые 10 предприятий имели опыт работы менее 2-х лет, а остальные 14 – более 2-х лет.

Вариант 2.

Известны данные об объеме вложений в ценные бумаги 24 банков России, млрд. руб.:

2,7	4,6	4,0	3,7	4,1	3,2
4,8	1,9	4,8	4,0	4,9	4,3
2,8	4,3	3,2	2,4	4,0	3,7
4,0	3,4	5,6	3,4	4,6	2,5

Определить степень влияния прибыли на объемы вложений в ценные бумаги, если первые 15 банков имели прибыль до 50 млрд. руб., а остальные 9 – свыше 50 млрд. руб.

Вариант 3.

Имеются данные о чистых активах 24 банков России, млрд. руб.:

39,9	49,5	44,2	54,2	42,9	39,6
43,0	35,1	42,9	39,6	48,6	41,7
48,1	41,0	49,0	43,0	39,1	51,8
39,6	45,0	39,0	39,9	49,0	39,6

Определить степень влияния прибыли на величину чистых активов, если известно, что первые 10 банков имели прибыль до 111 млрд. руб., а остальные 14 – свыше 111 млрд. руб.

Вариант 4.

Имеются данные о кредитных вложениях 24 банков России, млрд. руб.:

19,8	21,4	19,9	21,1	19,9	24,0
21,1	22,0	18,0	21,5	26,0	18,9
24,2	18,2	24,6	19,9	18,5	23,5
19,5	25,0	20,0	23,0	21,5	19,8

Определить степень влияния ставки кредитов на величину кредитных вложений банков, если известно, что кредитные вложения до 20 млрд. руб. имели банки с минимальной ставкой кредита, а свыше 20 млрд. руб. – с максимальной ставкой кредита.

Вариант 5.

Известны данные о прибыли 24 предприятий региона, млн. руб.:

15,2	23,9	17,7	16,9	13,2	19,1
26,2	17,6	22,7	20,0	19,1	15,1
14,3	23,1	11,6	17,6	22,5	26,2
19,1	16,9	23,1	24,1	17,7	14,7

Определить степень влияния формы собственности предприятия на прибыль, если известно, что величина прибыли до 17 млн. руб. принадлежит АО, а свыше 17 млн. руб. – кооперативам.

Вариант 6.

Известны данные о заработной плате 24 работников фирмы, тыс. руб.:

3,3	2,4	2,6	3,0	1,8	4,2
2,2	2,9	4,2	2,8	3,5	2,5
2,6	2,8	1,5	2,6	2,4	3,5
2,3	2,5	3,0	2,9	3,3	2,6

Определить степень влияния формы оплаты труда на заработную плату работников, если работники со сдельной оплатой труда имели заработную плату до 3 тыс. руб., с повременной – свыше 3 тыс. руб.

ЗАДАНИЕ 2

Необходимо проанализировать производительность труда рабочих одного из цехов НПО “Виктория”. С этой целью была образована контрольная группа рабочих, имеющих стаж работы до 1 года, во вторую группу вошли рабочие со стажем от 1 до 3 лет и в третью группу объединили рабочих с большим стажем. Для чистоты эксперимента были сформированы пять групп, приблизительно равноценных по показателям. Результаты приведены в таблице 10.

Таблица 10 - Производительность труда рабочих цеха НПО “Виктория”, деталей за смену, штук.

Номер варианта	Вариант опыта	Повторность
	I группа (контр.)
II группа
III группа
	I группа
II группа
III группа
	I группа
II группа
III группа
	I группа
II группа
III группа
	I группа
II группа
III группа
	I группа
II группа
III группа

Пример 3. Дисперсионный анализ при группировке данных по двум признакам (неслучайное распределение повторностей в группе)

Проанализировав результаты по реализации литературы (пример 2), правление фирмы пришло к выводу о необходимости продолжения эксперимента. Цель опыта состояла в том, чтобы уловить эффект взаимодействия между стажем работы и полом сотрудников.

Участники эксперимента предварительно были разделены на 2 части (блока). Одну часть (блок) составляли одни мужчины, другую – женщины. Каждый блок включал в себя группы по стажу работы: контроль – проработавшие в этой сфере менее года, 1 гр. – со стажем 1 год, 2 гр. – соответственно – 2 года и 3 гр. – 3 и более лет. Опыт проведен в трехкратной повторности. Следовательно, распределение в каждом варианте неслучайное.

Результаты эксперимента приведены в таблице 11.

Таблица 11 - Количество проданной научной литературы, шт. (в среднем за месяц)

Пол	Вариант опыта	Повторности	Сумма	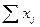Средние
Мужской	Контроль
Стаж:
1 год
2 года
3 года
Суммы					Х
Средние по группе				Х
Женский	Контроль
Стаж:
1 год
2 года
3 года
Суммы					Х
Средние по группе				Х
	Суммы	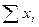			4866=	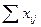Х
Средние по повторностям				Х
Средние по подгруппам:
Контроль				Х
Стаж:
1 год				Х
2 года				Х
3 года				Х

Требуется оценить достоверность различий между средними по вариантам опыта, используя дисперсионный метод анализа.

Решение.

1. Выдвигаем гипотезу о том, что факторы не оказывают влияния на реализацию литературы. Заключение по гипотезе сделаем с вероятностью 0,05. Количество реализуемой литературы варьировало в зависимости от пола, стажа работы, от сочетания этих факторов, от различий в составе групп, а так же не исключается случайное варьирование. Исходя из перечисленного, общую сумму квадратов отклонений следует представить как сумму:

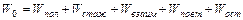
Разложение проведем в два этапа.

На первом этапе разложим:

;

а на втором -

.

Определим число наблюдений. Анализируются 2 части (блока), т.е. k = 2. Второй фактор – стаж работы имеет 4 группы, l = 4. Каждый вариант представлен 3 повторами, т.е. n = 3. Общее число наблюдений N = k · l · n = 2 · 4 · 3 = 24.

2. Для упрощения вычислений выразим результаты эксперимента в отклонениях от постоянной величины А. За А принимается величина, близкая к общей средней (А = 200).

Результаты занесем в таблицу 12.

Таблица 12 - Таблица отклонений.

Пол	Вариант опыта	Повторности	Сумма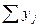
Мужской	Контроль	-67	-46	-66	-179
Стаж:
1 год	-38	-29	-21	-88
2 года
3 года
Женский	Контроль		-14	-10	-13
Стаж:
1 год
2 года
3 года
Сумма				66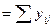

3. Проверим правильность проведенных преобразований:

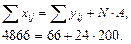
Определим общую сумму квадратов, суммы квадратов всех вариантов опыта, повторностей:

.

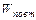Возводя в квадрат данные табл. 12, получим значения для определения и . Результаты вычислений поместим в таблицу 13:

Таблица 13 - Таблица квадратов отклонений.

Пол	Вариант опыта	Повторности	Сумма квадратов	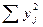Квадрат сумм
Мужской	Контроль
1 год
2 года
3 года
Женский	Контроль
1 год
2 года
3 года
Сумма квадратов				24248	68358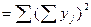
Квадрат сумм	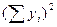			1994	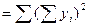4356

Воспользуемся данными таблицы и рассчитаем:

4. Определим число степеней свободы вариации:

Проведем предварительный анализ дисперсий, разделив суммы квадратов отклонений на соответствующее число степеней свободы (табл. 14):

Таблица 14 - Предварительный анализ дисперсий.

Источник вариации	Сумма квадратов отклонений	Степень свободы вариации	Дисперсия	Отношение дисперсий
Fфакт	Fтабл
Пол + стаж	22604,0		3229,1	32,4	2,77
Повторности	67,3		33,7	Х	Х
Остаточная	1394,7		99,6		Х
Общая	24066,0		X

5. По приложению А определяем F_табл. При 5% уровне вероятности для 7 и 14 степеней свободы .

.

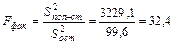Проведя предварительный анализ существенности средних (F_факт > F_табл ), делаем вывод о достоверности различий в средних и целесообразности перехода к дальнейшим расчетам.

6. Приступим к рассмотрению вариации реализованной литературы, которая характеризуется различиями по полу, стажу и их взаимодействием. Для этого, используя суммы отклонений по повторностям (табл. 12), составим вспомогательную таблицу:

Таблица 15 - Отклонения по вариантам опыта.

Пол	Контроль	Стаж работы, лет	Сумма
Мужской	-179	-88			-157
Женский	-13
Сумма	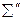-192	-36

7. Результаты вычислений возведем в квадрат и занесем в таблицу:

Таблица 16 - Таблица квадратов отклонений по вариантам опыта.

Пол	Контроль	Стаж работы, лет	Сумма	Квадрат суммы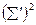
Мужской
Женский
Сумма						73754=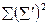
Квадрат сумм	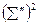				86968=	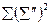4624=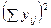

8. Полученная таблица квадратов позволяет установить:

(вычисление см. в п.3)

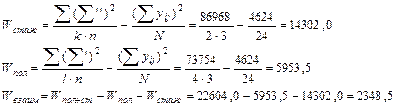
9. Определим число степеней свободы:

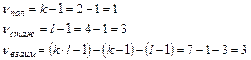
10. Перейдем к заключительному этапу анализа. Объединим результаты вычислений в общую таблицу:

Таблица 17 - Анализ дисперсий.

Источник вариации	Сумма квадратов отклонений	Степень свободы вариации	Дисперсия	Отношение дисперсий
Fфакт	Fтабл
Пол	5953,5		5953,5	59,7	4,60
Стаж	14302,0		4767,3	47,8	3,34
Взаимодействие факторов	2348,5		782,8	7,8	3,34
Повторности	67,3		33,7	0,3	3,74
Остаточная	1394,7		99,8	1,0	X
Общая	24066,0		X	X	X

Путем сопоставлений вычислим фактическое отношение дисперсий. За базу сравнения принимается 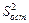. Например:

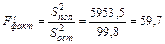и т.д.

По таблице 5%-го уровня распределения F (см. приложение А) установим F_табл (аналогично тому, как это было сделано в примере 2).

Сопоставление F_факт с F_табл показывает, что существенны различия в среднем количестве реализуемой литературы по первому и второму факторам. Значительно менялось количество литературы и в результате взаимодействия факторов. Таким образом, приходим к выводу, что выдвинутая гипотеза о том, что различия в количестве реализуемой литературы случайны, должна быть отвергнута.

Поскольку выдвинутая первоначально гипотеза на основании данных дисперсионного анализа отвергнута, следует оценить достоверность различий между парами средних.

Для этого вычислим среднюю и предельную ошибки.

шт / в месяц,

.

При вероятности 0,05 и 14 степенях свободы вариации критическое значение нормированного отклонения t (см. приложение Б) составляет 2,1448 ≈ 2,14.

Предельная ошибка:

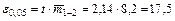шт. в месяц.

Следовательно, величина возможных случайных колебаний при данном уровне вероятности не должна превышать 17,5 шт. в месяц.

Определим существенность разности в количестве реализованной литературы.

Выполним следующие сопоставления (см. табл. 11).

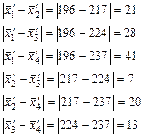
В первом блоке, который составили одни мужчины, все разности между средним количеством проданной литературы при меняющемся стаже работы существенны, так как превышают по абсолютной величине предельную ошибку ε _0,05=17,5 шт. в месяц.

Во втором блоке, представленном женщинами, две из шести разностей лежат в границах случайных колебаний. Несущественны разности 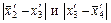то есть увеличение стажа работы с одного года до двух и с двух до трех дают соответственно разности в количестве проданной литературы 7 и 13 шт. в месяц, что меньше предельной ошибки.

Четыре из шести приведенных разностей больше 17,5 шт. в месяц и, следовательно, они существенны, а две – несущественны.

Таким образом, в рассмотренном примере, когда анализируется работа женщин, несколько ослабляется воздействие стажа на объем проданной литературы.

В целом же, в десяти случаях из двенадцати разности превышают по абсолютной величине предельную ошибку, что позволяет рассматривать их как существенные.