Этап 3. Итоговые результаты
Этап 1. Итоговые результаты.
Кратчайший путь к узлу 2 равен 7 миль (из узла 1),
Кратчайший путь к узлу 3 равен 8 миль (из узла 1),
Кратчайший путь к узлу 4 равен 5 миль (из узла 1).
Далее переходим ко второму этапу для вычисления кратчайших (накопленных) расстояний к узлам 5 и 6. Рассматривая узел 5 первым, из рис. 10.2 замечаем, что есть три возможных маршрута, по которым можно достичь узла 5, а именно (2, 5), [ (3, 5) и (4, 5). Эта информация вместе с кратчайшими расстояниями к узлам 2, 3, и 4 определяет кратчайшее (накопленное) расстояние к узлу 5 следующим образом.
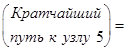
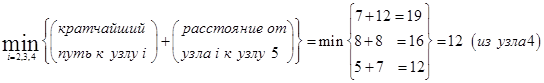
Аналогично для узла 6 имеем следующее.
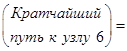
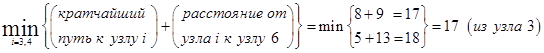
Этап 2. Итоговые результаты.
Кратчайший путь к узлу 5 равен 12 миль (из узла 4),
Кратчайший путь к узлу 6 равен 17 миль (из узла 3).
Последним шагом является третий этап. Конечный узел 7 можно достигнуть как из узла 5, так и 6. Используя итоговые результаты этапа 2 и расстояния от узлов 5 и 6 к узлу 7, получаем следующее:
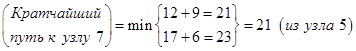
Этап 3. Итоговые результаты.
Кратчайший путь к узлу 7 равен 21 миле (из узла 5).
Привеленные вычисления показывают, что кратчайшее расстояние между узлами 1 и 7 равно 211 миле. Города, через которые проходит кратчайший маршрут, определяется следующим образом. Из готовых результатов третьего этапа следует, что узел 7 связывается с узлом 5. Далее из итоговых результатов второго этапа следует, что узел 4 связывается с узлом 5. Наконец, из готовых результатов первого этапа следует, что узел 4 связывается с узлом 1. Следовательно, оптимальным маршрутом является последовательность 1-4-5-7.
Теперь покажем, как рекуррентные вычисления динамического программирования можно выразить математически. Пусть 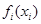 – кратчайшее расстояние до вершины
– кратчайшее расстояние до вершины 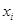 на этапе
на этапе 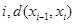 – расстояние от узла
– расстояние от узла 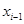 до узла
до узла 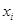 . Тогда
. Тогда 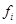 вычисляется из
вычисляется из 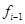 с помощью следующего рекуррентного уравнения.
с помощью следующего рекуррентного уравнения.
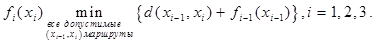
При i=1 полагаем 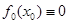 . Это уравнение показывает, что кратчайшие расстояния
. Это уравнение показывает, что кратчайшие расстояния 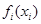 на этапе i должны быть выражены как функции следующего узла
на этапе i должны быть выражены как функции следующего узла 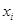 ,. В терминологии динамического программирования х, именуется состоянием системы на этапе
,. В терминологии динамического программирования х, именуется состоянием системы на этапе 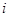 . В действительности состояние системы на этапе i — это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах. Такое определение состояния системы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.
. В действительности состояние системы на этапе i — это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах. Такое определение состояния системы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.
Определение состояния системы приводит к следующему унифицированному положению.
Принцип оптимальности. На каждом этапе оптимальная стратегия определяется независимо от стратегий, примененных на предыдущих этапах.
Применение принципа оптимальности демонстрируется вычислениями из примера 10.2-1. Например, на этапе 3 мы используем кратчайшие пути к узлам 5 и 6 и не интересуемся, как эти узлы были достигнуты из узла 1.
Упражнения 4.2,а
Решите задачу из примера 10.2-1 в предположении, что используются следующие длины маршрутов:
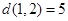 ,
, 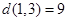 ,
, 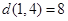 ,
,
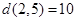 ,
, 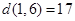 ,
,
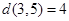 ,
, 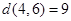 ,
,
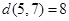 ,
,
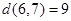 .
.
2.Я — заядлый турист. Прошлым летом мой друг и я отправились в пятидневный поход по прекрасным Белым Горам в штате Нью-Гемпшир. Мы решили ограничить наше путешествие территорией, на которой находится три хорошо известные вершины: Вашингтон, Джефферсон и Адаме. Гора Вашингтон имеет шестимильную тропу от подножия до вершины. Аналогичные тропы гор Джефферсона и Адамса имеют длину 4 и 5 миль соответственно. Тропы, соединяющие подножия этих трех гор, имеют следующую длину: 3 мили между вершинами Вашингтона и Джефферсона, 2 мили между вершинами Джефферсона и Адамса и 5 миль между вершинами Адамса и Вашингтона. В первый день мы стартовали от подножия вершины Вашингтона и вернулись в эту же точку к концу пятого дня. Нашей целью было пройти как можно более длинный путь. Мы также решили подниматься каждый день только на одну вершину и располагаться лагерем у подножия той горы, на которую мы решили восходить на следующий день. Кроме того, мы решили, что не будем подниматься на одну и ту же вершину в течение двух дней подряд. Каким было расписание нашего похода?
4.3. Рекуррентные алгоритмы прямой и обратной прогонки
В примере 4.2-1 вычисления проводились последовательно: от первого этапа до третьего. Такая последовательность вычислений известна как алгоритм прямой прогонки. Этот же пример может быть решен с помощью алгоритма обратной прогонки, в соответствии с которым вычисления проводятся от третьего этапа до первого.
Алгоритмы прямой и обратной прогонки приводят к одному и тому же решению. Несмотря на то, что алгоритм прямой прогонки представляется более логичным, в специальной литературе, посвященной динамическому программированию, неизменно используется алгоритм обратной прогонки. Причина этого в том, что в общем случае алгоритм обратной прогонки может быть более эффективным с вычислительной точки зрения. Продемонстрируем использование алгоритма обратной прогонки на примере 4.2-1. Мы также представим вычисления динамического программирования в компактной табличной форме.
Пример 3-1
Рекуррентное уравнение для алгоритма обратной прогонки в примере 4.2-1 имеет вид

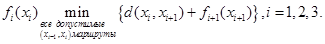
где 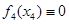 для
для 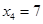 . Соответствующей последовательностью вычислений будет
. Соответствующей последовательностью вычислений будет 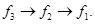
Этап 3. Так как узел 7 ( 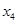 = 7) связан с узлами 5 и 6 (х3 = 5 и 6) в точности одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа можно подытожить следующим образом.
= 7) связан с узлами 5 и 6 (х3 = 5 и 6) в точности одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа можно подытожить следующим образом.
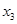 | 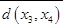 | Оптимальное решение | |
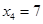 | 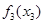 | 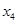 | |
Этап 2. Так как маршрута (2,6) не существует, соответствующая альтернатива не рассматривается. Используя значения 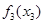 , полученные на третьем этапе, мы можем сравнить допустимые альтернативные решения, как показано в следующей таблице.
, полученные на третьем этапе, мы можем сравнить допустимые альтернативные решения, как показано в следующей таблице.
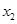 | 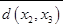 + + 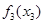 | Оптимальное решение | ||
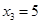 | 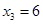 | 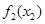 | 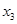 | |
| 12+9=21 | – | |||
| 8+9=17 | 9+6=15 | |||
| 7+9=16 | 13+6=19 |
Оптимальное решение второго этапа означает следующее. Если вы находитесь в узле (городе) 2 или 4, кратчайший путь к узлу 7 проходит через узел 5, а если находитесь в узле 3, кратчайший путь к узлу 7 проходит через узел 6.
Этап I. Из узла 1 мы имеем три альтернативных маршрута: (1,2), (1,3) и (1,4). Используя значения 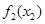 , полученные на втором этапе, вычисляем данные следующей таблицы.
, полученные на втором этапе, вычисляем данные следующей таблицы.
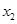 | 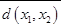 + + 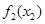 | Оптимальное решение | |||
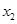 =2 =2 | 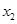 =3 =3 | 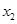 =4 =4 | 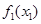 | 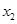 * * | |
| 7+21=28 | 8+15=23 | 5+16=21 |
Оптимальное решение на первом этапе показывает, что кратчайший путь проходит через город 4. Далее из оптимального решения на втором этапе следует, что из города 4 необходимо двигаться в город 5. Наконец, из оптимального решения на третьем этапе следует, что город 5 связан с городом 7. Следовательно, полным маршрутом, имеющим кратчайшую длину, является 1-4-5-7, и его длина равна 21 миле.
Упражнения 4. 3,а
1. Для задачи из упр. 4.2,а(1) получите рекуррентное соотношение обратной прогонки и используйте его для получения оптимального решения.
2. Для задачи из упр. 4.2,а(2) получите рекуррентное соотношение обратной прогонки и используйте его для получения оптимального решения.
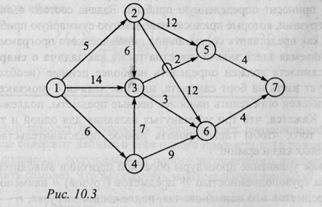
3. Определите кратчайший маршрут между городами 1 и 7 на сети дорог, представленной на рис. 10.3. Определите этапы и состояния системы с помощью алгоритма обратной прогонки, а затем решите задачу.
4.4. Некоторые приложения динамического программирования
В данном разделе рассмотрено четыре примера, каждый из которых выбран для демонстрации методов динамического программирования. При рассмотрении каждого примера особое внимание обратите на три основных элемента моделей динамического программирования. 1. Определение этапов.
2. Определение на каждом этапе вариантов решения (альтернатив).
3. Определение состояний на каждом этапе.
Из перечисленных выше элементов снятие состояния, как правило, представляется весьма сложным для восприятия. Рассмотренные в этом разделе приложения последовательно показывают, что определение состояния меняется в зависимости от моделируемой ситуации. При рассмотрении каждого приложения полезно ответить на следующие вопросы.
1. Какие соотношения связывают этапы вместе?
2. Какая информация необходима для того, чтобы получить допустимые решения на текущем этапе без повторной проверки решений, принятых на предыдущих этапах?
Мой опыт преподавания показывает, что понятие состояния удается глубже уяснить, если поставить под сомнение определение состояния, которое предложено в настоящей книге. Рекомендуем воспользоваться каким-либо другим определением, которое покажется вам "более логичным", и применить его в рекуррентных вычислениях. В конечном счете вы сможете убедиться, что приведенные здесь определения обеспечивают корректное решение задач. В то же время преложенный подход будет способствовать вашему пониманию самой концепции состояния.
Задача о загрузке
Задача о загрузке — это задача о рациональной загрузке судна (самолета, автомашины и т.п.), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки судна такими грузами, которые принося наибольшую суммарную прибыль.
Перед тем как представить соотношения динамического программирования, заметим, что рассматриваемая здесь задача известна также как задача о снаряжении, где пилот реактивного самолета должен определить наиболее ценные (необходимые) предметы, которые следует взять на борт самолет», или как задача о рюкзаке, в которой солдат (или турист) должен определить наиболее ценные предметы, подлежащие загрузке в ранец (рюкзак). Кажется, что три упомянутых названия для одной и той же задачи были выбраны для того, чтобы гарантировать равное представительство военно-морского флота, воздушных сил и армии.
Рекуррентное уравнение процедуры обратной прогонки выводится для общей задачи загрузки судна грузоподъемностью W предметов (грузов) п наименований. Пусть mi — количество предметов i-го наименования, подлежащих загрузке, r,- — прибыль, которую приносит один загруженный предмет i-го наименования, wi — вес одного предмета i-го наименования. Общая задача имеет вид. следующей целочисленной задачи линейного программирования.
Максимизировать 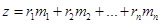
при условии, что
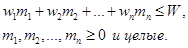
Три элемента модели динамического программирования определяются следующим образом.
1. Этап i ставится в соответствие предмету i-го наименования, 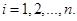
2. Варианты решения на этапе описываются количеством mi предметов i-го наименования, подлежащих загрузке. Соответствующая прибыль равна rimi. Значение тi заключено в пределах от 0 до 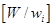 , где
, где 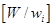 — целая часть числа
— целая часть числа 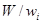
3. Состояние xi на этапе i выражает суммарный вес предметов, решения о погрузке которых приняты на этапах 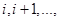 п. Это определение отражает тот факт, что ограничение по весу является единственным, которое связывает п этапов вместе.
п. Это определение отражает тот факт, что ограничение по весу является единственным, которое связывает п этапов вместе.
Пусть 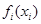 — максимальная суммарная прибыль от этапов
— максимальная суммарная прибыль от этапов 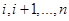 при заданном состоянии
при заданном состоянии 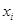 . Проще всего рекуррентное уравнение определяется с помощью следующей двухшаговой процедуры.
. Проще всего рекуррентное уравнение определяется с помощью следующей двухшаговой процедуры.
Шаг 1. Выразим 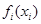 как функцию
как функцию 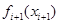 в виде
в виде
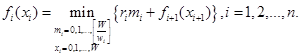
где 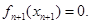
Шаг 2. Выразим 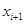 как функцию
как функцию 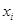 ,• для гарантии того, что левая часть последнего уравнения является функцией лишь
,• для гарантии того, что левая часть последнего уравнения является функцией лишь 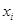 . По определению
. По определению 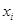 -
- 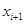 представляет собой вес, загруженный на этапе i т.е.
представляет собой вес, загруженный на этапе i т.е. 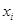 –
– 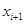
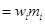 или
или 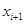 =
= 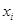 -
- 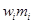 Следовательно, рекуррентное уравнение приобретает следующий вид.
Следовательно, рекуррентное уравнение приобретает следующий вид.
Пример 4.4-1
В 4-тонный самолет загружаются предметы трех наименований. Приведенная ниже таблица содержит данные о весе одного предмета 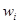 (в тоннах) и прибыли
(в тоннах) и прибыли 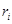 (в тысячах долларов), получаемой от одного загруженного предмета. Как необходимо загрузить самолет, чтобы получить максимальную прибыль?
(в тысячах долларов), получаемой от одного загруженного предмета. Как необходимо загрузить самолет, чтобы получить максимальную прибыль?
| Предмет i | 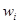 | 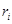 |
Так как вес одного предмета 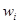 для всех наименований и максимальный вес W принимают целочисленные значения, состояние
для всех наименований и максимальный вес W принимают целочисленные значения, состояние 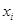 может принимать лишь целочисленные значения.
может принимать лишь целочисленные значения.
Этап 3. Точный вес, который может быть загружен на этапе 3 (предмет наименования 3), заранее неизвестен, но он должен принимать одно из значений 0,1,...,4 (так как W = 4 тонны). Состояния х3 = 0 и х3 = 4 представляют собой крайние случаи, когда предметы третьего наименования совсем не загружаются или загружают самолет полностью. Остальные значения х3 (= 1, 2 или 3) предполагают частичную загрузку самолета предметами третьего наименования. Действительно, при этих значениях х3 все оставшиеся емкости самолета могут быть заполнены предметами третьего наименования.
Так как вес w3 одного предмета третьего типа равен 1 тонне, максимальное количество единиц этого типа, которое может быть загружено, равно [4/1] = 4. Это означает, что возможными значениями х3 будут О, 1, 2, 3 и 4. Решение т3 является допустимым лишь при условии, что 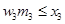 .Следовательно, все недопустимые альтернативы (те, для которых w3m3>x3) исключены. Следующее уравнение является основой для сравнения альтернатив на этапе 3.
.Следовательно, все недопустимые альтернативы (те, для которых w3m3>x3) исключены. Следующее уравнение является основой для сравнения альтернатив на этапе 3.
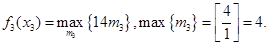
В следующей таблице сравниваются допустимые решения для каждого значения х3.
| х3. | 14 т3 | Оптимальное решение | |||||
| т3=0 | т3=1 | т3=2 | т3=3 | т3=4 | 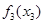 | т3 | |
| – | – | – | – | ||||
| – | – | – | |||||
| – | – | ||||||
| – | |||||||
Этап 2.
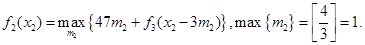
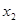 | 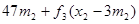 | Оптимальное решение | ||
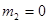 | 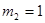 | 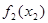 | 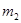 | |
| 0+0=0 | – | |||
| 0+14=14 | – | |||
| 0+28=28 | – | |||
| 0+42=42 | 47+0=47 | |||
| 0+56=56 | 47+14=61 |
Этап 1.



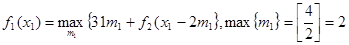
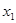 | 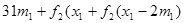 | Оптимальное решение | |||
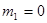 | 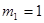 | 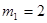 | 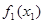 | 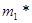 | |
| 0+0=0 | – | – | |||
| 0+14=14 | – | – | |||
| 0+28=28 | 31+0=31 | – | |||
| 0+47=47 | 31+14=45 | – | |||
| 0+61=61 | 31+28=59 | 62+0=62 |
Оптимальное решение определяется теперь следующим образом. Из условия W = 4 следует, что первый этап решения задачи при 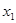 = 4 дает оптимальное решение
= 4 дает оптимальное решение 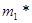 - 2, которое означает, что два предмета первого наименования будут загружены в самолет. Эта загрузка оставляет
- 2, которое означает, что два предмета первого наименования будут загружены в самолет. Эта загрузка оставляет 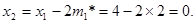 Решение на втором этапе при х2= 0 приводит к оптимальному решению
Решение на втором этапе при х2= 0 приводит к оптимальному решению 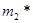 - 0, которое, в свою очередь, дает x3 = х2-3т2 =0-3
- 0, которое, в свою очередь, дает x3 = х2-3т2 =0-3 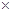 0=0. Далее этап 3 при х3=0 приводит к m3*=0. Следовательно, оптимальным решением задачи является m1*=2 m2*=0 m3*=0.Соответствующая прибыль равна 62 000 долларов.
0=0. Далее этап 3 при х3=0 приводит к m3*=0. Следовательно, оптимальным решением задачи является m1*=2 m2*=0 m3*=0.Соответствующая прибыль равна 62 000 долларов.
В таблице для первого этапа нам, по существу, необходимо получить оптимальное решение лишь для х1 = 4, так как это последний этап, подлежащий рассмотрению. Однако в таблицу включены также вычисления для х1 = 0,1,2 и 3, которые позволяют провести анализ чувствительности решения. Например, что произойдет, если максимальная грузоподъемность самолета будет 3 тонны вместо 4? Новое оптимальное решение может быть определено, начиная с х1 = 3 на первом этапе и продолжая так, как мы поступали при х1 = 4.
Задача о загрузке является типичным представителем задачи распределения ресурсов, в которой ограниченный ресурс распределяется между конечным числом видов (экономической) деятельности. При этом целью является максимизация соответствующей функции прибыли. В таких моделях определение состояния на каждом этапе будет аналогично приведенному для задачи о загрузке: состоянием на этапе 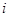 является суммарное количество ресурса, распределяемого на этапах
является суммарное количество ресурса, распределяемого на этапах 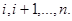
Упражнения 4. 4,а
1. В задаче примера 10.4-1 определите оптимальное решение, предполагая, что максимальная грузоподъемность самолета составляет 3 тонны.
2. Решите задачу о загрузке из примера 10.4-1 для каждого из следующих случаев.
· 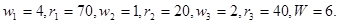
· 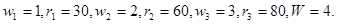
3. Турист собирается в путешествие по дикой местности и должен упаковать в рюкзак предметы трех наименований: пищу, средства первой помощи и одежду. Объем рюкзака составляет 3 кубических фута. Каждая единица пищи занимает 1 кубический фут, упаковка средств первой помощи — четверть кубического фута, а отдельный предмет одежды — примерно половину кубического фута. Турист определил свои предпочтения весовыми коэффициентами 3, 4 и 5 — для пищи, средств первой помощи и одежды соответственно. Это означает, что одежда является самым ценным предметом среди остальных. Опыт подсказывает туристу, что он должен взять не менее одного предмета каждого наименования и не более двух комплектов средств первой помощи. Сколько единиц каждого наименования возьмет турист в поход?
4. Студент должен выбрать 10 факультативных курсов на четырех различных факультетах, причем на каждом факультете должен быть выбран по меньшей мере один курс. Эти курсы распределяются между факультетами таким образом, чтобы максимизировать объем "знаний". Студент оценивает знания по шкале в сто баллов и приходит к выводам, представленным в следующей таблице.
| Факультет | Номер курса | ||||||
 7 7 | |||||||
| I | |||||||
| II | |||||||
| III | |||||||
| IV |
Какие курсы следует выбрать студенту?
5. У меня во дворе имеется небольшой огород 10 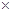 20 футов. Этой весной я собираюсь посадить овощи трех видов: помидоры, зеленые бобы и кукурузу. Огород разбит на ряды, длина которых равна 20 футам. Кукуруза и помидоры занимают ряды шириной 2 фута, а зеленые бобы — 3 фута. Помидоры мне нравятся больше, а бобы меньше. По 10-балльной шкале предпочтений я бы присвоил помидорам 10 баллов, кукурузе — 7 баллов и зеленым бобам — 3 балла. Независимо от моих предпочтений, жена настаивает, чтобы я посадил не менее одного ряда зеленых бобов и не более двух рядов помидоров. Сколько рядов каждого вида овощей следует мне посадить?
20 футов. Этой весной я собираюсь посадить овощи трех видов: помидоры, зеленые бобы и кукурузу. Огород разбит на ряды, длина которых равна 20 футам. Кукуруза и помидоры занимают ряды шириной 2 фута, а зеленые бобы — 3 фута. Помидоры мне нравятся больше, а бобы меньше. По 10-балльной шкале предпочтений я бы присвоил помидорам 10 баллов, кукурузе — 7 баллов и зеленым бобам — 3 балла. Независимо от моих предпочтений, жена настаивает, чтобы я посадил не менее одного ряда зеленых бобов и не более двух рядов помидоров. Сколько рядов каждого вида овощей следует мне посадить?
6. "Жилище для Человечества" — прекрасная благотворительная организация, которая строит дома для бедствующих семей силами добровольцев. Такая семья может выбрать себе дом из трех типоразмеров: 1000, 1100 и 1200 квадратных футов. Дом каждого типоразмера требует выполнения определенного объема работ силами добровольцев. Филиал организации в городе Файтвилл получил пять заявок на предстоящие шесть месяцев. Комитет по надзору дает оценку каждой заявке в численном виде, принимая во внимание различные факторы. Более высокая оценка означает более острую потребность в жилье. В течение предстоящих шести месяцев филиал организации в этом городе может привлечь к работе максимум 23 добровольца. Следующая таблица содержит оценку каждой заявки и необходимое число добровольцев для ее выполнения. Какие заявки следует утвердить комитету?
| Заявка | Размер дома (футов2) | Оценка | Необходимое число добровольцев |
7. Шериф округа Вашингтон принимает участие в переизбрании на следующий срок. Денежные средства на предвыборную кампанию составляют примерно 10000 долларов. Хотя комитет по переизбранию хотел бы провести кампанию во всех пяти избирательных участках округа, ограниченность денежных средств предписывает действовать по-другому. Приведенная ниже таблица содержит данные о числе избирателей и денежных средствах, необходимых для проведения успешной кампании по каждому избирательному участку. Каждый участок может либо использовать все предназначенные деньги, либо вовсе их не использовать. Как следует распределить денежные средства?
| Участок | Число избирателей | Необходимые средства ($) |
8. Конструируется электронный прибор, состоящий из трех основных компонентов. Все компоненты соединены последовательно, поэтому выход из строя одного из них влечет за собой отказ всего прибора. Надежность (вероятность безаварийной работы) прибора можно повысить путем дублирования каждого компонента. Конструкция прибора допускает использование одного или двух резервных (параллельных) блоков, т.е. каждый компонент прибора может содержать до трех блоков, соединенных параллельно. Следующая таблица содержит данные о надежности г и стоимости компонентов прибора.
| Число параллельных блоков | Компонент 1 | Компонент 2 | Компонент 3 | |||
 | 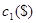 | 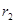 | 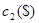 | 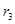 | 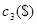 | |
| 0,6 | 0,7 | 0,5 | ||||
| 0,8 | 0,8 | 0,7 | ||||
| 0,9 | 0,9 | 0,9 |
Общая сумма, выделенная на конструирование прибора, равна 10000 долларов. Как следует сконструировать прибор? (Совет. Наша задача состоит в максимизации надежности 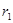
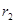
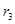 прибора. Это значит, что целевая функция является мультипликативной, а не аддитивной.)
прибора. Это значит, что целевая функция является мультипликативной, а не аддитивной.)
9. Решите следующую задачу с помощью метода динамического программирования.
Максимизировать 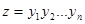
при условиях
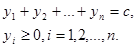
(Подсказка это упражнение аналогично предыдущему упражнению, но с той лишь разницей, что переменные 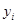 являются непрерывными)
являются непрерывными)
10. Решите следующую задачу с использованием метода динамического программирования
Минимизировать 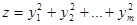
при условиях
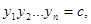
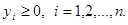
11. Решите следующую задачу посредством метода динамического программирования.
Максимизировать 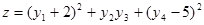
при условиях
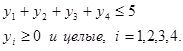
12. Решите следующую задачу с помощью метода динамического программирования.
Минимизировать 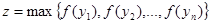
при условиях
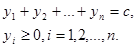
Найдите решение задачи при условии, что 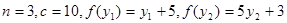 и
и 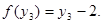
Задача планирования рабочей силы
При выполнении некоторых проектов число рабочих, необходимых для выполнения какого-либо проекта, регулируется путем их найма и увольнения. Поскольку как наем, так и увольнение рабочих связано с дополнительными затратами, необходимо определить, каким образом должна регулироваться численность рабочих в период реализации проекта.
Предположим, что проект будет выполняться в течение п недель и минимальная потребность в рабочей силе на протяжении 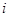 -й недели составит bi рабочих. При идеальных условиях хотелось бы на протяжении
-й недели составит bi рабочих. При идеальных условиях хотелось бы на протяжении 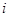 -й недели иметь в точности bi рабочих. Однако в зависимости от стоимостных показателей может быть более выгодным отклонение численности рабочей силы как в одну, так и в другую сторону от минимальных потребностей. Если
-й недели иметь в точности bi рабочих. Однако в зависимости от стоимостных показателей может быть более выгодным отклонение численности рабочей силы как в одну, так и в другую сторону от минимальных потребностей. Если 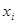 — количество работающих на протяжении
— количество работающих на протяжении 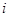 -й недели, то возможны затраты двух видов: 1)
-й недели, то возможны затраты двух видов: 1) 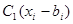 — затраты, связанные с необходимостью содержать избыток
— затраты, связанные с необходимостью содержать избыток 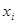 - bi рабочей силы и 2)
- bi рабочей силы и 2) 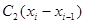 — затраты, связанные с необходимостью дополнительного найма
— затраты, связанные с необходимостью дополнительного найма 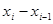 рабочих.
рабочих.
Элементы модели динамического программирования определяются следующим образом.
1. Этап i представляется порядковым номером недели 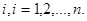
2. Вариантами решения на 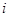 -м этапе являются значения xi — количество работающих на протяжении
-м этапе являются значения xi — количество работающих на протяжении 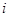 -й недели.
-й недели.
3. Состоянием на 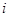 -м этапе является хi-1 — количество работающих на протяжении
-м этапе является хi-1 — количество работающих на протяжении 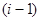 й недели (этапа).
й недели (этапа).
Рекуррентное уравнение динамического программирования представляется в виде
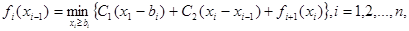
где. Вычисления начинаются с этапа п при хп =bn и заканчиваются на этапе 1.
Пример 4-2
Строительный подрядчик оценивает минимальные потребности в рабочей силе на каждую из последующих пяти недель следующим образом: 5, 7, 8, 4 и 6 рабочих соответственно. Содержание избытка рабочей силы обходится подрядчику в 300 долларов за одного рабочего в неделю, а наем рабочей силы на протяжении одной недели обходится в 400 долларов плюс 200 долларов за одного рабочего в неделю.
Выражая С1 и С2 в сотнях долларов, имеем следующее.
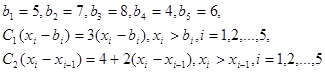
Этап 5. 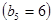 .
.
| x4 | 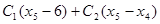 | Оптимальное решение | |
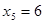 | 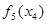 | x5 | |
| 3(0)+4+2(2)=8 | |||
| 3(0)+4+2(1)=6 | |||
| 3(0)+0=0 |
Этап 4. 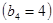
| x3 | 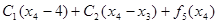 | Оптимальное решение | |||
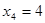 | 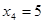 | 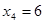 | 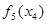 | 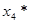 | |
| 3(0)+0+8=8 | 3(1)+0+6=9 | 3(2)+0+0=6 |
Этап 3. 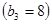
| x2 | 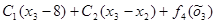 | Оптимальное решение | |
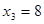 | 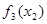 | 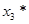 | |
| 3(0)+4+2(1)+6=12 | |||
| 3(0)+0+6=6 |
Этап 2. 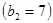
| x1 | 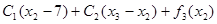 | Оптимальное решение | ||
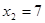 | 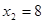 | 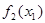 | 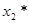 | |
| 3(0)+4+2(2)+12=20 | 3(1)+4+2(3)+6=19 | |||
| 3(0)+4+2(1)+12=18 | 3(1)+4+2(2)+6=17 | |||
| 3(0)+0+12=12 | 3(1)+4+2(1)+6=15 | |||
| 3(0)+0+12=12 | 3(1)+4+2=9 |
Этап 1. 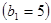
| x0 | 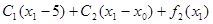 | Оптимальное решение | ||||
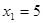 | 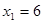 | 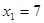 | 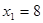 | 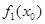 | 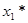 | |
| 0 | 3(0)+4+2(5) +19=33 | 3(1)+4+2(6) +17=36 | 3(2)+4+2(7) +12=36 | 3(2)+4+2(8) +9=35 | ||
Оптимальное решение определяется последовательно следующим образом.
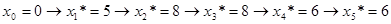 .
.
Полученному решению соответствует следующий план.
Номер недели ( 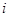 ) ) | Минимум рабочей силы ( 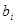 ) ) | Количество фактически работающих ( 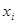 ) ) | Решение |
| Нанять 5 раочих | |||
| Нанять 3 рабочих | |||
| Ничего не менять | |||
| Уволить 2 рабочих | |||
| Ничего не менять |
Упражнения 4. 4,b
1. Решите задачу из примера 4-2 при следующих минимальных потребностях в рабочей силе.
a) 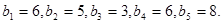
b) 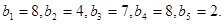
2. Пусть в примере 4-2 каждому уволенному рабочему выплачивается выходное пособие в размере 100 долларов. Найдите оптимальное решение задачи.
3. Туристическое агентство организовывает недельные поездки в Египет. В соответствии с договором на ближайшие четыре недели агентство должно обеспечить туристические группы арендными автомобилями в количестве семь, четыре, семь и восемь штук соответственно. Агентство заключает договор с местным дилером по прокату автомобилей. Дилер назначает арендную плату за один автомобиль 220 долларов в неделю плюс 500 долларов за любую арендную сделку. Агентство, однако, может не возвращать арендованные автомобили в конце недели, и в этом случае оно должно будет только арендную плату в 220 долларов. Каково оптимальное решение проблемы, связанной с арендой автомобилей?
4. Компания на следующие четыре года заключила контракт на поставку авиационных двигателей, по 4 двигателя в год. Доступные производственные мощности и стоимость производства меняются от года к году. Компания может изготовить пять двигателей за 1-й год, шесть— за 2-й, три— за 3-й и пять— за 4-й. Стоимость производства одного двигателя на протяжении следующих четырех лет равна соответственно 300 000, 330 000, 350 000 и 420 000 долларов. В течение года компания может произвести больше двигателей, чем необходимо, но в этом случае двигатели должны надлежащим образом храниться до их отгрузки потребителю. Стоимость хранения одного двигателя также меняется от года к году и оценивается в 20 000 долларов для первого года, 30 000 долларов — для второго, 40 000 долларов — для третьего и 50 000 долларов — для четвертого. В начале первого года компания имеет один двигатель, готовый к отгрузке. Разработайте оптимальный план производства двигателей.
5. Фирма выпускает пять типов электронных игр (Е1, Е2, ..., Е5) и пять типов механических игрушек (Ml, М2„..., М5). На рынке порядок предпочтения электронных игр таков: 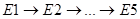 . Это означает, что клиент будет покупать игру с более высоким предпочтением, если она имеется в продаже. Известен также порядок предпочтения механических игрушек:
. Это означает, что клиент будет покупать игру с более высоким предпочтением, если она имеется в продаже. Известен также порядок предпочтения механических игрушек: 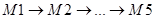 . Недельный спрос на пять типов электронных игр равен 100, 180, 90, 250 и 190 единиц соответственно. Аналогичные показатели для механических игрушек равны 300, 190, 240, 280 и 260 единиц соответственно. Производство одной игры Е1,Е2,...,Е5 обходится в 10, 12, 8, 9 и 6 долларов соответственно. Изготовление же одной игрушки Ml,Ml,...,М5 обходится фирме в 4, 5, 3, 2 и 3 доллара соответственно. Организация производства каждой электронной игры или игрушки обходится в 500 долларов. Определите оптимальный план производства игрушек.
. Недельный спрос на пять типов электронных игр равен 100, 180, 90, 250 и 190 единиц соответственно. Аналогичные показатели для механических игрушек равны 300, 190, 240, 280 и 260 единиц соответственно. Производство одной игры Е1,Е2,...,Е5 обходится в 10, 12, 8, 9 и 6 долларов соответственно. Изготовление же одной игрушки Ml,Ml,...,М5 обходится фирме в 4, 5, 3, 2 и 3 доллара соответственно. Организация производства каждой электронной игры или игрушки обходится в 500 долларов. Определите оптимальный план производства игрушек.
