Типовые примеры и методы их решения. Пример 1.3.1.В банк 6 мая предъявлен для учета вексель на сумму 14 тыс

Пример 1.3.1.В банк 6 мая предъявлен для учета вексель на сумму 14 тыс. руб. со сроком погашения 10 июля того же года. Банк учитывает вексель по учетной ставке 40% годовых, ис­пользуя способ 365/360. Определите сумму, которую получит

векселедержатель от банка, и комиссионные, удерживаемые банком в свою пользу за предоставленную услугу. За какое вре­мя до срока платежа операция учета векселя по учетной ставке 40% годовых имеет смысл?

Решение.Величина суммы, полученной векселедержателем,

рассчитывается по формуле (19) и при F = 14 тыс. руб., n= 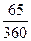года, d = 0,4 составит:

P = 14(1- 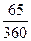0,4)=12,989 тыс. руб.

Дисконт D_d, полученный банком, представляет собой раз­ность между F (номинальной величиной векселя) и Р (дискон­тированной величиной векселя): D_d =14-12,989 = 1,011 тыс. руб.

Учет векселя по учетной ставке d имеет смысл, если п< ,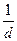

т.е. для данного случая n <2.5 года. Если n = 2,5 года, то Р = 14(1-2,5 0,4) = 0, т.е. владелец векселя вообще ничего не получит. При и > 2,5 сумма Р, которую должен получить при учете векселя его владелец, становится отрицательной, что не может иметь места.

Отметим, что поскольку 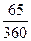40% = 7,22%, то комиссионные

360 D_d, полученные банком, представляют собой и 7,22% "во 100"

с 12,989 тыс. руб. Действительно, по формуле (8) получим:

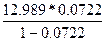= 1,011 тыс. руб.

Пример 1.3.2.Вексель на сумму 9 тыс. руб. учитывается по простой учетной ставке за 120 дней до погашения с дисконтом 600 руб. впользу банка. Определите величину этой годовой учетной ставки при временной базе, равной 360 дней в году.

Решение.Полагая в формуле (24) F = 9 тыс. руб., F- P = 0,6 тыс.py6. f = 120дней, Т = 360 дней,получим:

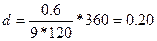
Таким образом, простая учетная ставка составляет 20% го­довых. Для проверки можно определить дисконт в пользу банка (т.е. решаем обратную задачу: по известной учетной ставке оп­ределяем дисконт):

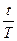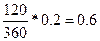F-P = F d = 9 тыс. руб.

Пример 1.3.3. Банк 7 июня учел три векселя со сроками по­гашения в этом же году соответственно 8 августа, 30 августа и 21 сентября. Применяя учетную ставку 25% годовых, банк удержал комиссионные в размере 2750 руб. Определите номи­нальную стоимость первых двух векселей, если номинальная стоимость второго векселя в два раза больше первого и третий вексель предъявлен на сумму 20 тыс. руб.

Решение, По таблице I приложения 2 находим, что первый вексель учтен за 62 дня до срока погашения, второй - за 84 дня и

третий - за 106 дней. Полагая F = 20 тыс. руб., п = 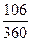года,

d = 0,25 , по формуле D_d = Fnd определим комиссионные, удер­жанные банком за согласие учесть третий вексель:

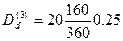= 1,472 тыс. руб.

Таким образом, общий дисконт от учета остальных двух векселей составит:

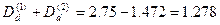тыс. руб

Обозначим теперь через F номинальную стоимость первого векселя, тогда номинальная стоимость второго векселя равна 2F. Следовательно,

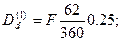
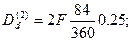
Поскольку в сумме эти дисконты доставляют 1,277 тыс оуб то, складывая их, получим уравнение:

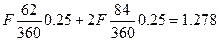
решая которое относительно F, находим

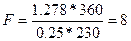тыс. руб

Отсюда получаем и номинальную стоимость второго векселя -

16 тыс. руб.

Пример 1.3.4. Вексель на сумму 18 тыс. руб., выданный 14 мая и сроком погашения 20 ноября этого же года, был учтен в банке 10 октября по учетной ставке 36% годовых способом 365/360. На номинальную стоимость векселя предусматривалось начисление простых процентов по процентной ставке 25% годо­вых способом 365/365. Найдите сумму, полученную векселе­держателем. Провести анализ дохода банка. Год високосный.

Решение. Поскольку на 18 тыс. руб. будут начислены про­стые проценты за 190 дней, то вначале по формуле (10) находим сумму, которая должна быть выплачена предъявителю векселя при его погашении:

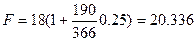тыс.руб.

Поскольку вексель был учтен за 41 день до срока погашения, то по формуле (19) владелец векселя получит сумму:

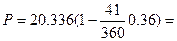19,502 тыс.руб.

В данном случае можно провести более глубокий анализ процесса учета векселя. Общий доход банка составит величину A = F-P = 20,336-19,502 = 0,834 тыс. руб. Этот доход складыва­ется из двух частей - проценты по векселю, причитающиеся за время, оставшееся до момента погашения векселя, и собственно комиссионные за предоставленную услугу.

Найдем срочную стоимость векселя в момент учета его банком:

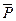= 18(1 + 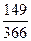0,25) = 19,832 тыс. руб.

Теперь можно определить проценты по векселю, состав­ляющие часть дохода банка:

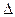_р = F- 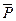= 20,336-19,832 = 0,504 тыс.руб.

Следовательно, собственно комиссионные, получаемые банком за услугу, оказываемую векселедержателю, составят величину:

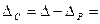0,834 - 0,504 = 033 тыс. руб.

Величину 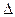_с можно было найти и по формуле 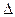_с = 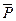- Р. С позиции банка сумма 330 руб. представляет собой плату за возможность более быстрого получения наличных векселедер­жателем. Отметим, что реальные потери векселедержателя со­ставляют именно величину 330 руб., а не 834 руб., как это ка­жется на первый взгляд. Конечно, банк может получить больше 330 руб., увеличивая учетную ставку.

Следует отметить, что если бы учетная ставка была, допус­тим, 30% годовых, а процентная - 40% годовых, то банк оказал­ся бы в проигрыше. Действительно, используя обозначения примера, получим:

F = 18(l + 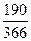0,4)=21,738 тыс.руб.;

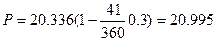тыс.руб.;

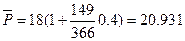тыс.руб.;

Поэтому банк потеряет величину:

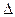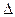_р - = Р- 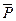=20,995-20,931 =0,064 тыс.руб.

Пример 1.3.5.В банк 15 февраля предъявлен для учета век­сель на сумму 40 тыс. руб. со сроком погашения 30 июня того же года. Банк учитывает вексель по простой процентной ставке 30% годовых. Определите сумму, полученную векселедержате­лем, и величину дисконта банка, если при учете использовался способ 365/365 и год високосный. Каковы будут определяемые величины при учете по простой учетной ставке 30% и использо­вании способа 365/360?

Решение.Если учет производится по простой процентной ставке, то, полагая в формуле (18) F = 40 тыс. руб., n = 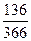года,

r = 0.3, находим сумму, полученную владельцем векселя:

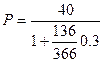= 35,988 тыс.руб.

Следовательно, дисконт банка составляет:

D_r =40-35,988 = 4,012 тыс.руб.

Если же учет производится по простой учетной ставке, то

пользуемся формулой (19) при F = 40 тыс. руб., n = 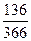года,

d = 0,3. В этом случае векселедержатель получит:

Р ₌ 40(1 - 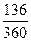0,3) = 35,467 тыс. руб.,

и поэтому дисконт банка составит:

D_d = 40 - 35,467 = 4,533 тыс. руб.

Таким образом, во втором случае векселедержатель получит на 521 руб. меньше, а банк - соответственно на 521 руб. больше.

Заметим, что если бы владелец векселя предъявил в банк вексель за 4 года до срока погашения, а банк учел вексель по простой процентной ставке, то векселедержатель получил бы:

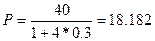тыс.руб

т.е. достаточно большую сумму, в то время как учет по простой учетной ставке 30% годовых за 4 года до срока погашения в принципе невозможен, так как для этой ставки верхней грани­цей является 10/3 года.

Обратим внимание и на следующий факт. Поскольку

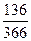30% = 11.148%, то комиссионные D_r , полученные банком,

представляют собой и 11,148% "на 100" с 40 тыс. руб. Действи­тельно, по формуле (7) получим:

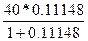= 4,012 тыс. руб.

Пример 1.3.6. За вексель, учтенный за 5 лет по учетной ставке 14% годовых, заплачено 4 тыс. руб. Определите номи­нальную величину векселя.

Решение. Ситуация, описанная в условии примера, равно­сильна следующей: на сумму 4 тыс. руб. в течение 5 лет осуще­ствляется наращение простыми процентами по простой учетной ставке 14% годовых . Необходимо опреднлить наращенную сумму . Поэтому можно воспользоваться формулой (20) в которой Р=4 тыс.руб., n=5 лет,d=0.14:

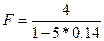= 13,333 тыс. руб.,

что и равно номинальной величине векселя.

Если же описанную ситуацию рассматривать с точки зрения процесса наращения, то приращение капитала в 4 тыс. руб. за 5 лет составит величину: Id =13,333-4 = 9,333 тыс. руб. Найдем приращение капитала за каждый год.

За первый год (п = 1) капитал увеличится на величину

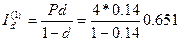тыс.руб

За два года (n = 2) капитал увеличится на величину

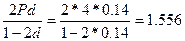тыс. руб.,

и, следовательно, его приращение за второй год составит:

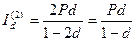= 1,556-0,651 = 0,905 тыс.руб.

Аналогичным образом получаем приращения за третий, чет­вертый и пятый годы:

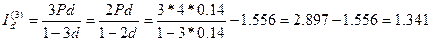
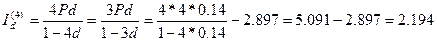
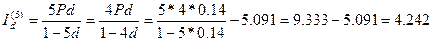
С целью проверки просуммируем полученные величины 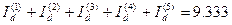тыс.руб т.е как и должно быть получим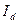

Пример 1.3.7. Найдите учетную ставку, эквивалентную про­стой процентной ставке 30% годовых, при наращении капитала: а) за год; б) за 150 дней. Временные базы ставок одинаковы.

Решение, а) Для расчета воспользуемся формулой (26), где r = 03, n = 1 год:

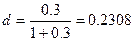
Таким образом, ученая ставка 23,08% годовых обеспечивает за год такое же наращение простыми процентами, как и про­центная ставка 30% годовых.

б) Здесь возможны три случая, когда в году 360, 365 или 366

дней, т.е. и n = 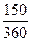года, п = 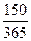года или п = 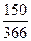года. Пользу-

ясь формулой (26), соответственно получаем:

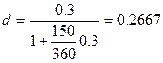
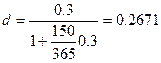
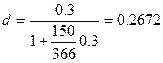
Если бы в слычае а) временные базы были бы неодинаковы , например , для учетнойт ставки -360 дней ,для процентной ставки -365 дней то следовало бы пользоваться формулой (28) где =365 дней =360 дней и t =150 дней

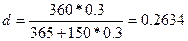
Пример 1.3.8. Предприниматель получил 12 марта ссуду в банке по простой учетной ставке 22% годовых и должен возвра­тить 15 августа того же года 30 тыс. руб. Определите различны­ми возможными способами сумму, полученную предпринима­телем, и величину дисконта, если год невисокосный и проценты ., удерживаются банком при выдаче ссуды. Какова будет доход­ность такой операции для банка в виде годовой простой про центной ставки?

Решение. Величина суммы, полученной предпринимателем, зависит от числа дней, которое берется в расчет. Точное число дней ссуды определяется, например, по таблице: 227 - 71 = 156 дней. Приближенное число дней состоит из 18 дней марта (30 -12); 120 дней (по 30 дней четырех месяцев: апрель, май, июнь, июль) и 15 дней августа. Т.е. приближенное число дней состав­ляет 18 + 120 + 15 = 153 дня. Теперь с помощью формулы (19) можно рассчитать возможные значения суммы Р, полученной предпринимателем, и величину дисконта Dd.

1. В расчет принимаются точные проценты и точное число дней ссуды:

Р = 30(1 - 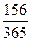0,22) = 27.179 тыс. руб.,

D_d =30-27,179 = 2,821 тыс. руб.

2. В расчет принимаются обыкновенные проценты и точное число дней ссуды:

Р = 30(1 - 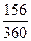0,22) =27.140 тыс. руб., 360

D_d = 30 - 27,140 = 2,860 тыс. руб.

3. В расчет принимаются обыкновенные проценты и прибли­женное число дней ссуды:

P = 30(1- 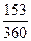0,22)=27Д95 тыс. руб., 360

D_d = 30 - 27,195 = 2,805 тыс. руб.

Для определения доходности для банка такой кредитной операции необходимо учитывать расчетное количество дней в году. Если для учетной и прояентной ставок используется одна и та же временная база, например 365 дней в году, и в расчет принимается точное число дней ссуды, то по формуле (25), по­лагая п = 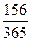года, d = 0,22, находим:

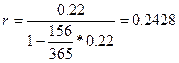
Таким образом, процентная ставка r=- 24,28% обеспечивает через 156 дней (считая, что в году 365 дней) получение такой же наращенной величины из начального капитала, что и учетная ставка d = 22%. Действительно,

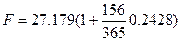= 30 тыс. руб.

В предположении, что в году 360 дней для точного ( n = )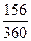

и приближенного (n = 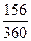) числа дней ссуды, соответственно

получим:

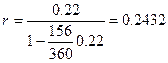
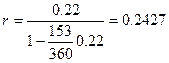
Если временные базы для процентной и учетной ставок раз­ные, то варианты расчета доходности для банка в виде годовой простой процентной ставки рассматриваются аналогичным об­разом. Например, полагая в формуле (27) Т_r = 365, T_d = 360, при

точном числе дней t= 156 находим:

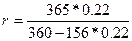= 0,2466.

Продолжая подобным образом, можно рассчитать г для всех возможных случаев. Конечно, формулу (27) можно было ис­пользовать и в случае одной и той же временной базы для про­центной и учетной ставок.

Пример 1.3.9.В банк предъявлен вексель на сумму 50 тыс. руб. за полтора года до срока его погашения. Банк согласен учесть вексель по переменной простой учетной ставке, установ­ленной следующим образом: первые полгода - 30% годовых, следующие полгода - 36% годовых, затем каждый квартал став­ка повышается на 2%. Определите дисконт банка и сумму, кото­рую получит векселедержатель.

Решение.Так как на первое полугодие установлена учетная ставка 30% годовых, то дисконт за этот период равен 50 * 0,5 * 03 тыс. руб. Дисконт за второе полугодие - 50 *0.5*0,36 тыс. руб. По­скольку на последующие кварталы установлены учетные ставки36% + 2% = 38% и 38% + 2% = 40% годовых, то дисконты равны соот­ветственно 50*0.25*0.38 тьтс.руб.и 50*0,25*0,4 тыс. руб.

Суммируя полученные величины, находим дисконт Dj за полтора года:

D_d =50(0.5*0.3+0.5*0.36+0.25*0.38+0.25*0.4) = 26.25 тыс. руб.

Следовательно, владелец векселя получит 50 - 26,25 = 23,75 тыс. руб.

Такой же дисконт D_d = 26,25 тыс. руб. можно было получить,

и установив на полтора года постоянную простую учетную ставку

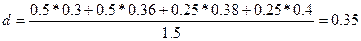
т.е. d= 35% годовых.

Пример 1.3.10.При учете предъявленного векселя на сумму 30 тыс. руб. за 40 дней до срока его погашения доход банка со­ставил 1,5 тыс. руб. Определите доходность этой финансовой операции для банка в виде простой годовой процентной ставки при расчетном количестве дней в году, равном 360.

Решение.Вначале находим сумму, выплаченную предъяви­телю векселя: Р = 30 -1,5 = 28,5 тыс. руб. Затем, полагая F - Р = 1,5 тыс. руб., t = 40 дней, Т = 360 дней, по формуле (23) получим:

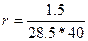360 = 0,4737, или 47,37%.

Решим этот пример другим способом, согласно которому вначале находим по формуле (24) простую годовую учетную ставку, по которой осуществлялся учет векселя:

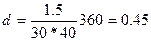
И после этого по формуле (27) определяем эквивалентную простую процентную ставку:

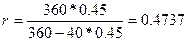
Естественно, получили тот же результат.

Пример 1.3.11. Депозитный сертификат дисконтного типа номиналом 300 тыс. руб. куплен за 100 дней до его погашения по цене, определяемой простой учетной ставкой 30% годовых, и через 40 дней продан по цене, определяемой простой учетной ставкой 28% годовых. Найдите доходность такой финансовой операции в виде простой годовой процентной ставки при расчет­ном количестве дней в году, равном 360. Какова будет доход­ность, если владелец сертификата продержит его до погашения?

Решение. Доход от приобретения депозитного сертификата дисконтного типа определяется тем, что он продается по цене ниже номинала, а погашается по номиналу. Также владелец та­кого сертификата может получить доход, продав сертификат до

даты его погашения.

Цену покупки депозитного сертификата находим по форму­ле (19) при F = 300 тыс. руб., t = 100 дней, T= 360 дней, d = 0,3 :

300(1 - 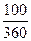0,3) =274,882 тыс.руб.

Поскольку позже депозитный сертификат был продан за 60 дней до срока погашения, то его цена продажи составила (t = 60 дней, d=02H):

300(l- 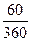0,28) = 286 тыс.руб.

Доходность такой операции кушш-продажи определяем по формуле (23), где P= 274,882 тыс. руб., F = 286 тыс. руб., t = 40 дней, T = 360 дней:

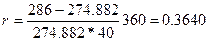или 36,40% годовых.

Следует заметить, что найденная доходность по существу не зависит от величины номинала данного депозитного сертифика­та, а зависит от размеров учетных ставок и сроков от момента покупки и продажи до момента погашения сертификата. Это хорошо видно при решении аналогичного примера в общем ви­де. Кстати, и этот пример можно было решать, полагая величину номинала депозитного сертификата произвольной величиной F, которая при нахождении доходности просто сократится. Если же сертификат не будет продан до срока погашения, то в этом случае доходность будет равна простой процентной став­ке, обеспечивающей через 100 дней получение такой же нара­щенной величины из начального капитала, что и учетная ставка ЗО% годовых, т.е. надо воспользоваться формулой (25):

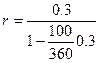= 03273, или 32,73% годовых.

Пример 1.3.12. Вексель учитывается банком за 120 дней до срока его погашения по простой учетной ставке 39% годовых. Определите доходность для банка такой финансовой операции в виде простой годовой процентной ставки, если: а) комиссион­ные не удерживаются; 6) удерживаются комиссионные в разме­ре 1% от суммы, выплачиваемой за вексель. Расчетное число дней в году принимается равным 360.

Решение, а) Пусть предъявлен вексель на некоторую сумму

120 F, тогда доход банка составит: F 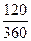0.39 = 0.13F, а предьявитель векселя получит сумму F~0,13F = 0,87F. Следовательно, по формуле (23) доходность для банка будет:

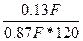360 = 0,4483,т.е.44,83%.

Очевидно, можно было и сразу применить формулу (27) при

T_r = Td = 360:

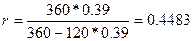
б) Так как сумма, выплачиваемая за вексель, равна O.87.F, то величину удержанных комиссионных определяем, взяв от этой суммы 1%: 0,87F* 0,01 = 0,0087F. Предъявитель векселя получит величину 0.87F - 0.0087F = 0.8613.F. Следовательно, общий доход банка составит: F-0,8613F = 0.1387F Теперь по формуле (23) можно определить доходность учета векселя для банка в виде простой годовой процентной ставки:

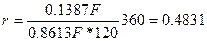т.е 48.31%

Таким образом, взимание комиссионных повышает доход-

ность учета для банка.

Задачи

1.3.1. Векселедержатель 20 февраля предъявил для учета вексель со сроком погашения 28 марта того же года. Банк учел вексель по учетной ставке 35% годовых и выплатил клиенту 19,3 тыс. руб. Какой величины комиссионные удержаны банком в свою пользу, если год невисокосный?

1.3.2. Векселедержатель предъявил для учета вексель на сумму 60 тыс. руб. со сроком погашения 21 октября текущего года. Вексель предъявлен 3 октября. Банк согласился учесть вексель с дисконтом в 26% годовых. Определите сумму, кото­рую векселедержатель получит от банка, и величину комисси­онных, удерживаемых банком в свою пользу за предоставлен­ную услугу. За какое время до срока платежа операция учета векселя по учетной ставке 26% имеет смысл?

1.3.3. Банк 9 июня учел два векселя со сроками погашения соответственно 29 июня и 23 июля того же года. Применяя учетную ставку 30% годовых, банк выплатил клиентам в общей сложности 34 216 руб. Определите номинальную стоимость первого векселя, если второй вексель предъявлен на сумму 10 тыс. руб.

1.3.4. Вексель на сумму 15 тыс. руб., выданный 3 апреля со сроком погашения 10 августа, был учтен в банке 11 июля по учетной ставке 26% годовых способом 365/360. На номиналь­ную стоимость векселя предусматривалось начисление простых процентов по процентной ставке 32% годовых способом 365/365. Найдите сумму, полученную векселедержателем.

1.3.5. Предприятие продало товар на условиях потребитель­ского кредита с оформлением простого векселя: его номиналь­ная стоимость - 1,8 млн. руб., срок векселя - 90 дней, простая процентная ставка за предоставленный кредит - 20% годовых. Через 60 дней с момента оформления векселя предприятие ре­шило учесть вексель в банке; предложенная банком простая го-довая учетная ставка составляет: а) 18%; 6) 25%. Рассчитайте сумму, получаемую предприятием, и комиссионные, получае­мые банком, если начисляются обыкновенные проценты.

1.3.6. Какой величины прибыль получит банк в результате учета 5 февраля по простой учетной ставке 30% годовых трех векселей, каждый из которых на сумму 15 тыс. руб., а сроки их погашения - 5 мая, 7 июня и 1 августа того же високосного года?

1.3.7. Вексель на сумму 80 тыс. руб. предъявлен в банке за 120 дней до срока его погашение. Банк учитывает вексель по простой процентной ставке 32% годовых. Определите дисконт, полученный банком, если при учете полагалось, что в году 360 дней. Какова была бы величина дисконта, если бы банк исполь­зовал простую учетную ставку 32% годовых?

1.3.8. В банк 13 июля предъявлен для учета вексель, выдан­ный 4 мая того же года и со сроком погашения 1 сентября, при­чем на номинальную стоимость векселя предусматривалось на­числение простых процентов по процентной ставке 35% годо­вых способом 365/365. Банк для определения своих комиссион­ных при учете векселя применяет простую процентную ставку 40% годовых и способ 365/360. Определите номинальную стои­мость векселя, если величина общего дохода банка составила 3521 руб.

1.3.9. Банк за 20 дней до срока учел вексель на сумму 40 тыс. руб., при этом удержав комиссионные в размере 800 руб. Какую учетную ставку использовал банк, еслн считается, что в году 360 дней? Как изменится результат, если банк при учете векселя ис­пользует простую процентную ставку?

1.3.10. Векселедержатель собирается предъявить какому-либо банку для учета вексель на сумму 50 тыс. руб. за 45 дней до срока его погашения. Один баше предлагает учесть вексель по учетной ставке 30% годовых. Другой банк предлагает учесть вексель по простой процентной ставке 30% годовых. Чьи усло­вия выгоднее для векселедержателя?

1.3.11. В банк предлагаются для учета два векселя: на сумму 30 тыс. руб. со сроком погашения через 2 месяца и на сумму 34 тыс. руб. со сроком погашения через 8 месяцев. При какой: а) учетной ставке, б) процентной ставке банк при учете этих век-

• селей выплатит одинаковые суммы, если расчетное число дней в году равно 360?

1.3.12. За вексель, учтенный за полтора года до срока по простой учетной ставке в 12%, заплачено 4,5 тыс. руб. Опреде­лите номинальную величину векселя.

1.3.13. Банк за 200 дней до срока учел вексель по учетной ставке 28% годовых и в тот же день продал этот вексель друго­му банку, который учел вексель по процентной ставке, также равной 28% годовых. В результате такой операции первый банк получил доход в 1,5 тыс. руб. Определите номинальную стои­мость векселя, если при любом учете предполагалось, что в году 360 дней.

1.3.14. Предприниматель разделил свой капитал на две рав­ные части, одну из них он поместил в банк под простую про­центную ставку 30% годовых, а другую часть потратил на по­купку векселя со сроком погашения через 250 дней, при этом он учел вексель по простой учетной ставке, также равной 30% го­довых. Через 250 дней деньги, полученные предпринимателем но векселю, превышали сумму, образовавшуюся к этому сроку в банке, на 572 руб. Какова была величина первоначального капи­тала предпринимателя, если во всех расчетах предполагалось, что в году 360 дней?

1.3.15. Дисконтный сертификат, выданный на 90 дней, обес­печивает держателю доход в виде дисконта, равного 18% от ве­личины номинала. Определите размер простой годовой учетной ставки, доставляющей такой же доход при наращении, если в году: а) 360 дней; б) 366 дней.

1.3.16. Предприниматель хочет получить ссуду в 50 тыс. руб. на полгода. Банк согласился предоставить ссуду на условиях начисления простых процентов по учетной ставке 24% годовых. Какую сумму предприниматель будет должен банку?

1.3.17. Банк выдал предпринимателю ссуду на полгода по простой учетной ставке 20% годовых, удержав проценты при выдаче ссуды. Определите сумму, полученную предпринимате­лем, и величину дисконта, если предприниматель должен воз­вратить 30 тыс. руб.

1.3.18. Клиент получил 14 апреля ссуду в банке по простой учетной ставке 25% годовых и должен возвратить 20 ноября того же года 10 тыс. руб. Определите различными возможными способами сумму, полученную клиентом, и величину дисконта, если год невисокосный и проценты удерживаются банком при выдаче ссуды. 1.3Л9. Клиент получил 10 февраля ссуду в банке по простой учетной ставке 30% годовых н должен возвратить весь долг 27 мая того же года. Какова будет доходность такой операции для банка в виде годовой простой процентной ставки, если год високосный и: а) временная база для учетной и процентной ставок одна и та же и равна числу дней в году; б) для учетной ставки временная база равна 360 дней, а для процентной ставки - 3 66 дней?

1.3.20. На капитал в 10 тыс. руб. в течение 4 лет осуществля­ется наращение простыми процентами по учетной ставке 12% годовых. Найдите приращение первоначального капитала за ка­ждый год и общую наращенную сумму.

1.3.21. Предприниматель получил в банке кредит на 60 дней по учетной ставке 30% годовых, при этом банком были удержа­ны комиссионные в размере 2% от величины кредита. Найдите доходность такой финансовой операции для балка в виде годо­вой простой процентной ставки, если банк начисляет простые проценты на исходную сумму кредита, полагая в году 360 дней. Как изменится доходность при выдаче кредита на 30 дней и на 90 дней?

1.3.22. На какой срок необходимо поместить имеющуюся денежную сумму под простую процентную ставку 34% годовых, чтобы она увеличилась в 1,5 раза? Как изменится ответ, если наращение осуществляется по простой учетной ставке 34% го­довых?

1.3.23. На какой срок необходимо поместить имеющуюся денежную сумму под простую процентную ставку 40% годовых, чтобы начисленные проценты были в 1,2 раза больше первона­чальной суммы? Как изменится ответ, если наращение осущест­вляется по простой учетной ставке 40% годовых?

1.3.24. Найдите простую учетную ставку, эквивалентную простой процентной ставке 20% годовых, при наращении капи­тала за невисокосный год. Рассмотрите случаи одинаковых и разных временных баз.

1.3.25. Депозитный сертификат дисконтного типа сроком на 45 дней продается по цене, определяемой простой учетной став­кой 32% годовых и расчетным количеством дней в году, равным 360. Определите эквивалентное значение простой годовой про­центной ставки, определяющей стоимость привлеченных средств банка, при расчетном количестве дней в году, равном 365.

1.3.26. Депозитный сертификат дисконтного типа номина­лом 400 тыс. руб. куплен за 150 дней до его погашения по цене, определяемой простой учетной ставкой 34% годовых, и через 90 дней продан по цене, определяемой простой учетной ставкой 30% годовых. Найдите доходность такой финансовой операции в виде простой годовой процентной ставки при расчетном коли­честве дней в году, равном 360. Какова будет доходность, если владелец сертификата продержит его до погашения? Влияет ли на доходность величина номинала этого сертификата?

1.3.27. Какая простая процентная ставка при учете векселя (по формуле математического дисконтирования) за 60 дней до срока погашения эквивалентна учетной ставке при коммерче­ском учете, если учетная ставка равна: а) 10%, б) 20%, в) 50% годовых? Временные базы при использовании ставок одинаковы и равны 360 дней.

1.3.28. Банк учитывает вексель за 180 дней до срока по учет­ной ставке 34% годовых, используя временную базу в 360 дней. Определите доходность такой операции в виде простой годовой процентной ставки при временной базе, равной 365.

1.3.29. При учете предъявленного векселя на сумму 150 тыс. руб. за 200 дней до срока его погашения доход банка составил 24 тыс. руб. Определите: а) доходность этой финансовой опера­ции для банка в виде простой годовой процентной ставки; б) по какой простой учетной ставке был учтен вексель. Расчетное число дней в году принимается равным 360.

1.3.30. Вексель на сумму 50 тыс. руб., выданный 1 июня и сроком погашения 1 сентября того же года, был учтен в банке 2 августа по учетной ставке 32% годовых. На номинальную стоимость векселя предусматривалось начисление простых процентов по процентной ставке 30% годовых. Определите в виде простой годовой процентной ставки доходность этой финансовой операции для предъявителя векселя и для банка, если и яри учете, и при наращении берутся в расчет точные проценты с точным числом дней и год невисокосный. Зависит ли величина доходности от суммы, написанной на векселе? Зависит ли величина доходности финансовой операции для банка от процентной ставки, по которой начисляются простые проценты? 1.3.31. В банк предъявлен вексель за 280 дней до срока пла­тежа. Какова должна быть простая годовая учетная ставка, ис­пользуемая банком, чтобы доходность операции учета в виде простой процентной ставки составляла 40% годовых? Расчетное количество дней в году равно 360.

1.3.32. Банк использует при выдаче кредитов простую про­центную ставку 45% годовых для расчетного количества дней в году, равном 365. За 70 дней до срока погашения в банк предъ­явлен вексель. Какую простую учетную ставку должен исполь­зовать банк, полагая в году 360 дней, чтобы обеспечить равенст­во доходностеЙ операции учета и кредитных операций?

1.3.33. Вексель учитывается банком за 80 дней до срока его погашения по простой учетной ставке 35% годовых. Определите доходность для банка такой финансовой операции в виде про­стой годовой процентной ставки, если: а) комиссионные не удерживаются; б) удерживаются комиссионные в размере 2% от суммы, выплачиваемой за вексель. Расчетное число дней в году принимается равным 360.

1.3.34. Вексель, до срока оплаты которого осталось 140 дней, учтен в банке по простой учетной ставке 38% годовых при рас­четном количестве дней в году, равном 360. Доходность опера­ции учета в виде простой годовой процентной ставки составила: а) 44,59%; б) 45,33%. Определите, какое при этом принималось расчетное количество дней в году.

1.3.35. На сумму 20 тыс. руб. начисляются с начала года простые проценты по учетной ставке 30% годовых. Определите наращенную сумму на конец первого квартала, если ежемесячно проводится операция реинвестирования, начисляются точные проценты с точным числом дней и год високосный. Какова была бы наращенная сумма в случае непроведения операции реинве­стирования?

1.3.36. В банк предъявлен вексель на сумму 80 тыс. руб. за полгода до срока его погашения. Банк согласен учесть вексель по переменной простой учетной ставке, установленной следую­щим образом: первые два месяца - 24% годовых и затем в каж­дом следующем месяце ставка повышается на 1,5%. Определите дисконт банка и сумму, которую получит векселедержатель. Можно ли воспользоваться постоянной учетной ставкой, дос­тавляющей такой же дисконт?

1.3.37. За какое время до срока погашения необходимо предъявить для учета вексель на сумму 1000 руб., чтобы резуль­таты учета по простой процентной ставке 30% годовых и по простой учетной ставке 30% годовых отличались меньше чем на одну копейку? Временные базы при использовании ставок оди­наковые.