Типовые примеры и методы их решения. Пример 2.3.1.Рассчитайте накопленную сумму для различ­ных вариантов начисления сложных процентов за один год (равный 360 дням)

Пример 2.3.1.Рассчитайте накопленную сумму для различ­ных вариантов начисления сложных процентов за один год (равный 360 дням), если исходная сумма Р = 1000 руб. и номи­нальная годовая процентная ставка 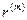= 30%. Рассмотрите случаи, когда проценты начисляются один раз, по полугодиям, ежеквартально, ежемесячно, ежечасно, ежеминутно, ежесекунд­но и непрерывно. Для каждого случая определите эффективную годовую процентную ставку.

Решение. Результаты, полученные для всех вариантов, при­ведем в виде таблицы, причем в четвертом столбце вычислены разности между наращениями с данным числом начисления процентов и базовым, а в пятом столбце указаны разности меж­ду наращенными суммами двух соседних строчек.

I

	Частота начисления		Наращение
P		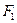	базовое	цепное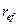
	Ежегодное (т = 1)		-	-	0,3
	Полугодовое (т = 2)	1322,5	22,5	22,5	0,3225
	Ежеквартальное {т = 4)	1335,47	35,47	12,97	0,33547
	Ежемесячное (т = 12)	1344,89	44,89	9,42	0,34489
	Ежедневное (ш = 360)	1349,69	49,69	4,8	0,34969
	Ежечасное (т = 8640)	1349,85	49,85	0,16	0,34985
	Ежеминутное (т = 518400)	1349,86	49,86	0,01	0,34986
	Ежесекундное (т = 31104000)	1349^6	49,86		0,34986
	Непрерывное (т = оо)	1349,86	49,86		0,34986

Накопленную сумму и эффективную процентную ставку во всех случаях, кроме последнего, находим соответственно по формулам (58) и (63). При непрерывном начислении процентов получим:

F₁ =Pe 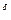-1000-e^0,3 =1349,86 руб.,

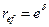-1= 1,34986 -1 = 034986.

Как и следовало ожидать, приведенные расчеты подтвер­ждают наличие прямой зависимости между частотой начисле­ния процентов и накопленной суммой; пятый столбец таблицы показывает, что с увеличением частоты начисления темп при­роста накопленной суммы уменьшается. Если считать с точно­стью до копеек (что и имеет смысл при практических расчетах и как сделано при заполнении таблицы), то замечаем, что начис­ление сложных процентов каждую минуту (или за меньший пе­риод) доставляет ту же сумму, что и непрерывное начисление процентов. Даже начисление каждый час дает наращенную сумму лишь на 1 копейку меньше.

Эффективная процентная ставка с ростом частоты начисле­ния сложных процентов растет и в пределе достигает величины 34,986%.

Пример 2.3.2.На сумму 6 тыс. руб. в течение 5 лет начис­ляются непрерывные проценты. Определите наращенную сум­му, если сила роста равна: а) 7%; б) 27%.

Решение,а) Полагая Р = 6 тыс. руб.₍ п = 5, 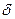= 0,07, по фор-ле (78) получим:

F₅ = 6е^0,07*5 = 8,514 тыс. руб.

Если в данном случае применить формулу (55), т.е. осущест­влять начисление обычных сложных процентов по процентной ставке г = 0,07, то получим сумму:

F₅ =6(l + 0,07)⁵ =8,415 тыс. руб.,

которая отличается от предыдущей всего на 99 руб., хотя нара­щение происходит достаточно долго - 5 лет. Такой результат объясняется небольшой величиной ставки. Ясно, что при более частом начислении сложных процентов эта разница будет еще меньше.

6) Так как в этом случае 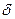= 027, то

F₅ = 6е^0,27*5 =23,145 тыс. руб.

Если же воспользоваться формулой (55) при r = 0,27, то по­лучим:

F₅=6(l + 0,27)⁵ =19,823 тыс. руб.,

т.е. имеем значительную разницу (3,322 тыс. руб.) между най­денными суммами.

Пример 2.3.3.Какую сумму необходимо поместить на бан­ковский депозит, чтобы при непрерывном начислении процентов по ставке 25% получить 30 тыс. руб. через: а) 4 года; б) 9 лет?

Решение,а) Для определения искомой суммы воспользуемся формулой (78). Полагая n = 4 , F_n = F₄ = 30 тыс. руб., 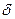= 0,25 , из этой формулы получим:

Р = 30e^-0,25*4 = 30е^-1 = 11,036 тыс. руб.

б) Поскольку и « 9, то

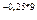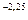P=30e =30e =3,162 тыс.руб.

Пример 2.3.4.За какой срок сумма 10 тыс. руб. достигнет величины 25 тыс. руб. при непрерывном начислении процентов и силе роста 28% за год?

Решение.Полагая в формуле (79) F_n = 25 тыс. руб.,

Р = 10 тыс. руб., 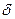= 0,28, находим:

n=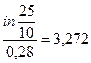

Если бы начислялись сложные проценты, например, по годовой номинальной процентной ставке r 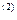= 0,28, то по фор­муле (60):

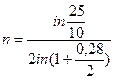= 3,497года,

т.е., естественно, получили больший срок, чем при непрерывном начислении процентов.

Пример 2.3.5. Банк выдает ссуду на 7 лет под сложную про­центную ставку 36% годовых с начислением процентов каждые полгода. Какую непрерывную ставку должен установить банк, чтобы за 7 лет получить тот же доход?

Решение. Пусть Р - величина ссуды, тогда при использова­нии процентной ставки банк получит через 7 лет (согласно фор­муле (58)):

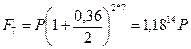
Теперь для определения силы роста можно воспользоваться формулой (80):

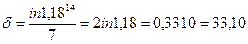
Конечно, этот пример можно было решить, и воспользовав­шись сразу формулой (97), связывающей эквивалентные силу роста и сложную процентную ставку.

Пример 2.3.6. Банк предоставил кредит на 4 года под непре­рывную ставку 30% за год. Определите доходность такой фи­нансовой операции для банка в виде: а) простой годовой про­центной ставки; б) годовой эффективной процентной ставки.

Решение, а) Если Р - величина кредита, то через n = 4 года наращенная сумма, которую заемщик должен будет возвратить, составит: Поэтому доходность в виде простой годовой процентной ставки составит (по формуле (23)):

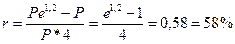
Обратим внимание, что в данном случае по существу была применена формула (93).

б) При определении r 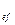воспользуемся формулой (64):

r_ef = 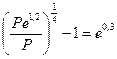-1 = 0,3499 = 34,99% .

Заметим, что годовая эффективная процентная ставка r_еf, и

сила роста S связаны соотношением: r 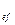= e 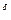— 1, которым мы

фактически и воспользовались при решении примера.

Пример 2.3.7.Предприниматель получил в банке ссуду на 6 лет по непрерывной ставке 25% за год, при этом банком были удержаны комиссионные в размере 2% от величины ссуды. Оп­ределите доходность такой финансовой операции для банка в виде: а) простой годовой процентной ставки; б) годовой эффек­тивной процентной ставки, если непрерывные проценты начис­ляются на исходную величину ссуды.

Решение,а) Обозначим через Р величину ссуды, тогда ве­личина удержанных комиссионных составит 0,02P и господину N будет выдана сумма Р - 0,02Р = 0.98Р . Через 6 лет господин N должен будет вернуть (согласно формуле (78)) сумму, равную

Ре^0,25*6 = Ре^1,5 . Банк вычисляет доходность сделки исходя из ус­ловия: наращенная по простой процентной ставке r на реально выданную ссуду сумма 0,98Р(1+6r) должна быть равна возвра­щаемой господином N через 6 лет сумме Ре^1,5. Таким образом, доходность сделки r определяется из уравнения: 0,98P(1 + 6r) = Ре^1,5. Откуда:

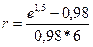= 0,5955 = 59,55%.

По существу воспользовались формулой (23).

б) В этом случае- наращенная по эффективной процентной ставке r_ef на реально выданную ссуду сумма составит 0,98P(1+r 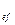) 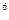и, следовательно, получим уравнение: 0,98P(1+r 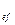)⁶= Pe^1,5, откуда:

r 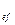= = 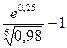0,2884 = 28,84%.

Пример 2.3.8.На вклад 16 тыс. руб. начисляются непрерыв­ные проценты. Определите наращенную сумму за 6 лет, если интенсивность наращения изменяется следующим образом: в первые два года она равна 20%, в следующие три года - 24% и в последний год - 26%. Какую постоянную силу роста необхо­димо взять, чтобы за 6 лет получить такую же наращенную сумму?

Решение.Пусть Р = 16 тыс. руб. По формуле (78) за первые два года при силе роста 5 = 0,2 наращенная сумма составит:

F₂=l6e^0,2*2 =16е^0,4 тыс. руб.

Далее наращение суммы F₂ непрерывными процентами за три года при 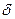= 0,24 обеспечит величину:

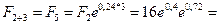16e^1,12 тыс. руб.

И наконец, за последний год получим при 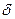= 0,26:

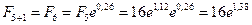=63,598 тыс. руб.

Такую же наращенную сумму за 6 лет можно получить, если в качестве постоянной силы роста взять

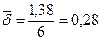
Заметим, что 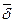представляет собой взвешенную сумму ис­ходных непрерывных ставок, где весом для каждой ставки явля­ется доля времени (от общего срока 6 лет), в течение которого использовалась данная ставка. Действительно:

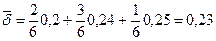
Пример 2.3,9.Господин N намеревается обменять имеющиеся у него немецкие марки и поместить полученную сумму на рублевом депозите сроком на 2 года под ставку 21% годовых с непрерывным начислением процентов, после чего наращен­ную сумму опять конвертировать в немецкие марки. При каком ожидаемом курсе продажи не имеет смысла такая финансовая операция, если курс покупки немецких марок на начало срока составляет 10 руб. 64 коп. и на валютном депозите денежную сумму можно поместить под процентную ставку 18% годовых с ежеквартальным начислением сложных процентов?

Решение.Обозначим через Р имеющуюся первоначальную сумму немецких марок, через К - ожидаемый курс продажи немецких марок через 2 года, при котором нет смысла в двой­ном конвертировании. Неизвестную величину К находим, при­равнивая наращенные суммы на валютном и на рублевом депо­зитах с учетом конвертации:

P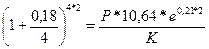

отсюда К= 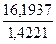= 11,39 руб. Если ожидаемый курс продажи будет менее 11 руб. 39 коп., то финансовая операция, связанная с двойной конвертацией, целесообразна.

Пример 2.3.10.Сумма 15 тыс. руб. была помещена в банк на некоторый срок, по истечении которого на эту сумму были на­числены непрерывные проценты с силой роста 30% за год. По­сле уплаты налога на проценты величина наращенной суммы составила 36,2 тыс. руб. Определите срок, за который было осуществлено наращение, если ставка налога на проценты равна 12% и налог на все полученные проценты был выплачен один раз в конце срока.

Решение.Воспользуемся соотношением (101), разрешая его относительно п :

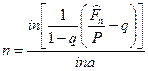
Так как в этом случае Р = 15 тыс. руб., 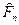=36,2 тыс. руб., q=0,12 ,a=e⁰³ ,in= 0,3 то

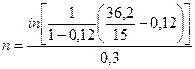= 3,193 года.

С целью проверки применим непосредственно формулу (101):

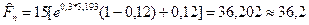тыс. руб.

Пример 2.3.11.Сумма 15 тыс. руб. была помещена в банк на некоторый срок, в течение которого на сумму начислялись не­прерывные проценты с силой роста 30% за год. После уплаты налога на все начисленные проценты величина итоговой нара­щенной суммы составила 36,2 тыс. руб. Определите срок, в те­чение которого осуществлялось наращение, если ставка налога на проценты равна 12% и налог на проценты уплачивается каж­дый год путем выделения средств из накапливаемой суммы.

Решение. Выражая из равенства (102) л, в обозначениях предыдущего примера находим;

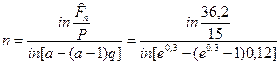= 3,282 года,

т.е. получен больший по величине срок, чем в предыдущем случае.

Задачи

2.3.1. На сумму 12 тыс. руб. в течение 6 лет начисляются не­прерывные проценты. Определите наращенную сумму, если сила роста равна: а) 6%; б) 16%; в) 26%.

2.3.2. Рассчитайте наращенную сумму для различных вари­антов начисления процентов за один год (равный 360 дням) по сложной учетной ставке, если исходная сумма равна 1000 руб. и номинальная годовая учетная ставка составляет 20%. Рассмот-

211риге случаи, когда проценты начисляются один раз в год, по по­лугодиям, ежеквартально, ежемесячно, ежечасно, ежеминутно, ежесекундно и непрерывно- Для каждого случая определите эф­фективную годовую учетную ставку.

2.3.3. Клиент поместил в банк 40 тыс. руб. на 2 года. Какая сумма будет на счете клиента, если банк начисляет сложные проценты: а) по номинальной процентной ставке 30% годовых с полугодовым начислением процентов; б) по номинальной учет­ной ставке 30% годовых с ежеквартальным начислением про­центов; в) по непрерывной ставке с силой роста 30% за год?

2.3.4. Какую сумму необходимо поместить на банковский депозит, чтобы через 5 лет получить 80 тыс. руб., если происхо­дит непрерывное начисление процентов по ставке 22%?

2.3.5. Известно, что современная стоимость 10 тыс. руб., ко­торые один клиент должен получить по банковскому депозиту через 2 года, равна удвоенной современной стоимости 6 тыс. руб., .которые должен получить другой клиент по банковскому депозиту через 4 года. В обоих случаях используются непре­рывные проценты и одна и та же непрерывная ставка. Чему рав­на эта ставка?

2.3.6. За какой срок сумма 50 тыс. руб. достигнет величины 90 тыс. руб. при непрерывном начислении процентов и силе роста 34%? Как изменится ответ при начислении сложных про­центов ежеквартально по номинальной процентной ставке 34% годовых?

2.3.7. Заемщик должен уплатить кредитору по векселю сле­дующие суммы: 15 тыс. руб. на 1 января 1999 г.; 20 тыс. руб. на 1 января 1998 г.; 30 тыс. руб. на 1 октября 1998 г. Определите приведенную стоимость долга на моменты: а) 1 января 1995 г.; б) 1 июля 1997 г., если используется непрерывное начисление процентов с силой роста 12% за год.

2.3.8. Банк выдает ссуду на 9 лет под сложную процентную ставку 32% годовых с начислением процентов каждый квартал. Какую непрерывную ставку должен установить банк, чтобы за 9 лет получить тот же доход? Изменится ли полученный резуль­тат, если срок ссуды будет 3 года?

2.3.9. Банк предоставил кредит на 6 лет под непрерывную ставку 27% за год. Определите доходность такой финансовой операции для банка в виде: а) простой годовой процентной ставки; б) годовой эффективной процентной ставки.

2.3.10. Предоставлена ссуда на 5 лет под непрерывную став­ку. Определите величину этой ставки, если доходность сделки для кредитора в виде годовой эффективной процентной ставки составила 38%. Зависит ли величина искомой непрерывной ставки от срока ссуды?

2.3.11. Предприниматель может получить ссуду либо на ус­ловиях ежеквартального начисления сложных процентов по процентной ставке 36% годовых, либо на условиях непрерывно­го начисления процентов с интенсивностью 34% за год. Какой вариант предпочтительнее для предпринимателя?

2.3.12. Вкладчик хотел бы за 6 лет увеличить в 2,5 раза сум­му, помещаемую в банк на депозит. Какова должна быть сила роста, если банк начисляет непрерывные проценты? Какова должна быть сила роста, чтобы обеспечить увеличение поме­щаемой суммы в 4 раза?

2.3.13. Оцените, что лучше: получить 20 тыс. руб. через 3 года или 68 тыс. руб. через 7,5 года, если можно поместить деньги на депозит под непрерывную ставку 28% за год?

2.3.14. Под какую непрерывную ставку можно поместить деньги на депозит, если 10 тыс. руб. сейчас эквивалентны 30 тыс. руб. через 4 года? Какая сложная процентная ставка с на­числением процентов по полугодиям решает эту задачу?

2.3.15. Определите время, за которое происходит удвоение первоначальной суммы при начислении непрерывных процен­тов, если сила роста равна: а) 5%; б) 25%; в) 50%; г) 100%.

2.3.16. Определите современную ценность 60 тыс. руб., если:

а) эта сумма будет получена через 2 года 6 месяцев; б) эта сумма была получена 4 года 6 месяцев назад; в) эта сумма получена в настоящий момент времени. Учесть возможность помещения денег на депозит под непрерывную процентную ставку 30%.

2.3.17. Банк начисляет непрерывные проценты с силой роста 27%. Определите современную ценность 20 тыс. руб., если: а) эта сумма была помещена на депозит в банке 3 года 4 месяца назад;

б) эта сумма будет помещена на депозит в банке через 2 года 9 месяцев.

2.3.18. Некоторый капитал помещен в банк под непрерыв­ную ставку 30%. Через 2 года и 3 месяца счет был закрыт и по­лучена сумма 189,755 тыс. руб. Определите величину наращен­ной суммы, которая была бы получена через полтора года. 2.3.19. Господин N поместил в банк 10 тыс. руб. на условиях начисления непрерывных процентов с силой роста 28%. Через 15 месяцев господин N снял со счета 4 тыс. руб., еще через 2 года положил на свой счет 3 тыс. руб., а после этого через 2 года 6 ме­сяцев он закрыл счет. Определите сумму, полученную господи­ном N при закрытии счета.

2.3.20. Вкладчик положил в банк 8 тыс. руб. на условиях на­числения непрерывных процентов с силой роста 26%. Через полтора года вкладчик снял со счета 5 тыс. руб., а через 2 года после этого он положил 7 тыс. руб. Еще через 2 года 6 месяцев вкладчик положил такую сумму, что на его счете еще через год оказалось 60 тыс. руб. Определите, какую сумму вкладчик по­ложил последний раз.

2.3.21. Вкладчик открыл счет в банке, положив некоторую сумму денег. Такую же по величине сумму он добавлял на свой счет еще три раза: через 1 год 6 месяцев, 2 года 6 месяцев и 4 года после открытия счета. Через 5 лет на счете вкладчика бы­ло 80 тыс. руб. Какую сумму вносил вкладчик каждый раз, если банк начисляет непрерывные проценты с силой роста 30%?

2.3.22. Предприниматель взял в банке кредит на сумму 150 тыс. руб. на условиях начисления непрерывных процентов с силой роста 30%. Через полтора года он вернул банку 60 тыс. руб., но еще через полгода взял кредит в сумме 50 тыс. руб. Через 2 года после этого предприниматель вернул полностью получен­ные кредиты. Какую сумму предприниматель при этом вьтлатил банку?

2.3.23. Определите, какую сумму необходимо поместить в банк, начисляющий непрерывные проценты с силой роста 24%, чтобы иметь возможность снять через 2 года 15 тыс. руб. и еще 20 тыс. руб. через 3 года после этого, полностью исчерпав счет.

2.3.24. Предприниматель приобрел оборудование стоимо­стью 300 тыс. руб. в кредит под непрерывную ставку 22% годо­вых. Через 2 года он уплатил 180 тыс. руб., а еще через полтора года полностью погасил долг. Определите, какую сумму пред­приниматель при этом выплатил.

2.3.25. За взятые в долг деньги под непрерывную ставку 25% годовых должник обязан уплатить кредитору 40 тыс. руб. 1 июля 1997 г. Какую сумму необходимо уплатить должнику, если он вер­нет долг: а) 1 января 1997 г.; б) 1 января 1998 г.; в) 1 июля 1999 г.?

2.3.26. Предприниматель получил в банке ссуду на 7 лет по непрерывной ставке 28% за год, при этом банком были удержа­ны комиссионные в размере 1,5% от величины ссуды. Опреде­лите доходность такой финансовой операции для банка в виде: а) простой годовой процентной ставки; б) годовой эффективной процентной ставки, если непрерывные проценты начисляются на исходную величину ссуды.

2.3.27. Выдается ссуда по непрерывной ставке 22% годовых, при этом взимаются комиссионные в размере 1% от величины ссуды."" Непрерывные проценты начисляются на исходную вели­чину ссуды. На какой срок должна быть выдана ссуда, чтобы доходность такой сделки для кредитора в виде годовой эффек­тивной процентной ставки составляла 28%?

2.3.28. При выдаче кредита на 3 года по непрерывной ставке 24% годовых были удержаны комиссионные. Непрерывные про­центы начислялись на исходную величину кредита. Сколько про­центов составили комиссионные от величины кредита, если до­ходность такой финансовой операции для кредитора в виде эф­фективной процентной ставки получилась равной 30% годовых?

2.3.29. На вклад 6 тыс. руб. начисляются непрерывные про­центы. Найдите наращенную сумму за 8 лет, если интенсив­ность наращения изменяется следующим образом: в первые три года она равна 12%, в следующие два года - 14% и в каждый оставшийся год увеличивается на 3%. Какую постоянную силу роста необходимо взять, чтобы за 8 лет получить такую же на­ращенную сумму?

2.3.30. Сумма 25 тыс. руб. помещена в банк под непрерыв­ную ставку с силой роста 20% за год. В конце каждого года 3% от наращенной к этому моменту суммы расходуется. Определи­те величину наращенной суммы в конце десятого года после осуществления всех расходов.

2.3.31. На сумму 10 тыс. руб. в течение 3 лет начисляются не­прерывные проценты с силой роста 34% за год, причем в конце каждого года расходуется часть наращенной к этому моменту суммы: в конце первого года - %, в конце второго года- У_А, в конце третьего - /₅. Определите величину наращенной суммы в конце третьего года после осуществления всех расходов.

2.3.32. Господин N обменивает 2000 долл. на рубли и полу-^ченную сумму помещает на 15 месяцев на рублевый депозит под.

непрерывную ставку 24%. Определите наращенную сумму в дол­ларах, если курс покупки долларов на начало срока составляет 19 руб. 60 коп., курс продажи в конце срока - 21 руб. 30 коп.

2.3.33. Господин N намеревается обменять имеющиеся у не­го доллары США и поместить полученную сумму на рублевом депозите сроком на 1 год 6 месяцев под ставку 22% годовых с непрерывным начислением процентов, после чего наращенную сумму опять конвертировать в доллары США. При каком ожи­даемом курсе продажи не имеет смысла такая финансовая опе­рация, если курс покупки долларов на начало срока составляет 19 руб. 54 коп. и на валютном депозите денежную сумму можно поместить под процентную ставку 16% годовых с ежемесячным начислением сложных процентов?

2.3.34. Как лучше поступить с имеющейся в наличии неко­торой суммой немецких марок: поместить на один год на ва­лютный депозит под процентную ставку 18% годовых с еже­квартальным начислением сложных процентов или поместить на рублевый депозит под ставку 20% с непрерывным начисле­нием процентов? Курс покупки немецких марок на начало срока составляет 10 руб. 40 коп., ожидаемый курс продажи через год -11 руб. 20 коп.

2.3.35. Сумма 50 тыс. руб. была помещена в банк на некоторый срок, по истечении которого на сумму были начислены сложные проценты по годовой номинальной процентной ставке 30% исходя из: а) ежегодной схемы начисления; б) ежеквартальной схемы на­числения; в) непрерывной схемы начисления. После уплаты налога на проценты величина наращенной суммы составила 124,88 тыс. руб. Определите срок, за который было осуществлено наращение, если ставка налога на проценты равна 15% и налог на все получен­ные проценты был выплачен один раз в конце срока.

2.3.36. Некоторый капитал был помещен в банк на 3 года 6 ме­сяцев, по истечении которых на этот капитал были начислены не­прерывные проценты с силой роста 24% за год и счет был закрыт. После уплаты налога на проценты наращенный капитал стал равен 129,504 тыс. руб. Определите величину первоначального капитала, если налог на все полученные проценты выплачивается один раз в конце срока и ставка налога на проценты равна 12%.

2.3.37. Некоторый капитал был помещен в банк на 2 года 6 месяцев на условиях начисления раз в год непрерывных про­центов с силой роста 30% за год, и в конце срока счет был закрыт. После уплаты налога на все начисленные проценты итого­вый наращенный капитал стал равен 76,688 тыс. руб. Определи­те величину первоначального капитала, если налог на проценты уплачивается каждый год путем выделения средств из накапли­ваемой суммы и ставка налога на проценты равна 15%.

2.3.38. На какой срок необходимо поместить имеющуюся денежную сумму под непрерывную процентную ставку 32% с однократным начислением в конце срока непрерывных процен­тов, чтобы эта сумма увеличилась в 3 раза с учетом уплаты на­лога на проценты, если ставка налога на проценты равна 15% и налог на все полученные проценты выплачивается один раз в конце срока?

2.3.39. На какой срок необходимо поместить имеющуюся де­нежную сумму на условиях начисления раз в год непрерывных процентов с силой роста 34% за год, чтобы эта сумма увеличилась в 4 раза с учетом уплаты налога на проценты, если налог на про­центы уплачивается каждый год путем выделения средств из нака­пливаемой суммы и ставка налога на проценты равна 12%?

2.4. Эквивалентность ставок

Основные положения

• Один и тот же финансовый результат можно получить раз­личными способами, используя различные ставки, методы на­ращения и дисконтирования.

• Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые отношения сторон не ме­няются. Таким образом, участникам финансового соглашения безразлично, какая ставка будет фигурировать в контракте.

• При выводе равенств, связывающих эквивалентные ставки, используется следующая идея: если из первоначального капита­ла наращением за данное время необходимо получить некото­рую сумму, то будут эквивалентными все ставки, обеспечиваю­щие один и тот же множитель наращения. Поэтому приравнивая друг к другу множители наращения, получим соотношения ме-жду эквивалентными ставками. Точно так же при переходе от будущей стоимости к приведенной стоимости с помощью дис­контирования приравниваются множители дисконтирования.

• Эквивалентные ставки, подобно эффективным ставкам, по­зволяют сравнивать между собой финансовые контракты, усло­вия которых различны.

• Формулы, связывающие эквивалентные простые и сложные ставки, зависят от продолжительности периода начисления. Формулы, связывающие эквивалентные сложные ставки, не за­висят от продолжительности периода начисления.

• Переход от дискретных ставок к соответствующим эквива­лентным непрерывным ставкам позволяет упростить анализ многих сложных финансовых задач. Осуществив необходимые математические выкладки, полученные результаты можно пред­ставить опять в любых удобных эквивалентных дискретных ставках, являющихся более привычными.

• Проблему эквивалентности ставок можно рассматривать и с более общих позиций, например эквивалентность одной став­ки нескольким ставкам или эквивалентность двух наборов ста­вок и т.п.

Вопросы для обсуждения

1. Можно ли с помощью двух различных ставок получить один и тот же финансовый результат? Поясните на примере.

2. Можно ли сказать, что любая ставка характеризует доходность финансовой операции?

3. Какие ставки называют эквивалентными?

4. Почему участникам финансового соглашения безразлично, какая из эквивалентных ставок указывается в контракте?

5. Можно ли рассматривать определение эффективной ставки (процентной или учетной) как определение одной из эквива­лентных ставок?

6. Какая идея используется при выводе равенств, связывающих эквивалентные ставки?

7. В каких случаях эквивалентность процентных ставок не зави­сит от продолжительности периода начисления?

8. В каких случаях эквивалентность процентных ставок зависит от продолжительности периода начисления?

9. Для каких целей переходят от дискретных ставок к соответ­ствующим эквивалентным непрерывным ставкам?

10.Приведите пример ситуации, когда ставка эквивалентна двум ставкам.