Номинальная процентная ставка

Сложные проценты могут начисляться несколько раз в году

( например, по месяцам, по кварталам, по полугодиям ). Для рассмотрения этого случая введем понятие номинальной ставки.

Номинальная ставка- это годовая ставка, проценты по которой начисляются m раз в году (m > 1). Обозначим ее через j . Следовательно, за один период проценты начисляются по ставке j / m.

Пример.Если по номинальной ставке j = 20 % происходит начисление 4 раза в год, то ставка за один период (квартал ) будет равна

20 % :4 = 5%.

Формулу (8) теперь можно представить следующим образом:

S = P ( 1 + j / m )^N, (10)

где N - общее количество периодов начисления, N= m×t, t - количество лет. С ростом частоты m начислений в году коэффициент наращения и, следовательно, абсолютный годовой доход растут.

Эффективная процентная ставка

Для сравнения реального относительного дохода за год при начислении процентов один и m раз, введем понятие эффективной ставки процентов.

Эффективная годовая ставка процентов i_эф - это ставка, измеряющая реальный относительный доход, который получают в целом за год от начисления процентов, т. е. i_эф - это годовая ставка сложных процентов, которая дает тот же результат, что и m - разовое начисление процентов по ставке за период i = j/ m .

Эффективная ставка находится из условия равенства двух соответствующих коэффициентов наращения за один год:

1 + i_эф = ( 1 + j / m )^m.

Отсюда следует, что

i_эф = ( 1 + j / m ) ^m - 1(11)

Пример. Определите эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки j=18 %, при ежеквартальном начислении процентов (m=4).

Решение. Из формулы (11) получаем:

i_эф = ( 1 + 0,18 / 4 )⁴ - 1 = 0, 1925 ( или 19, 25 %).

Пример. Найдите эффективную ставку, если номинальная ставка равна 25 % при ежемесячном начислении процентов.

Решение. i_эф = ( 1 + 0,25 / 12 )¹² - 1 = 0,2807 или 28,07 %.

Для сторон в сделке безразлично, применить ставку 25 % (при помесячном начислении) или годовую ставку 28,07 %.

Пример.Найдите номинальную процентную ставку, проценты по которой начисляются по полугодиям, эквивалентную номинальной ставке 24% с ежемесячным начислением процентов.

Решение. Пусть j₂- процентная ставка, соответствующая начислению по полугодиям, j₁₂ - по месяцам.

Из равенства коэффициентов наращения получаем:

( 1 + j₂ / 2 )² = ( 1 + j₁₂ / 12 )¹²,

отсюда

1 + j₂ / 2 = ( 1 + j₁₂ / 12 )⁶ Þ j₂ = 2[( 1 + j₂ / 12 )⁶ - 1] =

= 2 [( 1 + 0,24/12)⁶ - 1 ] = 0,25 или j₂= 25 %.

Непрерывное начисление процентов

Сумма, наращенная за t лет по формуле (10) при постоянной процентной ставке j_m с увеличением числа m увеличивается, но при неограниченном возрастании m сумма S = S_m стремится к конечному пределу.

Действительно

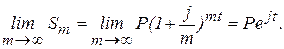Этот факт дает основание применять непрерывное начисление процентов по годовой ставке d. При этом наращенная сумма за время t определяется формулой

S = Pe^{d t}. (12)

Процентная ставка d называется силой роста.

Пример. Банк начисляет проценты по непрерывной ставке d=8 % на сумму 20 тыс. руб. в течение 5 лет. Найти наращенную сумму.

Решение. Из формулы (12) следует, что наращенная сумма

S = 20 000 e^0,08×5 = 20 000 × e^0,4 = 20 000 × 1,49182 = 29 836,49 руб.

Задачи

3.1. Сумма 400 тыс. руб. инвестируется на 2 года под 30 % годовых. Найдите наращенную сумму и сложные проценты за этот срок.

3.2.Кредит размером 500 тыс. руб. выдан под сложные проценты на 1 год по ставке 10 % в месяц. Вычислите полную сумму долга к концу срока.

3.3. Определите сложные проценты за полтора года, начисленные на 70 тыс. руб. по ставке 5 % за квартал.

3.4.На срочный вклад в банке зачислено $200 по ставке 6 % годовых. Найдите накопленные на счете суммы через 2, 3, 4 и 5 лет при условии начисления: а) простых процентов; б) сложных процентов; в) непрерывных процентов.

3.5.Рассчитайте эффективную процентную ставку, эквивалентную номинальной ставке 36 %, при ежемесячном начислении процентов. Ответ: 42,6 %.

3.6. Для номинальной ставки 12 % с начислением процентов два раза в год вычислите эквивалентную ставку, проценты по которой начисляются ежемесячно.

УЧЕТ ИНФЛЯЦИИ

В современных условиях инфляция часто играет решающую роль, и без ее учета конечные результаты представляют собой весьма условную величину. В реальной жизни инфляция проявляется в падении покупательной способности денег и общим уровнем повышения цен. Следовательно, ее необходимо учитывать при проведении финансовых операций. Рассмотрим способы ее учета.

Темпы инфляции измеряются с помощью системы индексов инфляции, которые характеризуют среднее изменение уровня цен для некоторого фиксированного набора (корзины) товаров и услуг за определенный период времени. Пусть стоимость корзины в момент времени t равна S(t).

Индексом цен или индексом инфляции J_P за время от t₁ до t₂ называется безразмерная величина

J_P = S( t₁) / S( t₂ ),

атемпом инфляции за этот период называется относительный прирост цен:

h =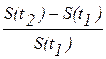 =J_P - 1.

Отсюда индекс цен

J_P = 1 + h.

Если срок рассмотрения инфляции включает в себя n периодов, в каждом из которых средний темп инфляции равен h,то

J_P = (1 + h)ⁿ.

В случае, когда темп инфляции в i-ом периоде равен h_i , индекс инфляции за n периодов вычисляется по формуле

J_P = (1 + h₁) (1 + h₂)…(1 + h_n).

Индекс инфляции J_Pпоказывает во сколько раз, а темп инфляции h- на сколько процентов выросли цены за рассматриваемый период.

Индекс покупательной способности денег J_D равен обратной величине индекса цен:

J_D = 1 / J _P = 1/ ( 1 + h).

Пример. Вы имеете сумму в 140 тыс. руб. Известно, что за два предшествующих года цены выросли в два раза, т.е. индекс цен J_P = 2. В этом случае индекс покупательной способности денег равен J_D = 1/2. Значит, реальная покупательная способность 140 тыс. руб. составит в момент получения всего 140 × 1/2 = 70 тыс. руб. в деньгах двухлетней давности.

Если h - годовой темп инфляции, то годовой индекс цен равен 1 + h, поэтому наращенная сумма с учетом инфляции

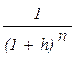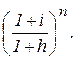S _и = P ( 1 + i )ⁿ = P (13)

Очевидно, что если среднегодовой темп инфляции hравен ставке процентов i, то S_и = P, т.е. роста реальной суммы не произойдет: наращение будет поглощаться инфляцией. Если h > i , то реальная сумма меньше первоначальной. Только в ситуации h < i происходит реальный рост.

Пример.Постоянный темп инфляции на уровне 10% в месяц за год приводит к росту цен в размере J_P = 1,1¹² = 3,14. Таким образом, годовой темп инфляции h = J_P - 1 = 2,14 или 214%.

В целях уменьшения воздействия инфляции и компенсации потерь от снижения покупательной способности денег используется индексация процентной ставки. При этом ставка корректируется в соответствии с темпом инфляции.

Скорректированная ставка называется брутто-ставкой.Вычислим эту ставку, обозначив ее через r.

Если компенсируется инфляция в размере брутто-ставки при наличии простых процентов, то величину rнаходим из равенства множителей наращения:

1 + n× r = ( 1 + n × i ) J_P = ( 1 + n × i )( 1 + h ) ⁿ ,

Отсюда

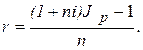(14)

Величину брутто-ставки для наращения по сложной процентной ставке находим из равенства (n = 1):

1 + r = ( 1 + i )( 1 + h ),

тогда

r = i + h + h×i (15)

Формулы (14), (15) означают следующее: чтобы обеспечить реальную доходность в i %, при темпе инфляции h нужно назначить ставку в размере r %.

Пример.Банк выдал на 6 месяцев кредит - 5 млн руб. Ожидаемый месячный уровень инфляции – 2 %, требуемая реальная доходность операции равна 10 % годовых. Определите ставку процентов по кредиту с учетом инфляции, размер наращенной суммы и величину процентного платежа.

Решение. Индекс инфляции J_P = (1 + 0,02)⁶ = 1,1262. Из (14) получим величину брутто-ставки:

r = 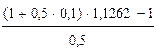=0,365 (или 36,5 % ).

Размер наращенной суммы

S= P(1 + n r ) = 5 (1 + 0,5×0,365 ) = 5,9126 млн. руб.

Величина процентного платежа ( плата за кредит )

I = 5,9126 - 5,0 = 0,9126 млн. руб.

Пример.Кредит в 1 млн. руб. выдан на два года. Реальная доходность должна составлять 11% годовых (сложные проценты). Расчетный уровень инфляции 16% в год. Определите ставку процента при выдаче кредита, а также наращенную сумму.

Решение. Из формулы (15) имеем:

r = 0,11+0,16+ 0,11× 0,16 = 0,2876;

S = 1,0 ( 1 + 0,2876 )² = 1,658 млн. руб.

Задачи

4.1. Кредит 500 тыс. руб. выдается с 20.06.98г. по 15.09.98г. При выдаче кредита считается, что индекс цен к моменту его погашения составит 1,3. Определите брутто-ставку и погашаемую сумму.

Ответ: R = 134% ; S _R = 658 194 руб.

4.2.Кредит в размере 5 млн руб. выдается на 3 года. Реальная доходность операции должна составлять 3 % годовых по сложной ставке. Расчетный уровень инфляции составляет 10% в год. Вычислите брутто-ставку и погашаемую сумму. Ответ: R = 13,3 % ; S_кR = 7 272 098 руб.

4.3.В банк помещен вклад в сумме 100 тыс. руб. под 100 % годовых сроком на 5 лет. Ожидаемый в течение этого периода темп инфляции h = =50 % в год. Определите реальную сумму, которую будет иметь клиент по истечении пяти лет: а) с учетом инфляции; б) без учета инфляции.

4.4.Какую ставку должен назначить банк, чтобы при годовой инфляции 11% реальная доходность оказалась 6 %.

ФИНАНСОВЫЕ РЕНТЫ

Обычная годовая рента

Финансовые операции часто предполагают не разовые платежи, а некоторую их последовательность во времени. Примером могут служить погашение займа, арендная плата и т.д. Такие последовательности платежей называютпотоком платежей.

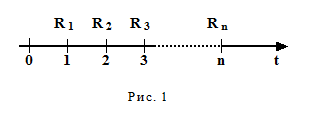
Пусть финансовая операция по договору начинается в момент t_0, а заканчивается в момент t_n . Выплаты R_k (k = 1,2,..,n) происходят в моменты t_k. Обычно полагают t₀ = 0 (рис. 1).

Финансовой рентой называется последовательность периодических выплат R_k , R _k > 0 , осуществляемых через равные промежутки времени.

Выплаты R_k называют членами ренты. Если все выплаты одинаковы, т.е. R_k = R , то рента называется постоянной.

Пусть d- период ренты, а n - число выплат, тогда произведение периода на число выплат nd представляет собой календарный срок ренты. Если выплата производится в конце каждого периода (рис. 1), то рента называется обычной, а если в начале периода, то приведенной (рис. 2).

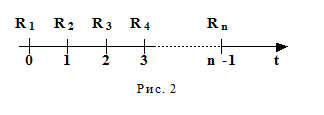
Выбирая базовуюединицу времени, зададим процентную ставку ренты (сложную). Найдем наращенную сумму S обычной годовой ренты, состоящей из n выплат, т.е. сумму всех членов потока платежей с начисленными на них процентами к концу срока. Для этого рассмотрим конкретную задачу. Пусть в течение n лет в банк в конце каждого года вносится по R рублей. На взносы начисляются сложные проценты по ставке i% годовых (рис. 3).

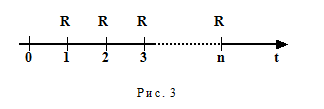
Наращенная сумма S состоит из n слагаемых. Именно

S = R + R( 1 + i ) + R( 1 + i )²+ ...+ R( 1 + i )^n-1

Справа стоит сумма n членов геометрической прогрессии с первым членом R и знаменателем 1 + i. По формуле суммы геометрической прогрессии получим

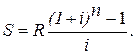(16)

Выражение 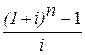обозначается символом s(n;i) и называется коэффициентом наращения обычной ренты. Формулу (16) можно переписать в виде

S = R  s(n; i)

Современной стоимостью ренты A называется сумма всех членов ренты, дисконтированных на начало срока ренты. Из условия эквивалентности для текущего и наращенного значения обычной ренты находим современное значение ренты А:

S = A( 1 + i )ⁿ или A = S( 1 + i )^-n .

Таким образом,

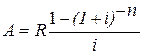. (17)

Выражение 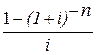обозначается символом a(n;i) и называется дисконтирующим множителем обычной ренты или коэффициентом приведения ренты. Таким образом, современное значение ренты

A = R × a(n; i) .

Пример. Найдите текущее и наращенное значение ренты с выплатами по 320 тыс. руб. в конце каждого месяца в течение двух лет. Проценты начисляются ежемесячно по номинальной ставке 24 % годовых.

Решение. Эффективная ставка за месяц равна 24 %:12 = 2 % Текущее значение вычисляется по формуле (17):

A = 320 = 6052, 4619 тыс. руб.

Наращенное значение вычисляется по формуле (14):

S = 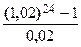= 9734,9952 тыс. руб.

Пример. Фирма приняла решение о создании инвестиционного фонда. С этой целью в течение 5 лет в конце каждого года в банк вносится 100 тыс. руб. под 20 % годовых с последующей их капитализацией, т.е. прибавлением к уже накопленной сумме. Найдите сумму инвестиционного фонда.

Решение. Здесь рассматривается обычная годовая рента с ежегодными платежами R = 100 тыс. руб. в течение n = 5 лет. Процентная ставка i = 20%. Из формулы (16) находим:

S = 100 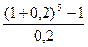= 744,160 тыс. руб.

Приведенная рента

Различие между обычной рентой и приведенной заключается в том, что все выплаты R у приведенной ренты смещены влево на один период относительно выплат обычной ренты (сравним рис. 4а и 4б).

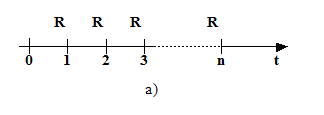
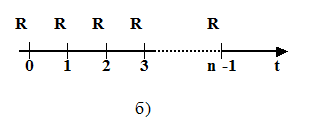
Рис. 4

Легко понять, что на каждый член приведенной ренты начисляется процентов на один период больше, чем в обычной ренте.

Отсюда наращенная сумма приведенной ренты S_P больше в (1 + i ) раз наращенной суммы обычной ренты :

S_P = S (1 + i ) и s^P(n; i) = s(n; i) (1 + i ).

Точно такой же зависимостью связаны современные стоимости обычной ренты А и приведенной ренты А_P :

А_P =А (1 + i ), а^P(n; i) = a(n; i) (1 + i ) . (18)

Пример. Кредит в сумме 5 млн руб. погашается 12 равными ежемесячными выплатами. Процентная ставка по кредиту установлена в размере i=3 % в месяц. Найдите сумму ежемесячного взноса R при платеже:

а) постнумерандо (обычная рента),

б) пренумерандо (приведенная рента).

Решение. а) R × a(12;0,03) = 5 млн руб.

Коэффициент приведения a(12; 0,03) = 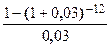= 9,95400 .

Отсюда R = 5млн руб./ 9,95400 = 502311 руб.

б) Аналогично предыдущему : R × a(12;0,03) = 5 млн руб. Из формулы (18):

а^P(12;0,03) = a(12;0,03) × (1+ i ) = 9,954 × 1,03 = 10,25262 ;

R= 5 млн руб./10,25262 = 487680 руб.

Отложенная рента

Если срок ренты начинается в некоторый момент в будущем, то такая рента называется отложеннойили отсроченной. Отложенную ренту будем считать обычной. Длина временного интервала от настоящего момента до начала ренты называется периодомотсрочки. Так период отсрочки ренты с выплатами по полугодиям и первой выплатой через два года равен 1,5 годам (рис. 5).

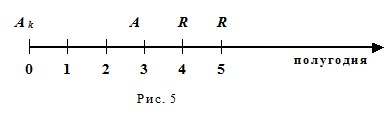
На рис. 5 цифра 3 (1,5 года) означает начало ренты. Начало выплат у отложенной ренты сдвинуто вперед относительно некоторого момента времени. Ясно, что сдвиг по времени никак не отражается на величине наращенной суммы. Иное дело - современная стоимость ренты А.

Пусть рента выплачивается спустя k лет (или периодов) после начального периода времени. На рис.5 начальный период обозначен цифрой 0, а современная стоимость обычной ренты - А. Тогда современная величина отложенной на k лет ренты А_k равна дисконтированной величине А, то есть

А_k = А(1+ i )-k= R·а (n;i) (1+ i )-k. ( 19 )

Пример.Найдите текущее значение отложенной ренты с выплатами по 100 тыс. руб. в конце каждого полугодия, если первая выплата произойдет через два года, а последняя - через пять лет. Проценты начисляются по ставке 20 % за полгода.

Решение. Начало ренты через три полугодия. Первая выплата производится в конце четвертого полугодия, а последняя - в конце. Всего 7 выплат. Из формулы (18) при k = 3; n = 7; i = 0,2 , получим:

А₃ = 100· 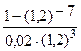= 208599 руб.

Пример.Найдите величину ежегодных выплат отложенной на два года ренты сроком 5 лет, современное значение которой 430 тыс. руб. Проценты начисляются по ставке 21 % годовых.

Решение. Из формулы (19) находим:

R = А_k (1+ i )k/а(n;i)_.

При k = 2; n = 5; i = 0,21 , получим:

R = 430 ·1,21² 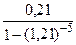= 215163 руб.

Нами был рассмотрен метод расчета наращенной суммы и современной величины, когда выплаты по ренте производятся один раз в году и начисление процентов происходит также один раз в году. Однако в реальных ситуациях (в контрактах) могут предусматриваться и другие условия поступления рентных платежей, а также порядок начисления на них процентов.

5.4. Годовая рента при начисление процентов m раз в году

В этом случае рентные платежи вносятся 1раз в году. Начисление процентов будет производиться по ставке j/m, где j - номинальная (годовая) ставка сложных процентов. Величина наращенной суммы получится из формулы (16) , если в ней положить

i = (1+ j/m)^m - 1 (см. (11)).

В результате получим:

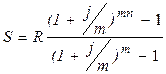(20)

Пример. Страховая компания, заключившая договор с фирмой на 3 года, ежегодные страховые взносы в размере 500 тыс. руб. помещает в банк под 15% годовых с начислением процентов по полугодиям. Определите сумму, полученную страховой компанией по этому контракту.

Решение. Полагая в формуле (20) m = 2; n = 3; R = 500; j = 0,15 , получим:

S = 500 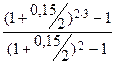= 1 746 500 руб.

5.5. P - срочная рента

Рентные платежи вносятся P раз в году равными суммами, а начисление процентов производится один раз в конце года (m = 1). В этом случае член ренты будет равен R/P, а формула для наращенной суммы получается из формулы (16), в которой ставка за период i_P находится из условия финансовой эквивалентности (всего периодов P·n):

(1 + i ) = (1 + i_P)^P , i _P = (1+ i )^1/P – 1.

Подставляя полученную ставку за период i_P в (16), имеем:

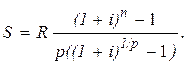(21)

Пример. Страховая компания принимает установленный годовой страховой взнос 500 тыс. руб. дважды в год в течение 3 лет. Банк, обслуживающий страховую компанию, начисляет ей сложные проценты из расчета 15 % годовых один раз в году. Определите сумму, полученную компанией по истечении срока договора.

Решение. Здесь R = 500; n = 3; P = 2; m = 1. По формуле (21) находим:

S = 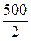· 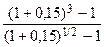= 1779 тыс. руб.

Вечная рента

Под вечной рентой понимается рента с бесконечным числом платежей. Очевидно, что наращенная сумма такой ренты бесконечна, но современная величина такой ренты равна A = R/i. Для доказательства этого факта используем формулу (17) для конечной ренты:

A = R[1-(1+i)^-n]/i.

Переходя в этой формуле к пределу при n ® ¥, получим, что A = R/i.

Пример:Фирма арендует здание за $5 000 в год. Какова выкупная цена здания при годовой ставке процента 10 %?

Решение. Выкупная цена здания есть современная величина всех будущих арендных платежей и равна A = R/i = 50 000 дол.

Объединение и замена рент

Общее правило объединения рент: находятся современные величины рент (слагаемых) и складываются, а затем подбирается рента - сумма с такой современной величиной и нужными остальными параметрами.

Пример. Найдите объединение двух рент: первая длительностью 5 лет с годовым платежом 1000, вторая - 8 и 800. Годовая ставка процента

8 %.

Решение. Современные величины рент равны:

A1 = R1 × a(5;0,08)= 1000 × 3,993 = 3993; A2 = R × a(8;0,08) = =800×5,747=4598.

А = А1 + А2 = 3993 + 4598 = 8591.

Следовательно, у объединенной ренты современная величина А = 8591. Далее можно задать либо длительность объединенной ренты, либо годовой платеж, затем второй из этих параметров определим из формул для рент.

Задачи

5.1.На депозитный счет с начислением сложных процентов по ставке 80 % годовых будут ежегодно в течение 5 лет вноситься суммы по 500 тыс. руб. в начале каждого года. Определите накопленную сумму.

5.2.На депозитный счет в конце каждого квартала будут вноситься суммы по 12,5 тыс. руб., на которые также ежеквартально будут начисляться сложные проценты по номинальной годовой ставке 10 % годовых. Определите накопленную за 20 лет сумму. Ответ: 3 104 783 руб.

5.3.Вычислите сумму, которую необходимо положить на счет частного пенсионного фонда, чтобы он смог выплачивать своим участникам ежемесячно 10 млн. руб. Фонд может инвестировать свои средства по постоянной ставке 5 % в месяц.

(Указание: использовать модель вечной ренты ).

5.4.Бизнесмен арендовал коттедж за $10 000 в год. Какова выкупная цена коттеджа при годовой ставке 5 %. Ответ: $200 000.

5.5.В ходе судебного заседания выяснилось, что г-н А недоплачивал налогов 100 руб. ежемесячно. Налоговая инспекция хочет взыскать недоплаченные за последние два года налоги вместе с процентами (3 % ежемесячно). Какую сумму должен заплатить г-н А.

5.6.Для мелиоративных работ государство перечисляет фермеру $1000 в год. Деньги поступают на специальный счет и на них начисляют каждые полгода 5 % по схеме сложных процентов. Сколько накопится на счете через 5 лет.

5.7.Замените годовую пятилетнюю ренту с годовым платежом $1000 на ренту с полугодовым платежом по $600. Годовая ставка 5 %.

5.8.Замените годовую десятилетнюю ренту с годовым платежом $700 шестилетней годовой рентой. Годовая ставка 8 %.

5.9.Какую сумму необходимо положить в банк родителям студента, обучающегося в платном институте, чтобы раз в полгода в течение 4 лет банк перечислял в институт $420. Банковская ставка 8 % в год.

ПОГАШЕНИЕ ДОЛГА (КРЕДИТА)

В этом параграфе дается применение теории рент к планированию погашения займа (долга).

Разработка плана погашения займа заключается в составлении графика периодических платежей должника. Расходы должника называются расходами по обслуживанию долга или амортизацией займа. Эти расходы включают как текущие процентные платежи, так и средства, предназначенные для погашения основного долга.Существуют различные способы погашения долга. Участники кредитной сделки оговаривают их при заключении контракта. В соответствии с условиями контракта составляется план погашения задолженности. Важнейшим элементом плана является определение числа выплат в течение года, т.е. определение числа срочных уплат и их величины.