Лабораторная работа № 4. Логические функции.

Рассмотрим наиболее часто используемые логические функции ЕСЛИ(), И(), ИЛИ().

Синтаксис функций:

ЕСЛИ(лог_выражение;значение_если_истина;значение_если_ложь)

И(логическое_значение1; логическое_значение2; ...)

ИЛИ(логическое_значение1;логическое_значение2; ...)

Задание 1. Применение логических функций для решения расчетной задачи.

В таблице приведен список деталей, изготовленных рабочим за смену, с указанием общего количества деталей, деталей с браком и себестоимости в рублях одной детали. Рассчитать сумму заработка рабочего за день, зная, что он получит 7% от итоговой суммы за вычетом штрафных удержаний. При расчете учесть, что рабочему начисляется штраф 5% от суммы по каждому виду изделия, если брак по нему составляет 10% и более.

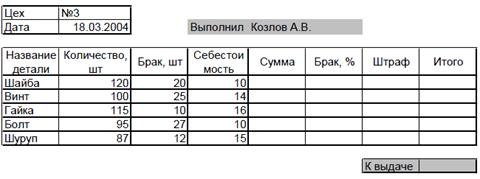
Рис. 10. Исходные данные для задачи

1. Создать таблицу по образцу (рис.10).

2. Подсчитать Сумму по каждому виду изделия (количество*себестоимость).

3. Подсчитать % брака путем деления Брака на Количество и умножения на 100.

4. Используя функцию ЕСЛИ, подсчитать размер штрафа. При этом в пункте «логическое выражение» должно быть сравнение процента брака с 10%. Например, запишем здесь F5>=10 (в ячейке F5 содержится процент брака по шайбам). Тогда в пункте «значение_если_истина» мы должны записать формулу, по которой рассчитывается размер штрафа (т.е. сумма*5/100), а в пункте «значение_если_ложь» напишем 0 (брак в пределах нормы, и штраф в этом случае не будет взыскиваться).

5. Подсчитать итог путем вычитания штрафа из суммы.

6. Подсчитать «К выдаче», просуммировав «Итого» и взяв от этой суммы 7%.

При тех же исходных данных, процент штрафа начисляется иначе. Пусть при проценте брака от 10% до 20% штраф будет по-прежнему 5%, а при проценте брака более 20% штраф будет в размере 12% от суммы. Рассчитать сумму к выдаче при новых условиях.

1. Скопировать основную расчетную таблицу на Лист 2 и затем на Лист 3. Удалить формулы из столбца Штраф.

2. Данную задачу можно решить двумя способами. На Листе 2. реализуем первый способ:

- вызовем функцию ЕСЛИ и в пункте «логическое_выражение» укажем F5<10. Теперь в пункте «значение_если_истина» мы должны указать 0 (штраф не берется, т.к. процент брака менее 10%). А в пункте «значение_если_ложь» необходимо снова вызвать функцию ЕСЛИ (или просто написать от руки ее название прописными буквами русского алфавита без пробелов).

- в новой вызванной функции также нужно заполнить три пункта. «Логическое_выражение» будет проверять на истинность условие, что процент брака более 20% (F5>20). Тогда «значение_если_истина» будет содержать формулу подсчета штрафа в размере 12% от суммы. «Значение_если_ложь» будет содержать формулу подсчета штрафа в размере 5% от суммы.

3. Реализуем второй способ решения задачи с помощью функции И () на Листе 3:

- вызовем функцию ЕСЛИ и в пункте «логическое_выражение» укажем И(F5>=10;F5<20). Здесь будет проверяться на истинность условие, что процент брака составляет более 10% включительно, но менее 20%. Теперь в пункте «значение_если_истина» мы должны указать формулу подсчета штрафа в размере 5% от суммы;

- в пункте «значение_если_ложь» необходимо снова вызвать функцию ЕСЛИ. В новой вызванной функции также нужно заполнить три пункта. «Логическое_выражение» будет проверять на истинность условие, что процент брака более 20% (F5>20). Тогда «значение_если_истина» будет содержать формулу подсчета штрафа в размере 12% от суммы. «Значение_если_ложь» будет содержать в этом случае 0.

Задание 2. Построение графика функции

Рассмотрим пример построения графика функции при 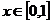с шагом 0,1: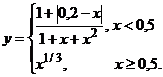

Сначала строится таблица значений, а затем сам график (рис. 11). Здесь мы воспользуемся логической функцией ЕСЛИ. В ячейке B2 формула: =ЕСЛИ(A2<0,5; (1+ABS(0,2-A2))/(1+A2+A2^2); A2^(1/3)). Здесь используется функция ABS для задания модуля разности, она находится в категории «математические».

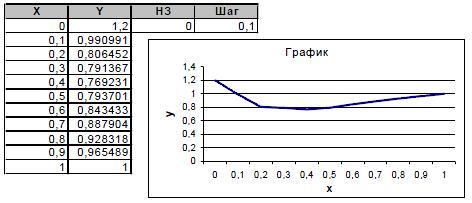
Рис. 11. Построение графика функции с использованием логических функций

Задание 3. Построение поверхности.

Построить поверхность 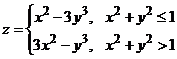при 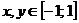, используя функцию ЕСЛИ(). Результат приведен на рис. 12.

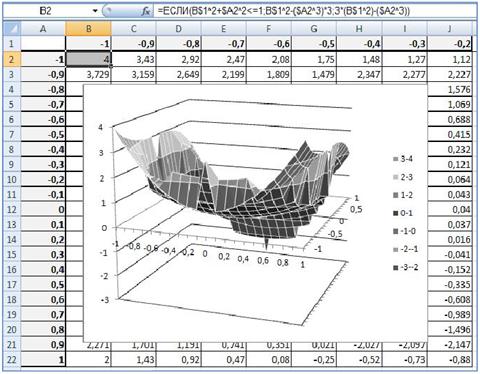
Рис. 12. Результат построения поверхности с использованием логических функций

Используя логические функции и правила построения графиков функций и поверхностей, построить на отдельных листах следующие графики: