Метод плоскопараллельного перемещения

Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 33). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

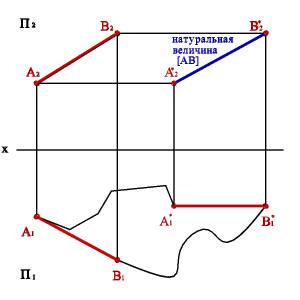
Рис. 33. Определение натуральной величины отрезка методом плоскопараллельного перемещения

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой линии - определяющей траекторию перемещения точек, метод плоскопараллельного проецирования имеет следующие частные случаи:

1. Метод вращения вокруг оси, перпендикулярной плоскости проекций;

2. Метод вращения вокруг оси, параллельной плоскости проекций;

3. Метод вращения вокруг оси, принадлежащей плоскости проекций (вращение вокруг следа плоскости)- способ совмещения.

Рассмотрим некоторые из этих способов.

Метод вращения вокруг оси перпендикулярной

Плоскости проекций

Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 34), выберем ось вращения перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А*1, а точка В не изменит своего положения. Положение точки А*2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А*1. Полученная проекция В2 А*2 определяет действительные размеры самого отрезка.

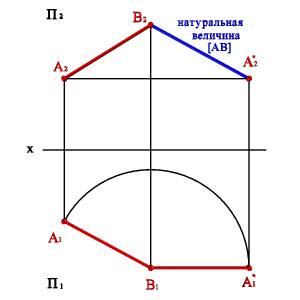
Рис. 34. Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций

Метод вращения вокруг оси параллельной

Плоскости проекций

Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.35). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня - горизонтали. Проведем произвольно фронтальную проекцию горизонтали h2 параллельно оси Ох, которая пересекает прямые в точках А2 и В2 . Определив проекции А1 и В1, построим горизонтальную проекцию горизонтали h1 . Траектория движения всех точек при вращении вокруг горизонтали - окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.

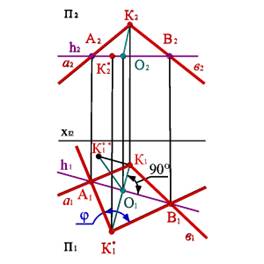
Рис. 35. Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций

Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности - траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО .Продолжим прямую К1О1 так чтобы |КО|=|О1К*1| . Точка К*1 соответствует точке К , когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь - ось вращения. С учетом этого через точку К*1 и точки А1 и В1 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол j - натуральная величина угла между прямыми а и в.