Типы задач начертательной геометрии

Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:

1.Задачи позиционные – решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов (в частном случае, выяснить их взаимную принадлежность) как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.

2.Задачи метрические – при решении задач этой группы появляется возможность ответить на вопросы, касающиеся как внутренней метрики заданных геометрических объектов (определение расстояния между различными точками объекта и нахождения углов между линиями и поверхностями, принадлежащими этому объекту), так и определение расстояний между точками и величин углов между линиями и поверхностями, принадлежащими различным объектам.

В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависит от того, с какими проекциями (удобными или неудобными) приходится иметь дело. При этом наиболее выгодным частным положением геометрического объекта следует считать:

· Положение, перпендикулярное к плоскости проекций (для решения позиционных, а в ряде случаев, и метрических задач);

· Положение, параллельное по отношению к плоскости проекций (при решении метрических задач).

При решении метрических задач, связанных с определением истинных размеров изображенных на эпюре фигур, могут встретиться значительные трудности, если заданные проекции не подвергнуть специальным преобразованиям.

Рассмотрим на примере: Определить расстояние от точки А до прямой m. Расстояние от точки до прямой - это натуральная величина перпендикуляра восстановленного из точки к прямой линии. Простейшим условием такой задачи является случай, когда прямая является проецирующей. Определим расстояние от точки А до прямой m, когда прямая является горизонтально проецирующей линией (рис. 31), т.е. m^П1, m \\ П2, m \\ П3. Согласно, теореме о проецировании прямого угла, перпендикуляр из проекций точки А можно проводить к фронтальной и профильной проекции прямой m, при этом полученный отрезок АК- горизонталь, т.е. параллелен горизонтальной плоскости проекций и на эту плоскость проецируется в натуральную величину.

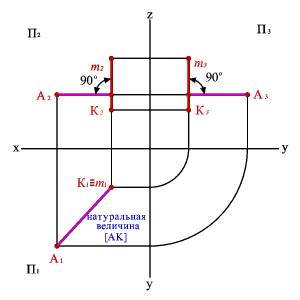
Рис.31. Расстояние от точки до горизонтально проецирующей прямой

Лекция 2

2. Способы преобразования проекций. Характеристика способов. Способ замены плоскостей проекций. Способ вращение. Способ косоугольного вспомогательного проецирования.

Методы преобразования ортогональных проекций

Если прямая параллельна одной из плоскостей проекций т.е. является прямой уровня, то без преобразования ортогональных проекций можно только найти проекции перпендикуляра. Пусть прямая f фронталь, т.е. f \\ П2 значит перпендикуляр можно проводить из проекций А2 к фронтальной проекции прямой m2, на эту плоскость угол будет проецироваться без искажения (рис. 32). Однако полученные проекции отрезка АК не отражают истинной величины отрезка потому, что АК - отрезок прямой общего положения.

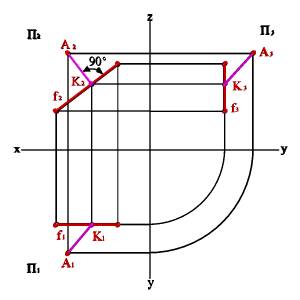
Рис. 32. Расстояние от точки до фронтальной прямой

Общий случай подобной задачи, когда требуется найти расстояние от точки до прямой общего положения, то даже построение проекции искомого отрезка без преобразования проекций не представляется возможным.

Сопоставление приведенных чертежей показывает, что трудности решения одной и той же задачи существенно зависят от положения геометрических объектов относительно плоскостей проекций.

В связи с этим, естественно, возникает вопрос, каким путем можно получить удобные проекции для решения поставленной задачи по заданным неудобным ортогональным проекциям.

Переход от общего положения геометрической фигуры к частному можно осуществлять за счет изменения взаимного положения проецируемой фигуры и плоскостей проекций.

При ортогональном проецировании это достигается двумя путями:

1. Перемещение в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве - метод плоскопараллельного перемещения.

2. Перемещением плоскостей проекций в новое положение по отношению, к которому проецируемая фигура (которая не меняет положения в пространстве) окажется в частном положении - метод замены плоскостей проекций.