Формула начисления сложных процентов

Проценты — удобная относительная мера, позволяющая оперировать с числами в привычном для человека формате не зависимо от размера самих чисел. Это своего рода масштаб, к которому можно привести любое число. Один процент — это одна сотая доля. Само слово процент происходит от латинского «pro centum», что означает «сотая доля».

Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.

Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то сумма вклада с процентами вычисляется по формуле сложных процентов.

S = K * ( 1 + P*d/D/100 )^N

S —суммадепозитаспроцентами,
К —суммадепозита(капитал),
P —годоваяпроцентнаяставка,
N — число периодов начисления процентов.

При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход):

Sp = S - K = K * ( 1 + P*d/D/100 )^N - K

Sp = K * (( 1 + P*d/D/100 )^N - 1)

Пример 1. Принят депозит в сумме 100 тыс. рублей сроком на 90 дней по ставке 20 процентов годовых с начислением процентов каждые 30 дней.

S=100000*(1+20*30/365/100)³=105 013.02
Sp = 100000 * ((1 + 20*30/365/100)^N - 1) = 5 013.02

Еще одна формула сложных процентов.

Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула сложных процентов выглядит так.

S = K * ( 1 + P/100 )^N

S —суммадепозитаспроцентами,
К —суммадепозита(капитал),
P —процентнаяставка,
N — число периодов начисления процентов.

Пример. Принят депозит в сумме 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5 процента в месяц.

S=100000*(1+1.5/100)³=104 567.84
Sp = 100000 * ((1 + 1.5/100)³ - 1) = 4 567.84

Дисконтирование в финансово-экономических рассчетах.

Дисконтирование -

В практике ФЭР может возникнуть и обратная (по отношению к наращению) задача: по известной сумме FV определить объем размещенных средств РV.

Вычисление РУ наоснове FV называется ДИСКОНТИРОВА­НИЕМ.

В этих расчетах величина PV называется приведенной или со­временной стоимостью суммы FV, а при операции наращения сум­ма FV выступает как будущая стоимость величины PV.

Следует иметь в виду, что привести стоимость денег можно к любому нужному моменту времени, не обязательно к началу фи­нансовой операции. Кроме того, с помощью дисконтирования определяют современную стоимость денег независимо от того, действительно ли совершалась кредитная операция и можно ли считать дисконтируемую сумму буквально наращенной.

Прямой расчет FV при ставке i рассмотренный выше (форму­лы (1), (2)), соответствует правилу декурсивных (обычных) про­центов и называется НАРАЩИВАНИЕМ «СО СТА».

Из формул наращивания процентов «со 100» производится обратное действие, или расчет денежных средств, предоставляе­мых в долг (величины PV). Это действие, помимо дисконтирова­ния, называется УЧЕТОМ «НА 100»:

,

.

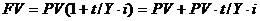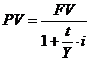Если в формулу (2) вместо PV подставить 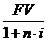, то разница между современной и будущей стоимостью (доход) FV — PV = I составит:

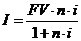, или .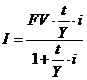

Такой способ начисления дохода называется МАТЕМАТИ­ЧЕСКИМ ДИСКОНТИРОВАНИЕМ, или УЧЕТОМ.

На практике чаще используется так называемый КОММЕР­ЧЕСКИЙ УЧЕТ (БАНКОВСКОЕ ДИСКОНТИРОВАНИЕ) по ставке d, который называется антисипативным (авансовым) расчетом или просто учетом.

Банковский учет дисконтной ценной бумаги заключается для владельца в досрочной ее реализации, а для банка — в приобрете­нии по цене ниже номинала и определении ее стоимости на мо­мент досрочной реализации)

Используя номинал векселя (FV), дисконтную ставку (d), время, оставшееся до срока погашения (t), вычисляют дисконт (Discount — (D)) — скидку с номинала, т.е. разницу между FV и PV:

.

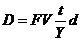Затем рассчитывают выкупную стоимость векселя до срока погашения.

.
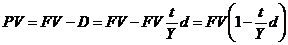