Лекция 5. Задача о беспорядках

Пусть имеется конечное упорядоченное множество элементов {1,…, n}. Из этих элементов могут быть образованы перестановки a₁,…, a_n (a_iÎ{1,…,n}). Число всех возможных перестановок – n!. Среди этих n! перестановок есть такие, что ни один элемент не стоит на своём месте (a_i¹i, i= 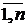). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n-м месте. Такие перестановки называются беспорядками.

Число беспорядков из n элементов обозначается D_n (ясно, что D_n<n!).

Теорема.Число беспорядков из n элементов равно:

.

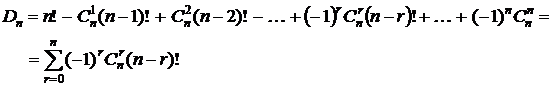# Обозначим через свойство p_i – «i-й элемент стоит на i-м месте». Тогда по формуле решета .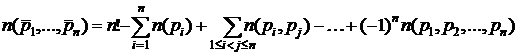

Общее число перестановок n элементов – n! Число перестановок, где i-й элемент стоит на i-м месте, равно (n-1)! (ставим i-й элемент на i-е место, а оставшиеся n-1 элементы переставляем (n-1)! способами). При этом сам i-й элемент можно выбрать 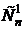способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно .

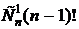Число перестановок, где i-й элемент стоит на i-м месте, а j-й на j-м (i¹j), равно (n-2)!, при этом i-й и j-й элементы можно выбрать 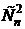способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах – .

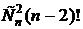Аналогично, число перестановок, где на своих местах стоят хотя бы три элемента – 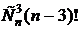. Число перестановок, где на своих местах стоят хотя бы r элементов – 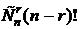. Число перестановок, где все элементы стоят на своих местах 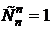. Подставляем в формулу решета: #

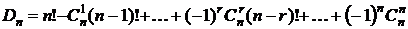Следствие 1.

Так как ,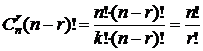

то .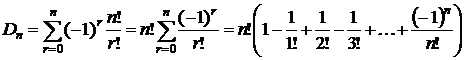

Следствие 2.

Так как 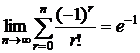, то .

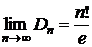Следствие 3.

Рекуррентная формула для числа беспорядков: .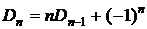

#

#

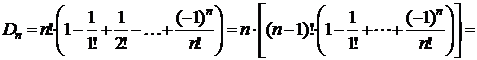
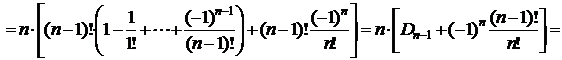
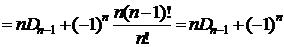Следствие 4.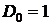

# По рекуррентной формуле из следствия 3 получаем 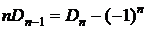или 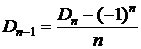. При n=1 получаем 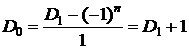. По формуле из следствия 1 получаем 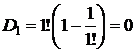. Следовательно, . #

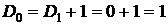Следствие 5.

Ещё одна рекуррентная формула для числа беспорядков: .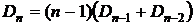

# Рассмотрим n элементов x₁, x₂, … , x_n. Переставим их так, чтобы получить беспорядок. Начнём с x₁: возьмём x₁ и подставим его на место i-го элемента (i¹1). Тогда x_i можно поставить на либо на первое место, либо на какое-то другое, кроме i-го. Если x₁ стоит на i-м месте, а x_i – на 1-ом, то число таких беспорядков – D_n-2 (т.е. число беспорядков оставшихся n-2 элементов). Если x₁ не стоит на первом месте, то такой беспорядок определяется условием:

x₂ не стоит на 2-м месте,

x₃ не стоит на 3-м месте,

…

x_i-1 не стоит на (i-1)-м месте,

x_i не стоит на 1-м месте,

x_i+1 не стоит на (i+1)-м месте,

…

x_n не стоит на n-м месте.

Всего здесь n-1 элемент, то есть число таких беспорядков – D_n-1.

Итак, если x₁ стоит на i-ом месте, то число таких беспорядков D_n-1+D_n-2. Но x₁ можно поставить на любое из (n-1) мест (кроме 1-го). Для каждой установки x₁ справедливы приведённые выше рассуждения.

Таким образом, общее число беспорядков – (n-1)(D_n-1+D_n-2). #

Для проверки полученной формулы вычислим количество беспорядков для некоторых значений n по рекуррентной и прямой формулам. По следствию 4, D₀=1, D₁=0.

Рекуррентная формула	Нерекуррентная формула

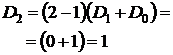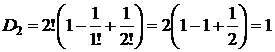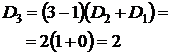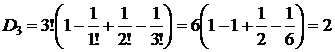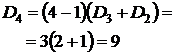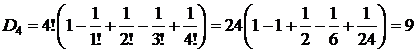Для строгого доказательства правильности рекуррентной формулы, проверим ее в общем виде.

.

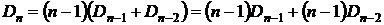Из следствия 3 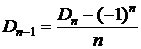, следовательно, 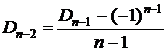. Тогда

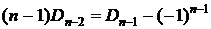. Подставим этот результат в рекуррентную формулу:

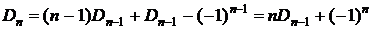. Получили формулу из следствия 3.

Обозначим через D_n,r число перестановок, в которых на своих местах остаются r элементов, а остальные (n-r) образуют беспорядок. Ясно, что D_n,n=1 (все элементы на своих местах), и D_n,0=D_n (ни одного элемента нет на своём месте).

Теорема. .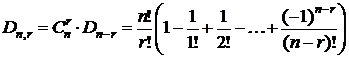

# r элементов, стоящих на своём месте, можно выбрать из n элементов 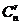способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых D_n-r. Следовательно, всего таких перестановок .

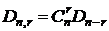С другой стороны, (n-r) элементов, образующих беспорядки, можно выбрать 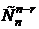способами. Следовательно, 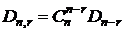. В силу симметричности биномиальных коэффициентов 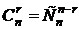, обе формулы дают один и тот же результат.

#

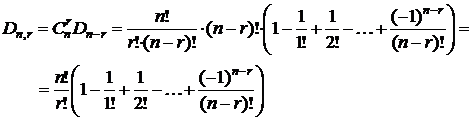Пример.Выстраиваем 5 человек в определённом порядке, после чего 3 из них переставляем так, чтобы они не стояли на своих местах. Сколько таких перестановок?

Ответ: если трое не стоят на своих местах, то оставшиеся двое стоят на своих местах, т.е.

.

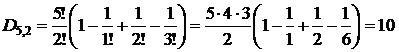Следствие. .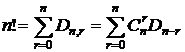

# Из n элементов можно образовать n! перестановок без повторений.

Среди них будет D_n,0 таких, где ни один элемент не стоит на своём месте;

D_n,1 таких, где по одному элементу стоит на своём месте;

D_n,2 таких, где по паре элементов стоит на своих местах;

и т.д.;

D_n,n=1 таких, где все элементы стоят на своих местах.

Следовательно, общее число перестановок (n!) равно сумме этих чисел. #