Проблемы и задачи комбинаторики

Комбинаторика изучает приёмы нахождения числа различных комбинаций, составленных из данных предметов (элементов дискретного множества предметов) при определённых условиях.

Комбинация – некоторое сочетание предметов.

Типы комбинаторных проблем

1. Проблемы существования. Доказывается теоретически, что есть решение или нет.

2. Если решения задачи есть, то сколько их.

3. Выбрать наиболее экономичный способ решения.

Типы комбинаторных задач

1. Задача о маршрутах.

2. Задача о размещении.

3. Задача о покрытии.

4. Задача об укладке.

5. Задача о разбиении.

Все остальные задачи представляют собой объединение, пересечение, произведение указанных типов задач.

Пусть S – множество из n элементов (|S|=n). Говорят, что S – n-множество.

T1 T2   Tn

Задача о покрытии

Найти такие множества T_i, i = 1, 2, …, r, чтобы 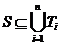(чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков пола быть не должно.

Во многих задачах покрытие должно быть наиболее экономичным (так называемое минимальное покрытие), когда число множеств T_i должно быть минимальным, сами они должны содержать минимально возможное число элементов.

Задача о укладке

Найти такие попарно непересекающиеся множества T_i, i = 1, 2, …, r, (T_i ÇT_j = Æ при i¹j) чтобы 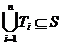(чтобы объединение этих множеств вошло в S). (нарисовать)

Например, уложить несколько предметов в одну коробку. Между предметами могут быть пустые промежутки, но сами предметы друг с другом не пересекаются и укладываются в коробку.

Во многих задачах укладка должна быть наиболее экономичной, когда укладывается максимально возможное количество предметов, а количество пустых промежутков должно быть как можно меньше.

Задача о разбиении

Найти такие попарно непересекающиеся множества T_i, i = 1, 2, …, r, (T_i ÇT_j = Æ при i¹j) чтобы 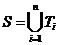(чтобы объединение этих непересекающихся множеств дало S). (нарисовать)

Например, группы в институте – это разбиение множества студентов института. Группы не пересекаются, а их объединение дает множество всех студентов института.

Правила суммы и произведения

Правило суммы

Если объект a можно выбрать p способами, а объект b – другими q способами, то выбор “либо a, либо b” может быть осуществлен p+q способами. При этом выборы a и b являются взаимно исключающими.

Например, в вазе лежит 3 яблока и 5 груш. Тогда взять из вазы либо одно яблоко, либо одну грушу (взаимоисключающие события) можно 3+5 = 8 способами.

Обобщённое правило суммы

Пусть дано r множеств T_i (i=1,…,r), каждое из которых содержит n_i элементов (T_i - n_i‑множество), причём множества взаимно не пересекаются: T_iÇT_j=Æ при i¹j. Тогда объединение этих множеств S=T₁È T₂È…ÈT_r есть (n₁+…+n_r)-множество. .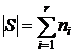

Правило произведения

Если объект a можно выбрать p способами, и после каждого из таких выборов объект b можно выбрать q способами, то выбор “a и b” в указанном порядке может быть осуществлен p·q способами. При этом выборы a и b являются независимыми.

Например, в вазе лежит 3 яблока и 5 груш. Тогда взять из вазы одно яблоко и одну грушу (события происходят совместно) можно 3·5 = 15 способами.