Сортировка вставками (insert)

Сортировка простыми вставками в чем-то похожа на вышеизложенные методы.

Аналогичным образом делаются проходы по части массива, и аналогичным же образом в его начале "вырастает" отсортированная последовательность...

Однако в сортировке пузырьком или выбором можно было четко заявить, что на i-м шаге элементы a[0]...a[i] стоят на правильных местах и никуда более не переместятся. Здесь же подобное утверждение будет более слабым: последовательность a[0]...a[i] упорядочена. При этом по ходу алгоритма в нее будут вставляться (см. название метода) все новые элементы.

Будем разбирать алгоритм, рассматривая его действия на i-м шаге. Как говорилось выше, последовательность к этому моменту разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n].

На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива.
Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним.
В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.

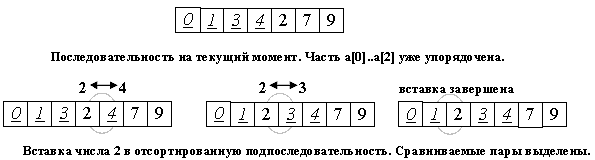
Таким образом, в процессе вставки мы "просеиваем" элемент x к началу массива, останавливаясь в случае, когда

1. Hайден элемент, меньший x или
2. Достигнуто начало последовательности.

template<class T>

void insertSort(T a[], long size) {

T x;

long i, j;

for ( i=0; i < size; i++) { // цикл проходов, i - номер прохода

x = a[i];

// поиск места элемента в готовой последовательности

for ( j=i-1; j>=0 && a[j] > x; j--)

a[j+1] = a[j]; // сдвигаем элемент направо, пока не дошли

// место найдено, вставить элемент

a[j+1] = x;

}

}

Аналогично сортировке выбором, среднее, а также худшее число сравнений и пересылок оцениваются как Theta(n²), дополнительная память при этом не используется.

Хорошим показателем сортировки является весьма естественное поведение: почти отсортированный массив будет досортирован очень быстро. Это, вкупе с устойчивостью алгоритма, делает метод хорошим выбором в соответствующих ситуациях.

Алгоритм можно слегка улучшить. Заметим, что на каждом шаге внутреннего цикла проверяются 2 условия. Можно объединить из в одно, поставив в начало массива специальный сторожевой элемент. Он должен быть заведомо меньше всех остальных элементов массива.

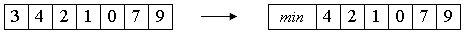
Тогда при j=0 будет заведомо верно a[0] <= x. Цикл остановится на нулевом элементе, что и было целью условия j>=0.

Таким образом, сортировка будет происходить правильным образом, а во внутреннем цикле станет на одно сравнение меньше. С учетом того, что оно производилось Theta(n²) раз, это - реальное преимущество. Однако, отсортированный массив будет не полон, так как из него исчезло первое число. Для окончания сортировки это число следует вернуть назад, а затем вставить в отсортированную последовательность a[1]...a[n].

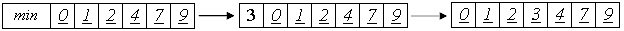
// сортировка вставками со сторожевым элементом

template<class T>

inline void insertSortGuarded(T a[], long size) {

T x;

long i, j;

T backup = a[0]; // сохранить старый первый элемент

setMin(a[0]); // заменить на минимальный

// отсортировать массив

for ( i=1; i < size; i++) {

x = a[i];

for ( j=i-1; a[j] > x; j--)

a[j+1] = a[j];

a[j+1] = x;

}

// вставить backup на правильное место

for ( j=1; j<size && a[j] < backup; j++)

a[j-1] = a[j];

// вставка элемента

a[j-1] = backup;

}

Функция setmin(T& x) должна быть создана пользователем. Она заменяет x на элемент, заведомо меньший(меньший или равный, если говорить точнее) всех элементов массива.

Сортировка Шелла (shell)

Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками.

Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].

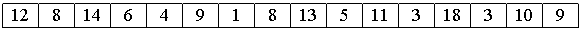
1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).

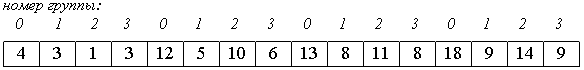
В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.

3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. В конце сортируем вставками все 16 элементов.

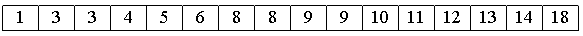
Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные ?

Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.

Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.

Использованный в примере набор ..., 8, 4, 2, 1 - неплохой выбор, особенно, когда количество элементов - степень двойки. Однако гораздо лучший вариант предложил Р.Седжвик. Его последовательность имеет вид

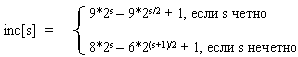
При использовании таких приращений среднее количество операций: O(n^7/6), в худшем случае - порядка O(n^4/3).

Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5, ... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке.
При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.

int increment(long inc[], long size) {

int p1, p2, p3, s;

p1 = p2 = p3 = 1;

s = -1;

do {

if (++s % 2) {

inc[s] = 8*p1 - 6*p2 + 1;

} else {

inc[s] = 9*p1 - 9*p3 + 1;

p2 *= 2;

p3 *= 2;

}

p1 *= 2;

} while(3*inc[s] < size);

return s > 0 ? --s : 0;

}

template<class T>

void shellSort(T a[], long size) {

long inc, i, j, seq[40];

int s;

// вычисление последовательности приращений

s = increment(seq, size);

while (s >= 0) {

// сортировка вставками с инкрементами inc[]

inc = seq[s--];

for (i = inc; i < size; i++) {

T temp = a[i];

for (j = i-inc; (j >= 0) && (a[j] > temp); j -= inc)

a[j+inc] = a[j];

a[j+inc] = temp;

}

}

}

Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s] > size.