Косвенный метод наименьших квадратов

Препятствие к применению метода наименьших квадратов, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если:

1) привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;

2) затем применить метод наименьших квадратов к каждому уравнению в приведенной форме и получить оценки ее параметров;

3) перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров.

Эта методика получила название косвенного метода наименьших квадратов и позволяет получать состоятельные и несмещенные оценки параметров структурной форму системы одновременных уравнений.

Проблема идентификации

Возникает проблема идентификации, то есть однозначности определения параметров структурной модели от приведенной формы. Переход необходим, поскольку экономический смысл и интерпретацию имеют только параметры структурной формы.

Структурный параметр называется идентифицируемым, если он может быть однозначно определен с помощью метода наименьших квадратов. Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры.

Структурный параметр называется неидентифицируемым, если его значение невозможно получить, даже зная точные значения параметров приведенной формы.

Структурный параметр называется сверхидентифицируемым, если косвенный метод наименьших квадратов дает несколько различных его оценок.

Модель:

Для проверки структурной модели на идентификацию, нужно проверить каждое уравнение системы:

1) модель считается идентифицируемой, если каждое уравнение системы идентифицируемо;

2) если хотя бы одно уравнение неидентифицируемо, то вся модель считается неидентифицируемой;

3) если в модели нет неидентифицируемых уравнений, но присутствует хотя бы одно сверхидентифицируемое, то модель – сверидентифицируемая.

Условия идентифицируемости проверяются для каждого уравнения в отдельности. Чтобы уравнение было идентифицируемым, нужно, чтобы:

1+n_x=n_y,

где n_x – число экзогенных переменных, содержащихся в системе, но отсутствующих в данном уравнении системы;

n_y – число эндогенных переменных в данном уравнении.

Если 1+n_x<n_y, уравнение неидентифицируемо;

1+n_x>n_y, то уравнение сверхидентифицируемо.

Оценить параметры можно только для идентифицируемых и сверхидентифицируемых систем. Для однозначно идентифицируемых систем применяется косвенный метод наименьших квадратов. Найти параметры сверхидентифицируемой системы позволяет двухшаговый метод наименьших квадратов.

Использование систем одновременных эконометрических уравнений позволяет строить более реалистичные модели, поскольку отражают взаимосвязи между экономическими переменными. Одна и та же экономическая переменная может рассматриваться и как факторная и как результативная. Использование систем совместных уравнений позволяет решать проблемы, связанные с мультиколлинеарностью факторов в уравнениях множественной регрессии.

При оценке параметров системы одновременных уравнений исследователь сталкивается с проблемой идентификации. Точно идентифицируемые системы могут оцениваться косвенным методом наименьших квадратов.

Наиболее широко системы эконометрических уравнений используются для построения макроэкономических моделей функционирования той или иной страны. Большинство из них представляют собой мультипликаторные модели кейнсианского типа с той ил иной мерой сложности.

Пример: статистическая модель Кейнса для описания народного хозяйства страны в простом варианте имеет следующий вид:

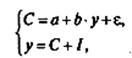
где С – личное потребление в постоянных ценах,

у – национальный доход в постоянных ценах;

I – инвестиции;

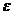- случайная величина.