Нелинейные модели парной и множественной регрессии. Производственные функции

Спецификация модели

Предполагая, что ошибки измерения переменных сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели, то есть ошибкам, вызванным неверным видом уравнения регрессии.

В парной регрессии выбор вида математической функции, моделирующей связь переменных, может быть осуществлен тремя методами:

1) графическим;

2) аналитическим, то есть исходя из теории изучаемой взаимосвязи;

3) экспериментальным.

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих, не учитываемых в уравнении регрессии факторов, тем лучше уравнение регрессии подходит к исходным данным.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в лучшей степени поддаются интерпретации и требуют меньшего объема наблюдений. Число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х.

Классификация нелинейных функций.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Уравнения вида

у = a + 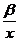4.5.

и у = a х ^b 4.6.

являются нелинейными.

Зависимости (4.5) и (4.6) считаются приемлемыми для описания кривых Энгеля, характеризующих соотношение между спросом на определенный товар (у) и общей суммой дохода (х).

Различают два класса нелинейных регрессий:

1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Примером этого класса моделей могут служить полиномы разных степеней у = а + вх + сх²; у = а + вх + сх²+ dх³, а также равносторонняя гипербола

у = в + а/х.

2) нелинейные регрессии по оцениваемым параметрам:

- степенная у = а х^в

- показательная у = а в^х

- экспоненциальная у = е ^{а+ вх}.

Первый класс моделей (нелинейных по переменным) не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе у = а + вх + сх² , заменяя переменные х₁=х, а х₂=х² , получаем двухфакторное уравнение линейной регрессии у = а + вх₁ + сх₂. Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров.

Для равносторонней гиперболы мы можем заменить 1/х на z и получим линейное уравнение регрессии, оценка параметров которого может быть дана МНК.

Иначе обстоит дело со вторым классом моделей, то есть с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей можно разделить на два типа: а) нелинейные модели внутренне линейные и б) нелинейные модели внутренне нелинейные.

Если модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Пример – степенная функция у = а х^в. Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры а и в неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения приводит его к линейному виду. Соответственно оценки параметров а и в могут быть найдены МНК.

Внутренне нелинейной будет модель вида у = а + вх^с, так как ее невозможно превратить в линейный вид никакими преобразованиями переменных

Возможность построения нелинейных моделей значительно повышает универсальность регрессионного анализа, но и усложняет задачу исследователя – возникает проблема выбора. Выбор модели с максимальным коэффициентом детерминации не всегда возможен. В частности, нельзя сравнивать эти показатели для линейного и логарифмического вариантов модели. В большинстве случаев лучшей следует признать модель, которая при достоверных параметрах имеет меньший объем остаточной вариации, легче интерпретируется и требует меньшего объема наблюдений.

Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.

Факторами производственной функции могут являться следующие переменные:

1) объём выпущенной продукции (в стоимостном или натуральном выражении);

2) объём основного капитала или основных фондов;

3) объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней);

4) затраты электроэнергии;

5) количество станков, потребляемое в производстве и др.

Однофакторные производственные функции (т. е. функции с одной факторной переменной) относятся к наиболее простым производственным функциям. В данном случае результативной переменной является объём производства у, который зависит от единственной факторной переменной х. В качестве факторной переменной может выступать любая из вышеназванных переменных.

Основными разновидностями однофакторных производственных функций являются:

1) линейная однофакторная производственная функция вида:

y=β0+β1x,

например, производственная функция зависимости объёма производимой продукции от величины затрат определённого ресурса. Линейная однофакторная производственная функция характеризуется двумя особенностями:

а) если величина факторной переменной х равна нулю, то объём производства у не будет нулевым, потому что y=β0(β0›0);

б) объём произведённой продукции у неограниченно возрастает при увеличении затрат определённого фактора х на постоянную величину β1 (β1›0). Однако данное свойство линейной однофакторной производственной функции чаще всего справедливо только на практике;

2) параболическая однофакторная производственная функция вида:

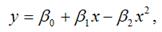
при условиях β0›0, β1›0, β2›0.

Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля;

3) степенная однофакторная производственная функция вида:

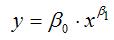
при условиях β0›0, β1›0.

Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений;

4) показательная однофакторная производственная функция вида:

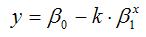
при условиях 0‹β1‹0.

Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0.

5) гиперболическая однофакторная производственная функция вида:

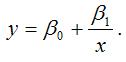
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства.

Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу.

Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x1,x2)=const, называются изоквантами.

Изоквантойназывается сочетание минимально необходимых ресурсных затрат для заданного уровня объёма производства.

Многофакторные производственные функции используются для изучения зависимости объёма производства от n-го количества факторов производства.

Общий вид многофакторной производственной функции:

y=f(xi),

где