Классическая линейная модель множественной регрессии (КЛММР)

в рамках КЛММР рассматриваются только линейные функции регрессии

взаимная некоррелированность случайных регрессионных остатков (E(_i_j) = 0 для i  j). Это требование к регрессионным остаткам ₁,...,_n относится к основным предположениям классической модели и оказывается вполне естественным в широком классе реальных ситуаций, особенно, если речь идет о пространственных выборка, т.е. о ситуациях, когда значения анализируемых переменных регистрируются на различных объектах (индивидуумах, семьях, предприятиях, банках, регионах и т. п.). В этом случае данное предположение означает, что «возмущения» (регрессионные остатки), получающиеся при наблюдении одного какого-либо обследуемого объекта, не влияют на «возмущения», характеризующие наблюдения над другими объектами, и наоборот.

Тот факт, что для всех остатков ₁,₂,...,_n выполняется соотношение E_i²; =², где величина ²от номера наблюдения i не зависит, означает неизменность (постоянство, независимость от того, при каких значениях объясняющих переменных производятся наблюдения) дисперсий регрессионных остатков. Последнее свойство принято называть гомоскедастичностью регрессионных остатков.

ранг матрицы X, составленной из наблюденных значений объясняющих переменных, д-б максимальным, т. е. равнялся бы числу столбцов этой матрицы, которое в свою очередь должно быть меньше числа ее строк (т. е. общего числа имеющихся наблюдений). В дальнейшем нам удобнее будет оперировать с матричной записью модели. При этом кроме обозначений введем также матрицы (векторы):

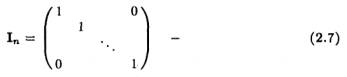
единичная матрица размерности п х п;

вектор-столбец неизвестных значений параметров;

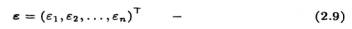
вектор-столбец регрессионных остатков;

вектор-столбец высоты п, состоящий из одних нулей;

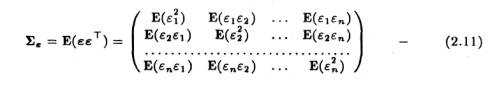
ковариационная матрица размерности п х п вектора остатков;

вектор-столбец оценок неизвестных значений параметров;

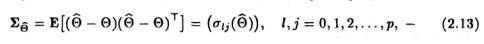
ковариационная матрица размерности (р+1)*(р+1) вектора несмещенных оценок 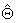неизвестных параметров  (в соотношении _lj() = Е[( 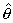_l -_l)( 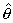_j -_j ))

Тогда матричная форма записи КЛММР имеет вид:

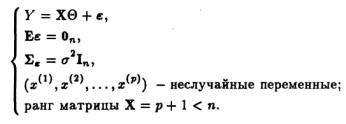
(2.5`)

Когда дополнительно к условиям постулируют нормальный характер распределения регрессионных остатков  = (₁,₂,..., _n)^T(что записывается в виде   N_n (0; ² I_n)), то говорят, что у и X связаны нормальнойКЛММР.

Коренное отличие обобщенной модели от классической состоит только в виде ковариационной квадратной матрицы вектора возмущений: вместо матрицы Σ_ε = σ²E_n для классической модели имеем матрицу Σ_ε = Ω для обобщенной. Обобщенная имеет произвольные значения ковариаций и дисперсий.
Формально обобщенная линейная модель множественной регрессии (ОЛММР) в матричной форме имеет вид:
Y = Xβ + ε (1)
и описывается системой условий:
1. ε – случайный вектор остатков с размерностью n; X -неслучайная матрица значений объясняющих переменных (матрица плана) с размерностью nх(р+1); напомним, что 1-й столбец этой матрицы состоит из единиц;
2. M(ε) = 0_n – математическое ожидание вектора возмущений равно ноль-вектору;
3. Σ_ε = M(εε’) = Ω, где Ω – положительно определенная квадратная матрица; заметим, что произведение векторов ε‘ε дает скаляр, а произведение векторов εε’ дает матрицу размерностью nxn;
4. Ранг матрицы X равен р+1, который меньше n; напомним, что р+1 - число объясняющих переменных в модели (вместе с фиктивной переменной), n - число наблюдений за результирующей и объясняющими переменными.
Следствие 2. Для классической модели ковариационная матрица вектора оценок параметров определялась формулой:
Σ_b = σ²(X’X)^-1 (3)
Эта оценка для обобщенной модели является смещенной (следовательно, и неэффективной).
Следствие 3. Для обобщенной модели ковариационная матрица вектора оценок параметров определяется другой формулой:
Σ _b* = (X’X)^-1X’ΩX(X’X)^-1 (4)

При оценке параметров уравнения регрессии мы применяем метод наименьших квадратов (МНК). В модели у = a + b₁х + b₂ р + е, случайная составляющая (е) представляет собой «необъясненную или ненаблюдаемую величину». После того, как произведено решение модели, то есть дана оценка параметрам, мы можем определить величину остатков в каждом конкретном случае как разность между фактическими и теоретическими значениями результативного признака е_i=y_i- 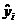. Поскольку это не есть реальные остатки, то мы их считаем лишь выборочной реализацией неизвестного остатка заданного уравнения. При изменении спецификации модели, добавления в нее новых наблюдений, выборочные оценки остатков могут меняться, поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений, то есть остаточных величин.

Выборочные оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют важное практическое значение в использование результатов регрессии и корреляции.

Несмещенные оценки означают, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оценок коэффициента регрессии в найденный параметр по результатам одной выборки можно рассматривать как среднее значение из большого числа несмещенных оценок.

Оценки считаются эффективными, если они характеризуются меньшей дисперсией (то есть мы имеем минимальную вариацию выборочных оценок).

Оценки считаются состоятельными, если их точность увеличивается с увеличением объема выборки.

Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

Предпосылки МНК:

1- случайный характер остатков; Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и МНК оправдан.

2- гомоскедастичность – дисперсия остатков одинакова для всех значений фактора; Если это условие не соблюдается, то имеет место гетероскедастичность.Наличие гомо- или гетероскедастичности можно видеть по графику зависимости остатков от теоретических значений результативного признака.

проводят также ее количественное подтверждение. При малом объеме выборки, что характерно для эконометрических исследований для этих целей используется метод Гольдфельда –Квандта, который включает в себя следующие шаги:

1. Упорядочение наблюдений по мере возрастания фактора х.

2. Исключение из наблюдений нескольких центральных наблюдений (С). При этом должно выполняться условие, что (N – С)/2 должно быть больше р – число параметров в модели.

3. Распределение оставшихся наблюдений на две равные группы с малыми и большими значениями факторного признака.

4. Решение уравнения регрессии для каждой группы (имеем два уравнения).

5. Определение остаточной суммы квадратов отклонений для каждой группы и определение их отношения (отношение большей к меньшей).

6. Сравнение этого отношения с табличным значением критерия Фишера (d f = n - C – 2p/2). Если это отношение меньше табличного значения F- критерия, то мы имеем гомоскедастичные остатки. Чем больше это отношение превышает табличное, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.

3- отсутствие автокорреляции остатков (то есть остатки распределены независимо друг от друга); Автокорреляция – это наличие тесной корреляционной зависимости между остатками текущих и предшествующих наблюдений, если наблюдения упорядочены по фактору х. Автокорреляционная зависимость определяется по линейному коэффициенту корреляции между текущими и предшествующими наблюдениями.

4- остатки подчиняются нормальному закону распределения. Соответствие распределение остатков нормальному закону распределения можно проверить с помощью критерия Пирсона как критерия.

В тех случаях, когда эти предпосылки выполняются, оценки, полученные по МНК, будут обладать вышеназванными свойствами, если же некоторые предпосылки не выполняются, то необходимо корректировать модель.

При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять или исключать некоторые факторы, преобразовывать исходные данные. В частности, при нарушении гомоскедастичности и наличии автокорреляции остатков рекомендуется традиционный МНК, который проводится по исходным данным, заменять обобщенным методом наименьших квадратов, который проводится по преобразованным данным.