Выбор в условиях неопределенности
ВЫБОР В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Неопределенность и риск. Функция ожидаемой полезности.
Денежные лотереи и отношение к риску.
Модель обусловленных благ
Построение деревьев решений.
Для подготовки к лекции необходимо освежить знания по дисциплине и темам:
Теория вероятности
Контрактные отношения – рисколюб, рисконенавистник, контракт как перенесение бремени риска
Определение терминов неопределенности и риска по Норту, Фридмену.
Теория ограниченной рациональности – смысл
Классификация рисков: страновой рисковый коэффициент
Следствие аксиомы независимости.
Если предпочтения, определенные на 
, удовлетворяют аксиоме независимости и лотереи L,L` 
таковы, что L 
L`, α,β ∊ (0,1), то :
αL + (1-α)L` βL + (1-β)L` тогда и только тогда, когда α 
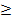β;
αL + (1-α)L`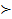 
βL + (1-β)L` тогда и только тогда, когда α > β;
Существование функции ожидаемой полезности
Функция полезности фон Неймана-Моргенштерна может подвергаться лишь монотонным преобразованиям вида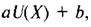 
при a>0 , т.е. аффинным преобразованиям[1], изменяющим исходную точку и/или масштаб вертикальной оси, но не влияющим на «форму» функции. Поэтому данная функция является кардиналистской: ее нельзя считать лишь неким индексом полезности — ее конкретные значения имеют вполне определенный смысл. Соответственно, конкретный смысл приобретают и рассуждения о возрастающей, неизменной и убывающей предельных полезностях.
Модель обусловленных благ
Обусловленными благамибудем называть блага, доступ к которым для индивида обусловлен наступлением одного или другого из указанных исходов, имеющим место с заданной вероятностью
Выбор в мире двух таких благ формально можно свести к решению уже известной нам задачи максимизации полезности, получаемой индивидом, при заданном бюджетном ограничении. Правда, теперь, в отличие от выбора при определенности, в конечном итоге индивид получит лишь одно из обусловленных благ (какое именно из двух, будет зависеть от того, наступит хороший исход или же плохой). Однако пока неопределенность не будет разрешена, индивид вынужден осуществлять выбор из обоих обусловленных благ и, возможно, купит сколько-нибудь каждого из них, поскольку не знает, какой именно из исходов будет иметь место.
Пусть возможно S состояний мира (состояний природы), определяемых состоянием экзогенных факторов. В общем виде, s = 1, … , S. Назовем контингентным благом[2] xij право (контракт) на получение i-го физического блага в количестве xij в случае реализации состояния s.
Формально выбор в мире двух таких благ можно свести к решению уже известной задачи максимизации полезности. Предположим, в частности, что завтра мир будет находиться лишь в одном из двух возможных состояний: «хорошего» исхода событий или «плохого»: Wg — богатства «при хорошем исходе» Wb — богатства «при плохом исходе». Ожидаемая полезность потребления обусловленных благ (двух разных уровней богатства) есть:
Кривая безразличия при таком выборе есть геометрическое место комбинаций обусловленных благ, имеющих одинаковый уровень ожидаемой полезности ( 
) для потребителя.
 |  |  |
| . а) предпочтения «рисконейтрала» | . б) предпочтения «рисконенавистника» | . в) предпочтения любителя риска |
На осях отложены количества обусловленных благ: Wg - богатства «при хорошем исходе» — по горизонтальной оси и Wb — богатства «при плохом исходе» — по вертикальной оси. Норма замещения, как обычно, показывает пропорцию, в которой индивид готов заместить товар, количество которого отложено по вертикальной оси (в данном случае богатство «при плохом исходе»), товаром, количество которого отложено по горизонтальной оси (богатством «при хорошем исходе»). Как нам известно, норма замещения есть отношение предельных полезностей, или, при функции полезности.
Для «рисконейтрала» предельная норма замещения есть также величина постоянная и равная отношению вероятностей 
Для индивида, не склонного к риску, предельная полезность богатства убывает с ростом богатства и растет с его уменьшением. Поэтому при движении вдоль кривой безразличия в направлении увеличения Wg и уменьшения Wb предельная норма замещения должна падать, т.е. кривая безразличия будет выпуклой к началу координат.
Предположим, что исходный уровень богатства индивида, доступный ему гарантированно, вне зависимости от того, хорошие наступят времена или плохие, составляет W*, тогда луч образованный всеми точками Wb = Wg (биссектриса) называется«линией уверенности»
Линия CC` - линией ожидаемой стоимости и представляет все варианты выбора (или игр) с одинаковой ожидаемой стоимостью, равной исходному богатству индивида, однако все они, за исключением варианта, отображенного точкой А (на: пример, варианты, показанные точками D и В), являются рисковыми.
Предположим, что индивид рискнет поставить на кон часть богатства W* и выиграет Wg в размере G, т.е. переместится из точки А по направлению к точке В. Это будет означать изменение в структуре его богатства в пользу Wg, при отказе от части Wb в размере L. Он мог бы поставить на кон все исходное богатство W* и, выиграв, тем самым полностью обменять богатство при плохом исходе на богатство при хорошем исходе. Пропорция этого обмена задана отношением вероятности исхода по горизонтальной оси к вероятности исхода по вертикальной оси. Этот выигрыш может рассматриваться как продажа товара «рубли в плохие времена» и покупка товара «рубли в хорошие времена» по соответствующим рыночным ценам Рb и Pg, причем 
Проиграв, т.е. идя от точки А в обратном направлении к точке D и далее, он совершил бы по этим же ценам обмен обратного рода.
Линия ожидаемой стоимости аналогична бюджетной линии индивида с доходом W* и наклоном, равным отношению вероятностей 
отображающим относительную цену 
поскольку сами цены условных благ равны соответствующим вероятностям: Pg = Р, Рь = 1 — р.
Это равенство цен вероятностям характеризует обмен обусловленных благ индивидом как актуарно справедливую игру, или игру со справедливыми шансами, что верно для развитых рынков этих благ, когда в обществе имеется согласие относительно численного значения вероятности наступления «хороших времен» (по аналогии со ставками на бегах: эти ставки «справедливы», если они отражают реальные вероятности выигрыша конкретных лошадей).
? на семинаре разберем модель спроса на страховку, модель уклонения от налогов.
Итак, страхование — это просто рыночный механизм объединения рисков, потенциально ценный для не склонных к риску индивидов. Другая сторона данного явления — так называемое рассредоточение риска. Оно может осуществляться посредством создания специальных институтов — скажем, синдикатов, держатели акций которых совместно владеют каким-то специфическим рисковым активом. В свое время создавались совместные компании, спонсировавшие высокорискованные проекты — путешествия (например, знаменитого пирата сэра Фрэнсиса Дрейка) с целью совершения географических открытий (и/или грабежей). Акционерное финансирование есть способ рассредоточение риска, который несет фирма, между держателями ее акций. В эпоху бурного развития научно-технического прогресса создание совместных компаний и, в частности, компаний по управлению совместными фондами рискового финансирования, стало важным инструментом осуществления инвестиций в разработки и внедрение наукоемких технологий и продукции.
Построение деревьев решений
Зачастую выбор в условиях неопределенности сопряжен более чем с двумя возможными исходами, и в этом случае удобнее сипользовать технику построения деревьев решений,— это схематические отображения задачи выбора, показывающие возможные исходы и их связь с текущими действиями индивида. Деревья включают в себя ветви, а также узлы трех типов:
1) Узел решения (обозначаемый в приведенных ниже схемах кубиком) — точка дерева решений, в которой индивид сталкивается с необходимостью принятия решения, и исходящие из нее ветви представляют доступные ему варианты выбора.
2)Узел случая (обозначаемый в приведенных ниже схемах кружком) — точка дерева решений, движение из которой по исходящим ветвям обусловлено случайным процессом.
3) Конечный узел — это точка, представляющая конечный исход, связываемый с данной конкретной ветвью дерева решений.
Пример. Молодой и перспективный менеджер Николай Александрович в целях карьерного роста намерен пройти обучение по программе МВА. Функция полезности дохода для Николая Александровича имеет вид U = 
, где W— его доход в долларах. Специализируясь в области финансового менеджмента, он может играть на бирже, причем с вероятностью 0,4 будет играть на повышение, что принесет ему 80 000 долл. годового дохода. Если, однако, ему придется играть на понижение, вероятность чего равна 0,6, его годовой доход составит всего 45 000 долл.
Специализируясь в области общего менеджмента, он мог бы с вероятностью 0,2 стать партнером своей компании и получать 120 000 долл. годового дохода. Однако, если ему не удастся стать партнером компании, его годовой доход составит лишь 45 000 долл. Какой вариант специализации ему следует выбрать?
Теорема Эрроу-Пратта
Пусть предпочтения потребителей 1 и 2 представимы функциями ожидаемой полезности с возрастающими, строго вогнутыми дважды непрерывно дифференцируемыми элементарными функциями полезности. Тогда следующие утверждения эквивалентны:
1) rA1 (x) < rA2 (x)
2) u2(x) =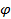 
(u1(x)), где 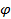– возрастающая, строго вогнутая функция
3) c2(F) < c1(F), для любой лотереи F
Будем говорить, что функция u() демонстрирует убывание абсолютной несклонности к риску, если является убывающей функцией х.
ВЫБОР В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ