ЛАБОРАТОРНАЯ РАБОТА № 7. РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ СРЕДСТВАМИ MS EXCEL
Процесс изменения значений ячеек и анализа влияния этих изменений на результат вычисления формул в Excel называется анализом«что-если».
В данной работе рассматривается процесс нахождения исходных данных, которые при подстановке в формулы, дают необходимое значение в ячейке ре-зультата. Если вы знаете, каким должен быть результат вычисления по форму-ле, то Excel подскажет вам значения одного или нескольких входных парамет-ров, которые позволяют получить нужный результат.
Другими словами, вы можете задать вопрос типа: Какой рост продаж не-обходим для получения дохода в $ 1 200 000? В Excel для этого предусмотрены два подходящих средства.
1. Подбор параметра –определяет значение одной входной ячейки,котороетребуется для получения желаемого результата в зависимой ячейке (ячейке результата).
2.Поиск решения –определяет значения в нескольких входных ячейках,ко-торые требуются для получения желаемого результата. Более того, можно накладывать ограничения на входные данные, поэтому здесь можно по-лучить решение (если оно существует) многих практических задач.
В данной работе рассмотрены обе процедуры.
Подбор параметра
Подбор параметра является удобным средством для решения задач, кото-рые имеют точное целевое значение, зависящее от одного неизвестного пара-метра. С помощью Подбора параметра можно определить значение, которое будет давать желаемый результат.
Решите задачу
Вы хотите положить деньги в банк под 4,5 % и получить ровно 1 000 тг.по истечении года. Необходимо определить сумму вклада. Для решения данной задачи используем средство Подбор параметра.
Задание 1
1. Запустите Excel.
2. Переименуйте первый лист в Подбор параметра.
3. Оформите таблицу (рис. 46). Введите указанную формулу.
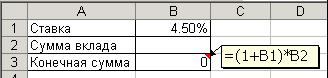
Рис. 46. Исходные данные для подбора параметра
4. Перейдите в ячейку В3. Выполните команду Сервис ⇒ Подбор параметра.
5. В открывшемся диалоговом окне укажите значение необходимой конеч-ной суммы и ссылку на ячейку с искомым значением вклада (рис. 47).
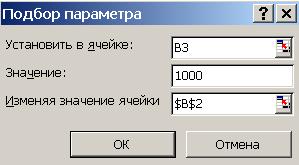
Рис. 47. Диалоговое окно «Подбор параметра»
6. Нажмите кнопку ОК. Средство Подбор параметра найдет решение и со-общит об этом (рис. 48). Нажмите кнопку ОК и убедитесь, что искомое значение помещено в ячейке В2.
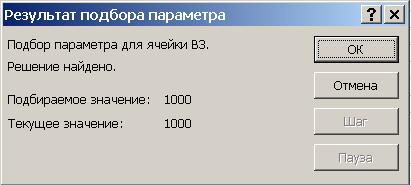
Рис. 48. Диалоговое окно «Результат подбора параметра»
7. Сохраните файл и продемонстрируйте результат преподавателю.
Поиск решения
Задачи, выполняемые с использованием процедуры поиска решения, отно-сятся к сравнительно узкой области. Такие задачи называют оптимизационными. Обычно они затрагивают случаи, удовлетворяющие следующим условиям:
1. Значение в целевой ячейке зависит от других ячеек и формул. Нужно оп-ределить все исходные параметры, при которых значение в целевой ячей-ке будет максимальным, минимальным или заранее определенным.
2. Целевая ячейка зависит от группы ячеек, которые называются изменяе-мыми ячейками.Их значения надо подобрать так,чтобы получить же-лаемый результат в целевой ячейке.
3. Решение (значения изменяемых ячеек) должно находиться в определен-ных пределах или удовлетворять определенным ограничениям.
После соответствующей подготовки рабочего листа можно использовать процедуру поиска решения для подбора значений в изменяемых ячейках и по-лучения в целевой ячейке нужного результата, который одновременно удовле-творяет все установленным ограничениям.
Примечание: если в меню Сервис не отображается команда Поиск решения,выполните команду Сервис ⇒ Надстройки и в диалоговом окне Надстройки установите доступность данной надстройки.
Решите задачу
Фирма производит две модели А и В сборных книжных полок. Их произ-водство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м2 досок, для изделия модели В – 4 м2. Фирма может получать от своих поставщиков до 1700 м2 досок в неделю.
Для каждого изделия модели А требуется 12 мин. машинного времени, для изделия модели В – 30 мин. В неделю можно использовать 160 ч машинно-го времени.
Сколько изделий какой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2 доллара прибыли, каждое изделие В – 4 доллара прибыли?
Задание 2
1. Переименуйте второй лист в Поиск решения, создайте на нем таблицу согласно рис. 49.
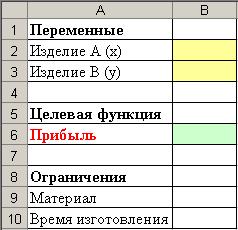
Рис. 49. Исходные данные для задачи на поиск решения
2. Для решения задачи введем две переменные:
− X –количество изделий модели А;
− Y –количество изделий модели В.
3. Ячейки, содержащие переменные, будут являться изменяемыми, т.к. от них будет зависеть результат в целевой ячейке. Присвойте ячейкам В2 и В3 соответственно имена Х и Y. Для этого активизируйте ячейку В2 и вы-полните команду Вставка ⇒ Имя ⇒ Присвоить. В поле Имя введите но-вое имя для ячейки В2: Х. Нажмите кнопку ОК. Аналогичным способом присвойте ячейке В3 имя Y.
Целевой функцией будет являться выражение: 2 · X + 4 · Y. В ячейку В6 введите формулу для вычисления прибыли (рис. 50).
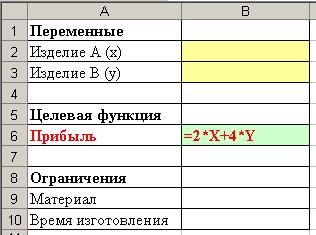
Рис. 50. Формула для расчета прибыли
Но у нас присутствуют ограничения, описанные в условии задачи:
− ограничение количества материала для полок в неделю:
| 3 · X + 4 · Y ≤ 1700, | (6) |
| − ограничение количества машинного времени в неделю: | |
| (12 / 60) · X + (30 / 60) · Y ≤ 160 ⇒ 0,2 · X+0,5 · Y ≤ 160. | (7) |
| 4.Введите формулы ограничений в ячейку В9: | |
| =3 · X + 4 · Y. | (8) |
| В ячейку В10: | |
| =0,2 · X + 0,5 · Y (рис. 51). | (9) |
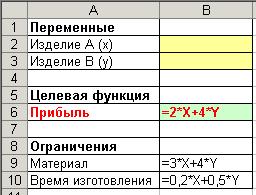
Рис. 51. Формулы для расчета материала и времени изготовления
Необходимо учесть, что количество изделий – неотрицательное число,
поэтому добавляются еще два ограничения: X ≥ 0 и Y ≥ 0.
Количества изделий должны быть целыми числами: X - целое и Y - целое.
5. Установите курсор в ячейку целевой функции В6.
6. Выполните команду Сервис ⇒ Поиск решения.
7. В окне Поиск решения проверьте, чтобы в поле Установить целевую ячейку стояла ссылка на ячейку с целевой функцией (рис. 52).
Рис. 52. Диалоговое окно «Поиск решения: установление целевой ячейки»
8. В поле Равной установите переключатель Максимальному (если в усло-виях задачи будет задано «минимизировать затраты», то необходимо бу-дет переключить в Минимальному, если же будет определено конкретное значение, то выбираем значение и указываем это число) значению (рис. 53).
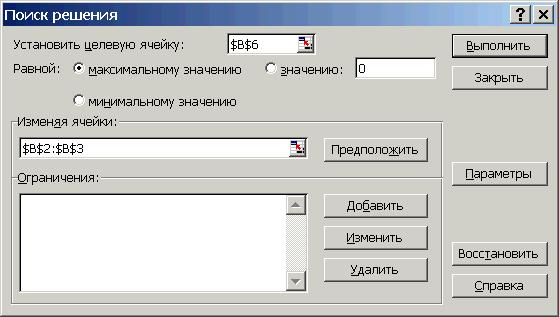
Рис. 53. Диалоговое окно Поиск решения: установление изменяемых ячеек
9. В поле Изменения ячейки укажите диапазон изменяемых ячеек (это те ячейки в которых фиксируется количество выпускаемой продукции) (см. рис. 52).
10. В поле Ограничения задайте ограничения. Для этого нажмите кнопку До-бавить,расположенную рядом с данным полем.
11. В появившемся диалоговом окне Добавление ограничения в поле Ссылка на ячейку укажите ячейку с функцией ограничения материала, в следую-
щем поле из списка выберите оператор ≤ и в поле Ограничение введите число 1700 (рис. 54). Нажмите кнопку Добавить.
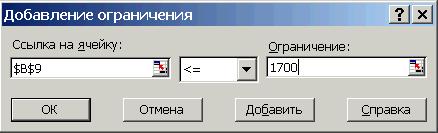
Рис. 54. Диалоговое окно «Добавление ограничения»
12. Таким же образом введите оставшиеся три ограничения и нажмите кноп-ку ОК.
13. Проверьте правильность ввода данных в окне Поиск решения (рис. 55) и нажмите кнопку Выполнить.
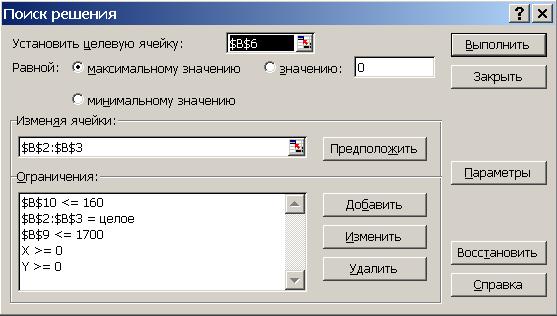
Рис. 55. Диалоговое окно «Поиск решения»
14. В появившемся окне Результаты поиска решения выберите переключа-тель Сохранить найденное решение (рис. 56).
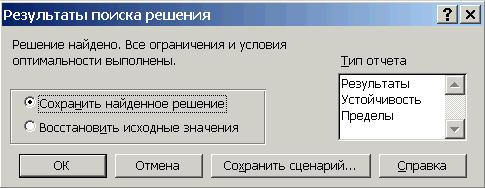
Рис. 56. Диалоговое окно «Результаты поиска решения»
15. В изменяемых ячейках появятся значения, являющиеся оптимальными для поставленных условий, в ячейке с целевой функцией отобразится наибольшее значение прибыли (рис. 57).
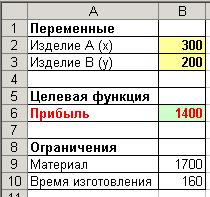
Рис. 57. Результаты решения задачи на поиск решения
16. Сохраните файл и продемонстрируйте результат преподавателю.
Создание сценариев
При решении оптимизационных задач часто возникает необходимость сохранить варианты решения, имеющие множество исходных данных, причем необходимо четко представлять, как изменения исходных данных первых влияют на результат. Ощутимую помощь в анализе такого рода задач могут оказать сценарии Excel.
Сценарий Excel – это инструмент, позволяющий моделировать различные физические, экономические, математические и другие задачи. Он представляет собой зафиксированный в памяти компьютера набор значений ячеек рабочего листа. Используя сценарии, можно сохранить в памяти компьютера несколько наборов исходных данных так, чтобы их можно было быстро загрузить (и по-лучить результат, соответствующий этому набору исходных данных).
Таким образом, создав сценарий, пользователь получает возможность уз-нать, что произойдет с результатом, если поменять исходные значения в неко-торых ячейках листа. Кроме того, в случае необходимости всегда можно вер-нуться к одному из вариантов, рассмотренных ранее.
Сценарии Excel можно использовать не только при работе с решениями оптимизационных задач. Сценарии очень удобны при решении задач подбора параметров и вообще в тех случаях, когда необходимо зафиксировать несколь-ко различных наборов исходных данных, содержащих большое количество.
Задание 3
1. Для раннее выполненной задачи (на рабочем листе Поиск решения) за-пустите вновь Поиск решения.
2. В появившемся окне Результаты поиска решения (рис. 58) нажмите на кнопку Сохранить сценарий...
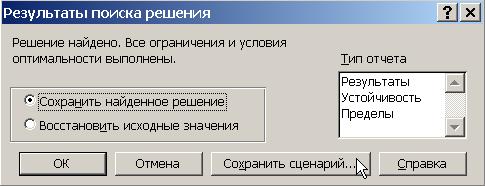
Рис. 58. Диалоговое окно «Результаты поиска решения»
3. В новом окне задайте имя сценария Материал_1700 (рис. 59). Нажмите кнопку ОК. Далее закончите процедуру Поиска решения.
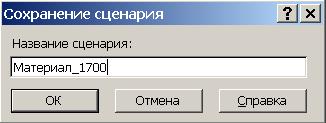
Рис. 59. Диалоговое окно «Сохранение сценария»
4. Снова запустите решение задачи. Измените ограничение на расход мате-риала (рис. 60).
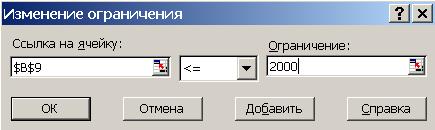
Рис. 60. Диалоговое окно «Изменение ограничения»
5. Выполните поиск решения и сохраните решение в сценарии под именем Материал_2000.
6. Выполните команду Сервис ⇒ Сценарии...
7. В открывшемся Диспетчере сценариев выделите сценарий в нажмите на кнопку Вывести (рис. 61).
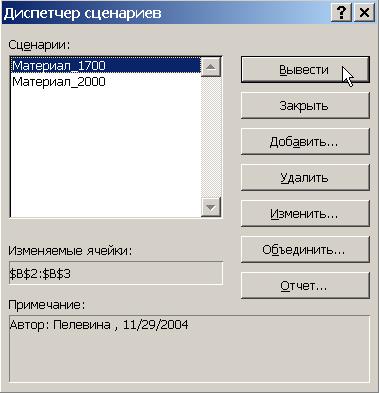
Рис. 61. Диалоговое окно «Диспетчер сценариев»
8. Убедитесь, что значения в ячейках таблицы изменились в соответствии со сценарием.
9. Сохраните файл и продемонстрируйте результат преподавателю.
Создание таблиц подстановки
При работе с моделью «что, если» в определенный момент времени мож-но использовать только один сценарий (только один набор исходных данных). Возникают случаи, когда необходимо сравнить результаты нескольких сцена-риев. Для этого используются так называемые таблицы подстановки.
Таблицы подстановки позволяют производить вычисления по формулам, для одного из нижеприведенных случаев:
− имеется один набор данных для одной ячейки (одной переменной), на ко-торую ссылаются несколько формул. В этом случае создается так назы-ваемая таблица подстановки с одним входом;
− имеются два набора данных для двух ячеек (две переменные), на которые ссылается одна формула. Создаваемая в этом случае таблица называется таблицей подстановки с двумя входами.
