Аргументы для анализа инвестиций

Аргумент	Название	Описание
Пс	Приведенная стоимость(начальная)	Общая сумма, которая на настоящий момент равноценна ряду будущих выплат.
Бс	Будущая стоимость инвестиции	Сумма, которая будет достигнута после последней выплаты.
Плт	Выплата	Сумма, выплачиваемая в каждый период и не меняющаяся за все время выплаты инвестиции.
Кпер	Общее число периодов выплаты инвестиции-	Рассчитывается как произведение количества лет инвестиции на количество выплат в год. Например, кредит выдан на 5 лет с выплатой 2 раза в год. Число периодов равно 5 · 2 = 10.
Ставка	Процентная ставка за период	Рассчитывается как процентная ставка за год, деленная на количество выплат в год. Например кредит выдан под 10 % годовых с ежеквартальны ми выплатами. Процентная ставка за период равна 10 / 4=2,5 %.
Тип	Вид аннуитета (тип)	Принимает логическое значение 0 или 1. Значение0 обозначает, что выплата производится в конце периода, 1 – в начале периода.

Финансовые функции связаны с интервалами выплат. Аннуитет – это ряд постоянных денежных выплат, делаемых в течение длительного периода. Например, заем под автомобиль или заклад являются аннуитетами.

В функциях, связанных с аннуитетами, выплачиваемые денежные средст-ва, такие как депозит на сбережения, представляются отрицательным числом; полученные денежные средства, такие как чеки на дивиденды, представляются положительным числом.

Например, депозит в банк на сумму 1000 тг.представляется аргументом –1000 – для вкладчика – и аргументом 1000 – для банка.

3.1. Расчет текущей стоимости инвестиции. Функция ПС (ПЗ)

Функция ПС (приведенная стоимость) является одним из наиболее рас-пространенных способов оценки привлекательности долговременных вложе-ний. Текущее значение вложения (чистый текущий объем вклада) определяется дисконтированием (приведением к стоимости на настоящий момент) поступле-ний по этому вложению. Если текущая стоимость поступлений оказывается больше вклада, вложение считается удачным.

Синтаксис функции: ПС(Ставка;Кпер;Плт;Бс;Тип).

Функция ПС вычисляет текущую стоимость ряда равных по величине пе-риодических выплат или единовременной выплаты.

Для вычисления текущей стоимости ряда выплат используется аргумент

Плт (выплата).

Для вычисления текущей стоимости единовременной выплаты используется аргумент Бс (будущая стоимость).

Для вложения с рядом периодических выплат и единовременной выплаты используются оба эти аргумента.

Задание 1

Определение текущей стоимости ряда периодических выплат. Существу-ет два варианта вложения денежных средств с целью заработать 5 000 тг.в те-чение 2,5 лет:

1. Совершить сделку, которая каждые полгода возвращает 1 000 тг.в тече-ние следующих 2,5 лет. Для этого нужно вложить 4 000р.

2. Вложить деньги в банк на краткосрочный счет под 8,0 % с выплатами ка-ждые полгода в размере 1 000 тг.

Определить, какой из вариантов вложения денежных средств является более выгодным.

Пояснения к задаче

Решение этой задачи требует оценить текущую стоимость ряда поступле-ний по 1 000 тг.Проценты, которые предлагает банк, послужат в качестве учетной ставки вложения. Учетная ставка является своего рода «барьером», ко-торый должен быть превзойден, прежде чем инвестиция станет привлекатель-ной, поэтому ее часто называют барьерной ставкой.

Для определения текущей стоимости вложения используется функция ПС, в которой будет задействован аргумент Плт и не задействован аргумент Бс.

Ход решения задачи

1. Запустите Excel.

2. Переименуйте первый лист в ПС.

3. Оформите таблицу согласно (рис. 17).

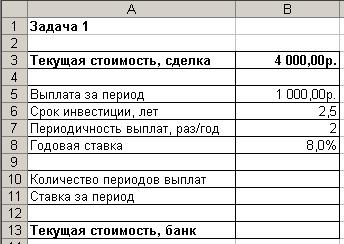
Рис. 17. Исходные данные для расчета текущей стоимости ряда периодических выплат

4. Вычислите количество периодов выплат и ставку за период согласно рис. 18).

5. Запустите Мастер функций, ознакомьтесь с функцией ПС (ПЗ).

6. Вычислите текущую стоимость инвестиции. Результаты сравните с рис. 18.

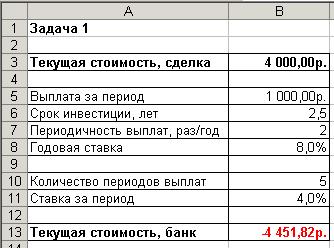
Рис. 18. Результаты вычисления текущей стоимости ряда периодических выплат

7. Сохраните файл и продемонстрируйте результат преподавателю.

Анализ результатов решения

Функция возвращает значение –4 451,82. Это означает, что нужно вложить в банк 4 451,82 тг.под 8,0 % годовых сегодня, чтобы получить 5 000 тг.в течение следующих 5 лет. Поскольку в предлагаемой сделке вклад равен 4 000 тг., можно считать, что совершить сделку выгоднее, чем вложить деньги в банк.

Задание 2 Определение текущей стоимости диновременной выплаты

Существует два варианта вложения денежных средств с целью получения

5 000 тг.по истечению 2,5 лет:

1. Совершить сделку, вложив 4 000 тг.

2. Вложить деньги в банк на краткосрочный счет под 8,0 % с начислением процентов каждые полгода.

Определить, какой из вариантов вложения денежных средств является более выгодным.

Пояснения к задаче

Решение этой задачи требует оценить текущую стоимость единовремен-ной выплаты. Для определения текущей стоимости вложения используется

функция ПС, в которой будет задействован аргумент Бс и не задействован ар-гумент Плт.

Ход решения задачи

1. Запустите Excel.

2. Переименуйте первый лист в ПС.

3. Оформите таблицу согласно (рис. 19).

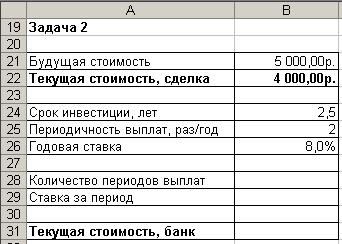
Рис. 19. Исходные данные для расчета текущей стоимости единовременной выплаты

4. Вычислите количество периодов выплат и ставку за период (рис. 20).

5. Вычислите текущую стоимость инвестиции. Результаты сравните с рис. 20.

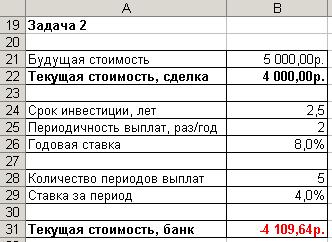
Рис. 20. Результаты вычисления текущей стоимости единовременной выплаты

6. Сохраните файл и продемонстрируйте результат преподавателю.

Анализ результатов решения.

Функция возвращает значение –4 109,64. Это означает, что нужно вло-жить в банк 4 109,64р. под 8,0% годовых сегодня, чтобы получить 5 000 тг.через 5 лет. Поскольку значение 4 109,64 тг.больше, чем текущая стоимость сделки (4 000 тг.), вложить деньги в сделку более выгодно, чем в банк.

Задание 3 Определение текущей стоимости ряда платежей и единовременной выплаты

Существует два варианта вложения денежных средств сроком на 2,5 года.

1. Совершить сделку, которая ежегодно возвращает 500 тг.в течение сле-дующих 2,5 лет. Кроме того, в конце периода будет выплачено 3 000 тг.

2. Вложить деньги в банк на краткосрочный счет под 8,0 % с начислением процентов каждые полгода.

Определить, какой из вариантов вложения денежных средств является более выгодным.

Пояснения к задаче

Решение этой задачи требует оценить текущую стоимость ряда платежей и единовременной выплаты. Для определения текущей стоимости вложения используется функция ПС, в которой будут одновременно задействованы аргу-менты Бс и Плт.

Ход решения задачи

1. Запустите Excel.

2. Переименуйте первый лист в ПС.

3. Оформите таблицу согласно (рис. 21).

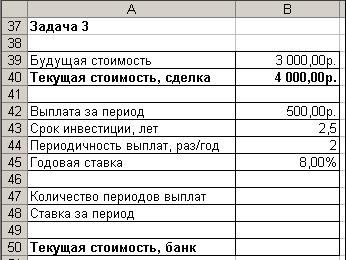
Рис. 21. Исходные данные для расчета текущей стоимости платежей и единовременной выплаты

4. Вычислите количество периодов выплат и ставку за период (рис. 22).

5. Вычислите текущую стоимость инвестиции. Результаты сравните с рис. 22.

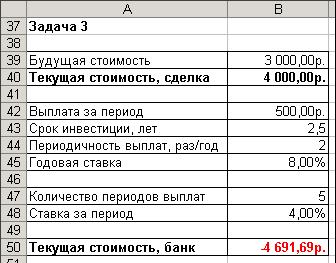
Рис. 22. Результаты вычисления текущей стоимости платежей и единовременной выплаты

6. Сохраните файл и продемонстрируйте результат преподавателю.

Анализ результатов решения

Функция возвращает значение –4 691,69. Это означает, что нужно вло-жить в банк 4 691,69 тг.под 8,0 % годовых. Поскольку значение 4 691,69 тг.больше, чем текущая стоимость сделки (4 000 р.), вложить деньги в сделку бо-лее выгодно, чем в банк.

Контрольное задание

Существует несколько вариантов вложения денежных средств с целью получения 70 000 тг.в течение 7 лет, величина годовой ставки – 12 %. Опре-делите наиболее выгодный вариант вложения денежных средств.

1. Сделка, которая каждые полгода возвращает 5 000 тг.

2. Сделка, в результате которой возвращается единовременная выплата в размере 70 000 тг.с начислением процентов каждые полгода.

3. Сделка, которая каждые полгода возвращает 2 500 тг.в течение сле-дующих 7 лет. Кроме того, в конце периода будет выплачено 40 000 тг.

Пояснения к задаче

Решение этой задачи требует оценить текущую стоимость вложения в банк по условиям указанных сделок и сравнить полученные значения с текущей стоимостью сделок. На основании сравнения необходимо сделать выводы о вы-годности вложений.

Ход решения задачи

1. Запустите Excel.

2. Переименуйте первый лист в ПС.

3. Оформите таблицы согласно (рис. 23).

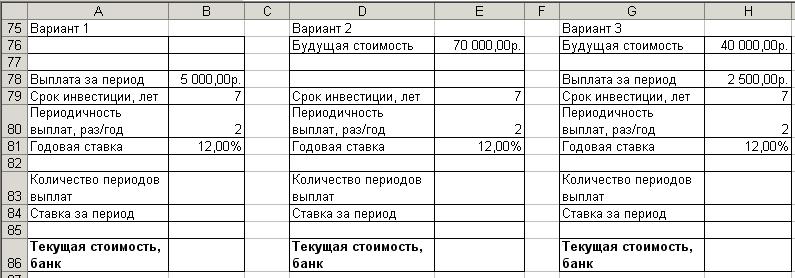
Рис. 23. Исходные данные для контрольного задания

4. Для каждого из вариантов вычислите текущую стоимость инвестиции.

5. Проанализируйте полученные значения, определите наиболее выгодный вариант вложения.

6. Сохраните файл и продемонстрируйте результат преподавателю.

3.2. Расчет будущей стоимости инвестиции. Функция БС (БЗ)

Функция БС (будущая стоимость) вычисляет для некоторого будущего момента времени величину вложения, которая образуется в результате едино-временной выплаты или/и ряда постоянных периодических платежей.

Синтаксис функции: БС(Ставка;Кпер;Плт;Пс;Тип).

Для определения будущего значения ряда выплат используется аргумент

Плт (выплата),аргумент Пс (приведенная стоимость) служит для определения будущего значения единовременной выплаты.

Задание 4 Определение наиболее выгодного варианта вложения денежных средств

Вкладчик планирует открыть счет сроком на 5 лет с ежемесячными пла-тежами и рассчитывает на среднюю скорость оборота 11 % в год. Выплаты производятся в начале периода. Существует несколько вариантов вложения:

1. Вносить на счет 2 000 тг.каждый месяц в течение 5 лет.

2. Вложить 100 000 тг.с целью получения по истечении 5 лет единовре-менной выплаты.

3. Внести на счет 30 000 р. и далее вносить на счет 1 500 тг.каждый ме-сяц в течение 5 лет.

Определите наиболее выгодный вариант вложения денежных средств.

Пояснения к задаче

Решение этой задачи требует оценить текущую стоимость вложения в банк по условиям указанных сделок и сравнить полученные значения с текущей стоимостью сделок. На основании сравнения необходимо сделать выводы о вы-годности вложений.

Для определения текущей стоимости вложения используется функция БС. Аргументу Тип задано значение 1 (вложения производятся в начале каждого периода).

Ход решения задачи

1. Запустите Excel.

2. Переименуйте первый лист в БС.

3. Оформите таблицы согласно (рис. 24).

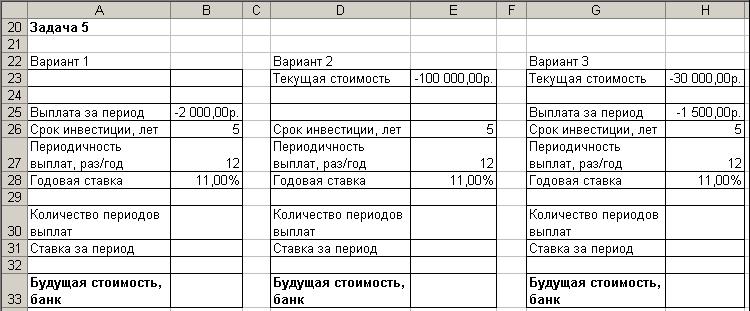
Рис. 24. Исходные данные для расчета будущих стоимостей инвестиций

4. Для каждого из вариантов вычислите будущую стоимость инвестиции.

5. Проанализируйте полученные значения, определите наиболее выгодный вариант вложения.

6. Сохраните файл и продемонстрируйте результат преподавателю.

3.3. Расчет периодического платежа. Функция ПЛТ (ППЛАТ)

Функция ПЛТ вычисляет размер периодической выплаты, необходимой для погашения ссуды за указанное число периодов.

Синтаксис функции: ПЛТ(Ставка;Кпер;Пс;Бс;Тип).

Задание 5 Определение величины периодического платежа

Взята ссуда размером 50 000 р. на срок 2 года под 6 % годовых с еже-квартальной выплатой платежей. Необходимо определить величину периоди-ческого платежа.

Ход решения задачи

1. Запустите Excel.

2. Переименуйте первый лист в ПЛТ.

3. Оформите таблицу согласно (рис. 25).

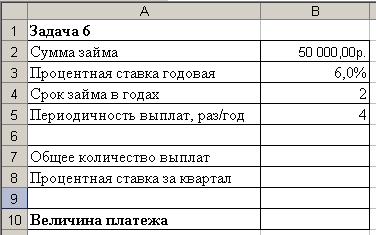
Рис. 25. Исходные данные для вычисления величины платежа

4. Вычислите количество периодов выплат и ставку за период (рис. 26).

5. Вычислите величину платежа. Результаты сравните с рис. 26.

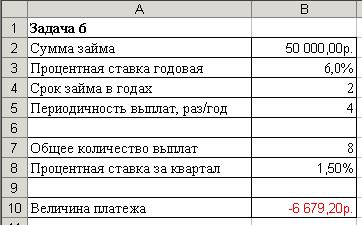
Рис. 26. Результаты вычисления величины платежа

6. Сохраните файл и продемонстрируйте результат преподавателю.

7. Составление графика погашения займа. Функции ПРПЛТ (ПЛПРОЦ), ОСПЛТ (ОСНПЛАТ)

Функция ПРПЛТ вычисляет платежи по процентам за заданный период при постоянных периодических выплатах и постоянной процентной ставке.

Синтаксис функции: ПРПЛТ(Ставка;Период;Кпер;Пс;Бс;Тип).

Функция ОСПЛТ вычисляет основные платежи за заданный период при постоянных периодических выплатах и постоянной процентной ставке.

Синтаксис функции: ОСПЛТ(Ставка;Период;Кпер;Пс;Бс;Тип).