Техника составления матрицы № 2.
Методика № 6. Социометрия.
Цель: изучить социометрический статус каждого ученика в классе, особенности взаимодействий, состав группировок.
Ход проведения
эксперимент проводится с учащимися всего класса. Каждому школьнику даётся лист бумаги. В правом верхнем углу ученики пишут свою фамилию. Учащимся зачитывается один из ниже перечисленных вопросов и предлагается ответить на него, записав фамилии троих своих одноклассников, кого бы они хотели бы выбрать для совместной деятельности.
Варианты вопросов:
1. С кем из одноклассников ты хотел бы сидеть за одной партой?
2. Если бы ваш класс реформировали, то с кем из своих одноклассников ты хотел бы продолжить учёбу?
3. Представьте, что вам предстоит интересное путешествие. С кем из одноклассников ты хотел бы его совершить?
Обработка: сначала определите статус каждого члена коллектива. Для этого все данные, полученные в ходе опроса, заносятся в матрицу №1.
Матрица № 1
| № | … | n | ||||||
| Апанович | + | + | ||||||
| Астровик | + | + | ||||||
| ... | ||||||||
| n | ||||||||
| Всего выборов | ||||||||
| Из них взаимных |
Далее следует подсчитать число выборов, полученных каждым учеником в результате эксперимента, и записать его в графе «Всего выборов». Затем на матрице отмечаются взаимные выборы, и отмечается их количество в графе «Из них взаимных». Проанализировав полученные результаты, дать характеристику социометрического статуса школьников на основе полученных ими выборов:
· «социометрические звёзды» - 6 и более выборов,
· «предпочитаемые» - 4-5 выборов,
· «принятые» - 1-3 выбора,
· «изолированные» - 0 выборов.
Высказать предположения о возможных причинах того или иного статуса ученика.
Данные матрицы позволяют вычислить коэффициент взаимности выборов (КВ):
Кол-во взаимных выборов
КВ = -------------------------------------  100%
100%
Общее кол-во выборов
Высокий показатель взаимности - 67-100%, средний показатель - 33-67%, низкий - 0-33%.
Далее следует определить уровень благополучия межличностных отношений, для чего сравнивают количество учащихся, имеющих низкий статус («принятые» и «изолированные»). Уровень благополучия считается высоким, если большинство учащихся имеют высокий статус; средним, если учащихся с высоким статусом столько же, сколько с более низким; низким - если число учащихся с низким статусом превышает число учащихся со средним и высоким статусом. Уровень благополучия межличностных отношений тем выше, чем меньше коэффициент изолированности (КИ), который вычисляется по формуле:
Кол-во изолированных учащихся
КИ = ------------------------------------------- 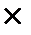 100%
100%
Общее кол-во учащихся
КИ считается высоким, начиная с 15%.
Данные социометрии могут быть использованы для определения микрогрупп в классном коллективе. Для этого на основании матрицы №1 составляется матрица №2, которая показывает микроклимат группы.
Матрица № 2
| № | Фамилия | … | n | ||||
| Апанович | + | + | |||||
| Астровик | + | ||||||
| Бобр | + | ||||||
| … | |||||||
| n |
Данная матрица позволяет определить кол-во микрогрупп в классе (они на матрице обведены), сопоставить официальные и не официальные микрогруппы. После этого необходимо дать характеристику неофициальных микрогрупп: их половой состав, причину объединения детей в микрогруппы, кто является лидером в ней, на чем основано лидерство, каков характер отношений в данной микрогруппе с другими и т.д.
Матрица №1
| № | Фамилия, имя | Всего | |||||||||||||||||||||
| Гладкий Клим | + | + | © | ||||||||||||||||||||
| Воробьёв Глеб | + | + | © | ||||||||||||||||||||
| Булавко Александр | © | © | © | ||||||||||||||||||||
| Деринговский Артём | © | + | © | ||||||||||||||||||||
| Вакулик Виктория | © | + | + | ||||||||||||||||||||
| Бохонко Анастасия | © | © | © | ||||||||||||||||||||
| Гончар Денис | © | © | + | ||||||||||||||||||||
| Мартинович Кирилл | © | © | © | ||||||||||||||||||||
| Невмержицкая Валерия | © | + | © | ||||||||||||||||||||
| Переходская Юлия | © | + | + | ||||||||||||||||||||
| Гайдаш Мелисса | + | + | + | ||||||||||||||||||||
| Зубрицкая Татьяна | + | + | + | ||||||||||||||||||||
| Шкурко Денис | + | + | + | ||||||||||||||||||||
| Уласевич Влад | © | © | + | ||||||||||||||||||||
| Ильюк Кристина | © | © | © | ||||||||||||||||||||
| Булова Анастасия | + | + | © | ||||||||||||||||||||
| Процко Александр | © | © | + | ||||||||||||||||||||
| Худой Павел | + | + | + | ||||||||||||||||||||
| Хлыстун Степан | + | + | + | ||||||||||||||||||||
| Осташев Слава | © | + | + | ||||||||||||||||||||
| Лупенко Анастасия | + | + | + | + | |||||||||||||||||||
| Всего выборов | - | - | |||||||||||||||||||||
| Из них взаимных | - | - | - | - | - |
Матрица №2
| № | Фамилия, имя | ||||||||||||||||||||||||
| 1. | Гладкий Клим | © | |||||||||||||||||||||||
| 20. | Осташев Слава | © | |||||||||||||||||||||||
| 2. | Воробьёв Глеб | © | |||||||||||||||||||||||
| 17. | Процко Александр | © | © | ||||||||||||||||||||||
| 4. | Дериговский Артём | © | © | ||||||||||||||||||||||
| 3. | Булавко Александр | © | © | © | |||||||||||||||||||||
| 7. | Гончар Денис | © | © | ||||||||||||||||||||||
| 8. | Мартинович Кирилл | © | © | © | |||||||||||||||||||||
| 14. | Уласевич Влад | © | © | ||||||||||||||||||||||
| 15. | Ильюк Кристина | © | © | © | |||||||||||||||||||||
| 9. | Невмержицкая Валерия | © | © | ||||||||||||||||||||||
| 6. | Бохонко Анастасия | © | |||||||||||||||||||||||
| 5. | Вакулик Виктория | © | |||||||||||||||||||||||
| 10. | Переходская Юлия | © | |||||||||||||||||||||||
| 16. | Булова Анастасия | © | |||||||||||||||||||||||
| 11. | Гайдаш Мелиса | ||||||||||||||||||||||||
| 12. | Зубрицкая Татьяна | ||||||||||||||||||||||||
| 13. | Шкурко Денис | ||||||||||||||||||||||||
| 18. | Худой Павел | ||||||||||||||||||||||||
| 19. | Хлыстун Степан | ||||||||||||||||||||||||
| 21. | Лупенко Анастасия | ||||||||||||||||||||||||
Микрогруппы в классе
Количество микрогрупп в классе – 2.
В первую микрогруппу входят Гресько Сергей, Давыдчик Евгений, Леончик Анна, Кожемяко Ксения. Лидер микрогруппы, Леончик Анна, существенно влияет на межличностные взаимоотношения в микрогруппе (но не в классе). Причина возникновения этой микрогруппы — общие интересы, а также в том, что ее некоторые члены живут в одном многоэтажном доме и хорошо знают друг друга.
Во вторую микрогруппу входят Жильская Ирина и Михед Елизавета. Явного лидера нет, общение происходит на одинаковом уровне. Это учащиеся с низким статусом. Причина возникновения этой микрогруппы — на основе общности интересов, дружбы.
В третью микрогруппу входят ЗборовскаяЕкатерина,Коржеский Антон, Минойть Вячеслав, Фролов Антон, Лаворенко Матвей, Понаморёва Полина, Панфиленко Ксения, Савенко Полина. Лидер данноймикрогруппы–Минойть Вячеслав – «социометрическая звезда», имеет высокий статус в классе. Другие члены микрогруппы имеют низкий статус, кроме Понаморёвой Полины. Лидерство Мийтя Вячеслава в микрогруппе основано на том, что это одни из наиболее популярных и активных учащихся класса. Причина возникновения этой микрогруппы – актив класса и на основе общности интересов, дружбы, особенно с девчонками, немаловажно, что они сидят вместе, рядом партами.
В четвертую микрогруппу входят КрысенкоАнасасия и Терех Юлия. Это учащиеся с низким статусом в группе. Эта микрогруппа не имеет выраженных лидеров, она возникла потому, что ее члены сидят за одной партой.
В пятую микрогруппу входят Лукина Ярослава и Фибик Юлиана. Явного лидера нет, общение происходит на одинаковом уровне. Это учащиеся с низким статусом. Причина возникновения этой микрогруппы — на основе общности интересов, дружбы.
В шесттуюмикрогруппу входят Понагайбо Анастасия и Яцко Татьяна. Это учащиеся с низким статусом в группе. Эта микрогруппа не имеет выраженных лидеров, она возникла потому, что ее члены сидят за одной партой.
В седьмую микрогруппу входят Суховеева Юлия и Сущик Ирина. Явного лидера нет, общение происходит на одинаковом уровне. Это учащиеся с низким статусом. Причина возникновения этой микрогруппы — на основе общности интересов, дружбы.
Аккерман Ирина и Палазник Валентина не входят ни в одну из данных микрогрупп.
Наиболее влиятельной, авторитетной является третья микрогруппа. Ее члены являются самыми уважаемыми в группе, так что их лидерство бесспорно. Это актив класса.
Имеет место эпизодическое соперничество первой и третьей микрогрупп.
Вывод:на основании данных полученных при проведении социометрии можно сделать анализ социометрического статуса каждого ученика в классе. «Социометрические звёзды» составляют 5% от общего количества. Это, как правило, учащиеся, отличающиеся своей яркостью, умом, общительностью, неординарностью, способностью объективно оценивать своих одноклассников и тактично указывать на недостатки, умением дать полезный совет и вовремя придти на помощь. «Предпочитаемые» составляют 30% от общего количества. Они отличаются жизнерадостностью, способностью настраивать класс на «хорошую волну», создавать «приподнятое» настроение, избежать «острых углов» в процессе обучения. «Принятые» составляют 65% от общего количества. Это учащиеся, для которых характерны следующие черты: робость, спокойный характер, неумение показать себя, выделить себя и свои качества, заниженная самооценка и неправильное представление о себе и своей значимости. Коэффициент взаимных выборов составляет 44,4%, т.е. является средненьким. Все это является следствием того, что раньше учащиеся учились в школах и не так давно образовали химико-биологический класс в лицее. Поскольку чем старше, тем труднее привыкать к смене обстановки, то некоторые ученики предпочитают проводить время с друзьями и подругами из своих старых классов, хотя в целом все учащиеся стараются общаться между собой.
Методика № 6. Социометрия.
Цель: изучить социометрический статус каждого ученика в классе, особенности взаимодействий, состав группировок.
Ход проведения
эксперимент проводится с учащимися всего класса. Каждому школьнику даётся лист бумаги. В правом верхнем углу ученики пишут свою фамилию. Учащимся зачитывается один из ниже перечисленных вопросов и предлагается ответить на него, записав фамилии троих своих одноклассников, кого бы они хотели бы выбрать для совместной деятельности.
Варианты вопросов:
1. С кем из одноклассников ты хотел бы сидеть за одной партой?
2. Если бы ваш класс реформировали, то с кем из своих одноклассников ты хотел бы продолжить учёбу?
3. Представьте, что вам предстоит интересное путешествие. С кем из одноклассников ты хотел бы его совершить?
Обработка: сначала определите статус каждого члена коллектива. Для этого все данные, полученные в ходе опроса, заносятся в матрицу №1.
Матрица № 1
| № | … | n | ||||||
| Апанович | + | + | ||||||
| Астровик | + | + | ||||||
| ... | ||||||||
| n | ||||||||
| Всего выборов | ||||||||
| Из них взаимных |
Далее следует подсчитать число выборов, полученных каждым учеником в результате эксперимента, и записать его в графе «Всего выборов». Затем на матрице отмечаются взаимные выборы, и отмечается их количество в графе «Из них взаимных». Проанализировав полученные результаты, дать характеристику социометрического статуса школьников на основе полученных ими выборов:
· «социометрические звёзды» - 6 и более выборов,
· «предпочитаемые» - 4-5 выборов,
· «принятые» - 1-3 выбора,
· «изолированные» - 0 выборов.
Высказать предположения о возможных причинах того или иного статуса ученика.
Данные матрицы позволяют вычислить коэффициент взаимности выборов (КВ):
Кол-во взаимных выборов
КВ = -------------------------------------  100%
100%
Общее кол-во выборов
Высокий показатель взаимности - 67-100%, средний показатель - 33-67%, низкий - 0-33%.
Далее следует определить уровень благополучия межличностных отношений, для чего сравнивают количество учащихся, имеющих низкий статус («принятые» и «изолированные»). Уровень благополучия считается высоким, если большинство учащихся имеют высокий статус; средним, если учащихся с высоким статусом столько же, сколько с более низким; низким - если число учащихся с низким статусом превышает число учащихся со средним и высоким статусом. Уровень благополучия межличностных отношений тем выше, чем меньше коэффициент изолированности (КИ), который вычисляется по формуле:
Кол-во изолированных учащихся
КИ = ------------------------------------------- 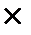 100%
100%
Общее кол-во учащихся
КИ считается высоким, начиная с 15%.
Данные социометрии могут быть использованы для определения микрогрупп в классном коллективе. Для этого на основании матрицы №1 составляется матрица №2, которая показывает микроклимат группы.
Техника составления матрицы № 2.
1. Заготовить сетку, аналогичную матрице №1.
2. Выделить в матрице №1 любого школьника, имеющий взаимный выбор с кем-либо из учеников.
3. Вписать, сохранив номер 1-й матрицы, его фамилию в первую строчку и в первую колонку, поставить его сохранившийся номер.
4. Во вторую строчку вписать фамилию ученика, оказавшегося во взаимном выборе. Фамилию вписать под тем номером, под которым, под которым он значится в матрице №1. Этот же номер проставляют во второй колонке.
5. В клетках пересечения этих двух номеров поставить знак взаимного выбора.
6. В последующих строчках и колонках вписываются фамилии и номера всех учеников, которые находятся во взаимном выборе с двумя предшествующими.
7. После того как исчерпан круг уч-ся, которые находятся во взаимном выборе, все значки, проставленные в матрице, обводятся жирной линией. Учащиеся, оказавшиеся в пределах этой линии составляют одну микрогруппу.
8. Аналогичная работа проделывается с остальными учащимися. В классе может быть несколько микрогрупп. Учащиеся, не имеющие взаимных выборов, записываются в конце матрицы.
Матрица № 2
| № | Фамилия | … | n | ||||
| Апанович | + | + | |||||
| Астровик | + | ||||||
| Бобр | + | ||||||
| … | |||||||
| n |
Данная матрица позволяет определить кол-во микрогрупп в классе (они на матрице обведены), сопоставить официальные и не официальные микрогруппы. После этого необходимо дать характеристику неофициальных микрогрупп: их половой состав, причину объединения детей в микрогруппы, кто является лидером в ней, на чем основано лидерство, каков характер отношений в данной микрогруппе с другими и т.д.
Матрица №1
| № | Фамилия, имя | Всего | |||||||||||||||||||||
| Гладкий Клим | + | + | © | ||||||||||||||||||||
| Воробьёв Глеб | + | + | © | ||||||||||||||||||||
| Булавко Александр | © | © | © | ||||||||||||||||||||
| Деринговский Артём | © | + | © | ||||||||||||||||||||
| Вакулик Виктория | © | + | + | ||||||||||||||||||||
| Бохонко Анастасия | © | © | © | ||||||||||||||||||||
| Гончар Денис | © | © | + | ||||||||||||||||||||
| Мартинович Кирилл | © | © | © | ||||||||||||||||||||
| Невмержицкая Валерия | © | + | © | ||||||||||||||||||||
| Переходская Юлия | © | + | + | ||||||||||||||||||||
| Гайдаш Мелисса | + | + | + | ||||||||||||||||||||
| Зубрицкая Татьяна | + | + | + | ||||||||||||||||||||
| Шкурко Денис | + | + | + | ||||||||||||||||||||
| Уласевич Влад | © | © | + | ||||||||||||||||||||
| Ильюк Кристина | © | © | © | ||||||||||||||||||||
| Булова Анастасия | + | + | © | ||||||||||||||||||||
| Процко Александр | © | © | + | ||||||||||||||||||||
| Худой Павел | + | + | + | ||||||||||||||||||||
| Хлыстун Степан | + | + | + | ||||||||||||||||||||
| Осташев Слава | © | + | + | ||||||||||||||||||||
| Лупенко Анастасия | + | + | + | + | |||||||||||||||||||
| Всего выборов | - | - | |||||||||||||||||||||
| Из них взаимных | - | - | - | - | - |
Матрица №2
| № | Фамилия, имя | ||||||||||||||||||||||||
| 1. | Гладкий Клим | © | |||||||||||||||||||||||
| 20. | Осташев Слава | © | |||||||||||||||||||||||
| 2. | Воробьёв Глеб | © | |||||||||||||||||||||||
| 17. | Процко Александр | © | © |
