Что такое репликационный портфель в теории оценки опционов?

Биномиальная модель: динамика цены лежащего в основе опциона объекта (актива) в течение срока действия опциона характеризуется биномиальным процессом. Метод использует возможность построения хеджированного портфеля, полностью эквивалентного опциону покупателя.

Так как возможны ровно два варианта изменения цены основного актива, то этот процесс называется биномиальным. Таким образом, моделируется стохастическое поведение стоимости проекта во времени.

После моделирования движения цены рассматриваемого актива формируется репликационный (хеджированный, эквивалентный) портфель. Целью его создания является использование комбинации безрискового актива (например, облигаций) и рассматриваемого актива для моделирования движения цены опциона. В данном случае применяются правила арбитража (т.е. не существует возможностей арбитража - возможности получения спекулятивной прибыли), и стоимость репликационного портфеля должна быть равна стоимости опциона.

В случае многопериодного биномиального процесса оценка опциона происходит итеративно. Она начинается с последнего периода и движется к началу дерева. На каждом временном отрезке создаются репликационные портфели для получения стоимости опциона в данном периоде. В результате аналитик получает стоимость опциона в текущий момент.

11. Приведите примеры инвестиционных стратегий «tail insurance» и поясните в чем заключаются риски данной стратегии.

Стратегия основывается на том, что изменения цен примерно соответствуют нормальному распределению:

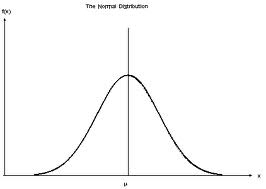
Тогда по бокам представлены «хвосты», которые отражают очень редко случающиеся события, в данном случае очень резкое изменение цен.

Стратегия заключается в том, что можно продавать опционы с очень отдалёнными от текущей цены страйками, предполагая, что за время жизни опциона цена так сильно не изменится. Тогда за продажу опциона можно просто так собирать премии – очень выгодно. Однако если очень редкое мегаизменение цены случится, то убытки по опциону могут многократно превзойти прибыли по премиям.

28. Разница между номинальными облигациями и индексируемыми на инфляцию называется breakeven spread. Какие премии в ценообразовании облигаций не позволяют утверждать напрямую, что это подразумеваемая инфляция?

Облигации, индексируемые на инфляцию, отличаются от обычных облигаций тем, что купоны скорректированы на инфляцию, то есть какая бы ни была инфляция, она будет выплачена.

Разница между доходностями обычных гос.облигаций и индексируемых на инфляцию называется breakeven spread. Данный спрэд не является подразумеваемой инфляцией, так как график доходностей облигаций искажен из-за наличия рисков. Риск неликвидности добавляет премию ликвидности у индексируемых облигаций, а риск высокой инфляции образует соответсвующую премию у обычных государственных облигаций.

29. Поясните понятия «грязная цена», НКД, дюрация. (Масленникова)

Накопленный купонный доход

Нако́пленный купо́нный дохо́д (НКД) — это часть купонного процентного дохода по облигации, рассчитываемая пропорционально количеству дней, прошедших от даты выпуска купонной облигации или даты выплаты предшествующего купонного дохода.

Формула расчета НКД подразумевает необходимость вычисления количества календарных дней от одной даты до другой или длительности периода, определяемого двумя датами. В зависимости от типа облигации, существует несколько базисов для расчета данных показателей, например «365/366», когда длительность периода от даты T1 до даты T2 определяется как разность дат: T2 – T1.

Размер накопленного купонного дохода можно выразить через размер купона в денежных единицах либо через ставку купона в процентах и номинал.

Стандартная формула для расчёта НКД по российским облигациям от ставки выглядит следующим образом:

НКД = N*С*T/B/100, где:

§ N — номинал

§ C — ставка текущего купона (в процентах годовых)

§ T — число дней с момента начала купонного периода по текущую дату

§ B — база расчёта (365 дней).

Вопрос

Если рыночная стоимость облигации равна 85 % от номинальной стоимости, годовой купон - 10 %. то по истечении 3 месяцев с момента выплаты купона, "грязная" цена облигации в процентах от номинальной стоимости составит:

§ А) 85%

§ В) 87,5%

§ С) 88,5%

§ D) 90%

Решение

Накопленный купонный доход (НКД).Когда облигация продается до наступления даты купонного платежа, купон уходит от продавца. В этом случае покупатель должен предоставить продавцу компенсацию соразмерно тому времени, которое прошло с последнего купонного платежа. НКД начисляется каждый день с момента последней выплаты купона. Чем ближе дата следующего купонного платежа, тем больше НКД. Размер НКД варьируется от нуля (купон только что был выплачен) до размера купона (купон должен быть выплачен сегодня). Купон рассчитывается пропорционально количеству дней, прошедших от даты выплаты предшествующего купонного дохода.

При покупке облигации покупатель оплачивает предыдущему владельцу НКД, таким образом, предыдущий владелец получает проценты за все дни владения облигацией с момента последней выплаты и не теряет их при продаже облигации.

Инвесторы могут видеть размер НКД в рублях для каждой облигации в своих биржевых терминалах, эти данные также поставляет биржа.

Грязная цена облигаций –это текущая рыночная цена облигации плюс накопленный купонный доход. При покупке облигации покупатель выплачивает именно грязную цену – в дополнение к рыночной цене он компенсирует предыдущему владельцу НКД.

85%+(10%/12мес)*3мес=87.5%

Дюрация облигации

Дюрация помогает определить степень зависимости рыночной цены облигации от изменения процентной ставки. Дюрация облигации приблизительно равна величине изменения цены облигации при изменении процентной ставки (ставки дисконтирования) на один процент. Другими словами, дюрация — это эластичность цены облигации по процентной ставке (ставке дисконтирования). Чем больше дюрация ценной бумаги, тем значительнее изменения ее рыночной стоимости при изменении процентной ставки (ставки дисконтирования). Следовательно, чем больше дюрация, тем выше риск процентной ставки.

Время, проходящее до наступления срока платежа по ценной бумаге, могло бы быть использовано для получения по этим инвестициям более высокого дохода. Следовательно, цена актива с более продолжительным сроком платежа имеет более сильную зависимость от процентной ставки (ставки дисконтирования), чем цена актива, по которому поток платежей происходит в ближайшем будущем. Ввиду существования такой зависимости, дюрация иногда измеряется как средневзвешенный срок до получения каждого платежа по ценной бумаге. Таким образом, дюрация бескупонной облигации со сроком погашения 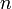лет — 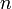лет, поскольку единственный платеж по ней будет произведен через 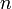лет. При наличии купонных выплат, дюрация меньше чем .

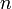Для облигаций дюрация рассчитывается следующим образом:

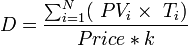
где

§ PV_i — это текущая (дисконтированная)стоимость будущих поступлений (купоны и основной долг) по облигации,

§ T_i — период поступления i-го дохода,

§ Price — цена облигации.

§ k - количество купонов в год

Из этой формулы следуют следующие закономерности изменения дюрации:

§ При прочих равных условиях, чем продолжительнее срок погашения облигации, тем больше дюрация.

§ При прочих равных условиях, при повышении ставки дисконтирования дюрация купонных облигаций уменьшается.

§ При прочих равных условиях, чем выше ставка купонных платежей по облигации, тем меньше дюрация.

Модифицированная дюрация

Модифицированная дюрация для облигации рассчитывается как:

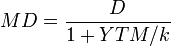
где

§ D — дюрация,

§ YTM — доходность к погашению

§ k - количество купонов в год

Практическое применение

Дюрация используется в частности для оценки процентного риска и риска реинвестирования по купонным облигациям. Как правило, инвесторы стараются поддерживать средневзвешенную дюрацию портфеля, равную горизонту инвестирования. Модифицированная дюрация позволяет оценить примерное изменение цены облигации (в %) в ответ на малое изменение рыночных процентных ставок (или доходности):