Если величина взноса равна проценту в денежном выражении, то величина шарового платежа равна сумме кредита.
Ая функция сложного процента - Текущая стоимость единицы (реверсии)
Текущая стоимость единицы — это величина, обратная накопленной сумме единицы, то есть текущая стоимость единицы, которая должна быть получена в будущем.
Процесс пересчета будущей стоимости капитала в настоящую носит название дисконтирование (от англ. Discount – уменьшать)? Ставка по которой происходит дисконтирование – ставка (коэффициент) дисконта.
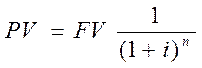
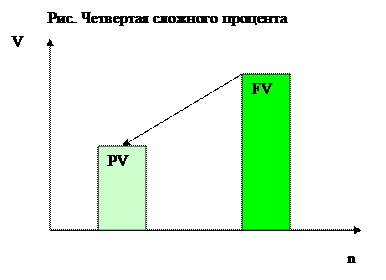
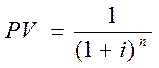
Пример 10. Сколько нужно вложить на счет в банке, приносящий 10% годовых, чтобы через 5 лет на нем было $100.
PV = 62,09.
При более частом накоплении:
Чем выше частота дисконтирования, тем меньше необходимая сумма текущей стоимости денежной единицы.
Ая функция сложного процента - Текущая стоимость аннуитета
Часто бывает так, что требуется оценить текущую стоимость серии платежей, т. е. аннуитета. Как и в случае будущей стоимости аннуитета, аннуитет может быть обычный и авансовый.
Очевидно, что текущая стоимость n-периодного обычного аннуитета равна сумме текущих стоимостей всех платежей.
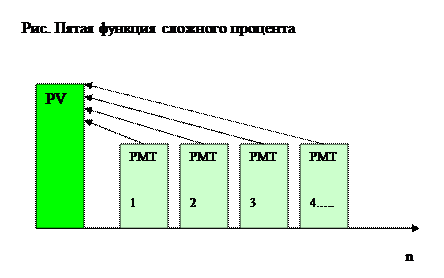
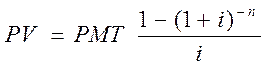
Пример 11. Ежегодный платеж за аренду дачи составляет $1000, ставка 10%, срок аренды 2 года. Определить текущую стоимость платежей.
PV = 1735,55.
Пример 12. У вас есть право получать с недвижимости в течение 5 лет каждый год в конце года 100 ден. Ед. чистой прибыли в виде рентного дохода. Сколько стоит это право сегодня при условии, что норма прибыли (ставка дисконтирования) 10%
PV = 379
Аналогично обычному аннуитету, вычисляется текущая стоимость для авансового аннуитета:
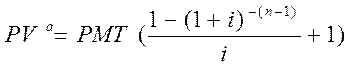
Пример 13. условие 2-ой задачи, получение происходит в начале года, PV = 417
Пример 14. Пусть, что при 12% годовых в течение 10 лет недвижимость будет приносить ежемесячный доход в размере 500 ден. Ед., после чего она будет продана за 40 000 ден.ед.. Сколько можно за нее заплатить сегодня?
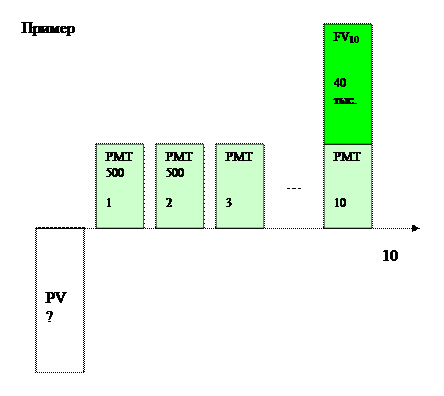
1) найдем текущую стоимость аннуитета = 34 850,26
2) найдем текущую стоимость продажи (реверсии)= 12 119,79
Общий ответ 46 970,05
Ая функция сложного процента - Взнос на амортизацию единицы
Амортизация — процесс погашения (ликвидации) долга в течение определенного периода времени.
Определение – Величина необходимых авансовых или обычных платежей (взносов) которая оплатит проценты и обеспечит полное погашение и возврат инвестиций в одну денежную в течение определенного количества временных периодов, определяемых процентной ставкой.
Данная функция позволяет определить, каким будет обязательный периодический платеж по кредиту, включающий выплату процентов и части основной суммы долга, и позволяющий погасить кредит в течение установленного срока.
Оказывается, для того, чтобы аннуитет погашал кредит, текущая стоимость этого аннуитета должна быть равна первоначальной сумме кредита. Используя формулу текущей стоимости аннуитета, мы можем получить величину периодического платежа — взноса на амортизацию капитала:
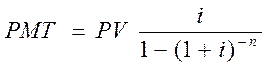
Каждый платеж состоит из двух частей:
РМТ = on + of,
