Понятия аккумулирования и дисконтирования базируются на определении сложного процента.
Стоимость денег во времени
Как оценить экономическую эффективность инвестиций? Очевидным является факт, что деньги, полученные через год или несколько лет, имеют меньшую стоимость, чем та же сумма денег в текущий момент времени, независимо от экономической ситуации и прогнозов на ее дальнейшее развитие. Это различие текущей и будущей стоимости денег связано с тем, что сумма, полученная на какой-либо период времени раньше, чем аналогичная сумма, полученная позднее, может быть положена на банковский депозит под проценты и в момент получения второй сравниваемой суммы первая будет больше на величину накопленных за период между получением обеих сумм процентов.
При оценке денежных потоков используется временная теория денег: денежные потоки, возникающие в разные моменты времени приводятся к одному моменту времени.
Процессы преобразования текущей и будущей стоимости называются аккумулированием и дисконтированием. Аккумулирование — это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что эта сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент. Дисконтирование — это процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
Понятия аккумулирования и дисконтирования базируются на определении сложного процента.
Сложный процент — это процент начислений как на основную сумму, так и на невыплаченные проценты, начисленные за предыдущий период. Логика сложного процента очевидна:
— все деньги, которые оставлены на депозите, должны приносить процент;
— процент приносят только те деньги, которые оставлены на депозите.
Основной предмет финансовой математики — шесть функций денег (или шесть функций сложного процента). Перечислим эти шесть функций и их обозначения в экономических формулах:
Будущая стоимость единицы (накопленная сумма единицы) - FV (Future value).
2. Будущая стоимость аннуитета (накопление единицы за период) - FVA (Future value of an annuity).
3. Фактор фонда возмещения - SFF (Sinking fund factor).
4. Текущая стоимость единицы (реверсии) — PV (Present value).
5. Текущая стоимость аннуитета - PVA (Present value of annuity).
6. Взнос на амортизацию единицы - IAO (Installment of amortize one).
Эти функции используются в различных финансовых расчетах. В дальнейшем будет подробно рассмотрена каждая из этих функций с точки зрения ее математической формулировки и сферы применения.
Формула сложных процентов
Во всех вычислениях с использованием сложного процента используется формула:
Sn=(l+i)n,
где Sn - сумма после n периодов;
i — периодическая ставка дохода;
N — количество периодов накоплений.
Сложный процент – это экономическая категория, используемая для сопоставления одной и той же суммы денег в различные периоды времени с учетом того, что в каждом периоде доход приносит не только первоначальную сумму вклада, но и процент от нее.
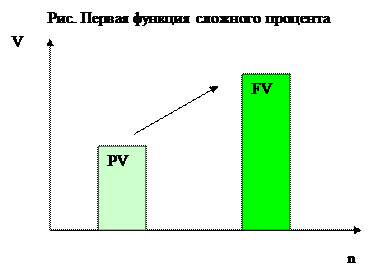
На рис. Представлена графическая иллюстрация формул простого и сложного процента
|

Первая функция сложного процента - Будущая стоимость денежной единицы (накопленная сумма единицы)
PV — текущая стоимость денег.
Пример 1. $1000 вложено в банк под 10 % годовых. Какая сумма накопится на счете через 5 лет?
FV = 1000(l + 0,l)5 =1610,5,
Правило 72-х.
Иногда при расчетах приходится сталкиваться с задачей определения количества периодов начисления, по истечении которых первоначально депонированная сумма увеличивается вдвое. Очень просто решить эту задачу позволяет известное выражение:
"Правило 72-х", в основу которого положены логарифмы. Количество периодов, необходимое для удвоения первоначальной суммы вычисляется так:
n = 72 / i
Авансовый аннуитет
Теперь перейдем к рассмотрению авансового аннуитета. Как и в случае обычного, рассмотрим накопленные суммы в конце первого, второго ... n-ro периода:
FV1 = РМТ • (1 + i),
FV2 =PMT-(l + i)2+PMT-(l + i),
FV3 =PMT-(l + i)3+PMT-(l + i)2+PMT-(l + i),
FVn =PMT-(l + i)n+PMT-(l + i)n~1+... + PMT-(l + i)2+PMT-(l + i). Применив формулу суммы геометрической прогрессии, получаем:
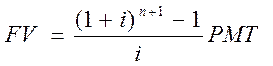
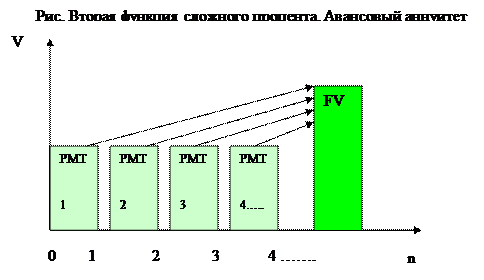
Пример 6. Чтобы заработать себе на пенсию, вы решили откладывать в банк в начале каждого года по 100 денежных единиц. Сколько денег Вы снимите со счета через 5 лет, если банк начисляет 10% ежегодно?
| Год | Взнос в начале года | Сумма вклада на начало года | Сумма дохода вклада | Сумма вклада на начало года |
| 100,00 | 100,00 | 10,00 | 110,00 | |
| 100,00 | 210,00 | 21,00 | 231,00 | |
| 100,00 | 331,00 | 33,10 | 364,10 | |
| 100,00 | 464,10 | 46,41 | 510,51 | |
| 100,00 | 610,51 | 61,05 | 671,56 |
Шаровый платеж
Понятие шаровый платеж – представьте себе, что Вы взяли в кредит на N лет под I% годовых. По условиям кредита Вы должны каждый месяц вносить какой-либо оговоренный взнос, а в конце N-года погасить всю оставшуюся сумму. Величина этой суммы и называется шаровый платеж.
Общий ответ 46 970,05
Данная функция позволяет определить, каким будет обязательный периодический платеж по кредиту, включающий выплату процентов и части основной суммы долга, и позволяющий погасить кредит в течение установленного срока.
Оказывается, для того, чтобы аннуитет погашал кредит, текущая стоимость этого аннуитета должна быть равна первоначальной сумме кредита. Используя формулу текущей стоимости аннуитета, мы можем получить величину периодического платежа — взноса на амортизацию капитала:
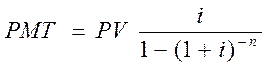
Каждый платеж состоит из двух частей:
РМТ = on + of,
ПРАКТИКУМ
Временная теория денег
Задание №1.
Индейцы продали о. Манхэттен в 1626 году за товары стоимостью $24. Какая сумма накопилась бы на счете сегодня, если бы они вложили эти деньги в банк под 6% годовых. Используйте технику простого и сложного процента.
Задание №2.
Стоимость земли, купленной за $8000 повышается на 15% в год (по сложному проценту). Сколько она будет стоить через 3 года.
Задача №3.
Предприниматель только что заплатил $100 за опцион на покупку земли. Опцион дает ему право приобрести собственность за $10000 по истечении двух лет. Уже выплаченные за опцион $100 не будут включены в цену покупки. Какую сумму сегодня необходимо положить в банк, выплачивающий 10% годовых при ежеполугодовом накоплении с тем, чтобы через два года иметь нужную сумму для приобретения собственности?
Задача №4.
Вкладчик хочет получить $8000, вложив сегодня $1000 под 12% годовых. Сколько полных платежных периодов понадобится для осуществления цели?
Задание №5.
Пенсионный фонд принимает взносы под 10% годовых. Какая сумма будет накоплена к выходу на пенсию, если из зарплаты в конце каждого из 10 лет перечислять в пенсионный фонд $500.
Задача №6.
Каждый месяц вы получаете от квартиры сданной в аренду $50. Эти деньги вы вкладываете в банк под 10% годовых. Сколько денег у вас будет через 5 лет? Задание №7.
Молодая семья планирует купить квартиру через 5 лет. Ее доходы позволяют в начале каждого года вкладывать в банк $1000 под 10% годовых. Сколько денег будет на счете через 5 лет.
Задание №8.
Владелец жилой недвижимости планирует заменить кровлю на своих зданиях через 5 лет. Он полагает, что через 5 лет это ему обойдется в $20000. Какую сумму он должен депонировать по окончании каждого года с учетом того, что средства на счете будут накапливаться по годовой ставке 10%.
Задача №9.
Через 5 лет понадобится $20000. Какую сумму депонировать в начале каждого года на счет в банк, начисляющий 10% годовых?
Задание №10.
Сколько надо положить на счет в банк под 10% годовых, чтобы через 10 лет купить квартиру за $30000.
Задача №11.
Через 7 лет необходимо иметь $3000. Достаточно ли положить в банк $1200, если он начисляет процент ежеквартально, годовая ставка равна 10%.
Задание №12.
Земельный спекулянт рассчитывает, что через 2 года массив площадью 10 га может быть продан за $1000 за га. Какая сегодняшняя цена позволит спекулянту получить 15% годовой доход.
Задача №13.
Определить сумму сегодняшних инвестиций, дающих право ежегодного получения $100 дохода в конце каждого года на протяжении 4 лет при ставке дисконта 10%. Сделать проверку, используя "метод депозитной книжки".
Задача №14.
Какова текущая стоимость ипотечного кредита, предусматривающего выплату $1000 в начале каждого года в течение 15 лет. Ставка дисконта 10%.
Задание №15.
Аренда магазина принесет его вкладчику в течение первых трех лет ежегодный доход $3000, в последующие 5 лет доход составит $4500. Определить текущую стоимость совокупного дохода, если ставка дисконта 10%.
Задание №16.
Какую сумму целесообразно заплатить инвестору за объект недвижимости, который можно эффективно эксплуатировать в течение 5 лет. Объект в конце каждого года приносит доход по 350000 руб. Требуемый доход на инвестиции — 20%. Проверить методом "депозитной книжки".
Задание №17.
Рассчитать величину ежегодного взноса в погашение кредита в сумме $15000, предоставленного на 5 лет под 10% годовых.
Задание №18.
Банк предоставляет кредит $10000. Его нужно погашать в конце каждого полугодия в течение 2 лет. Кредит предоставлен под 10% годовых. Каким будет каждый полугодовой платеж.
Задание №19.
Какое вложение денег является наиболее выгодным:
a) приобретение права аренды магазина за $30000 на 7 лет, магазин приносит ежегодно $8000 чистого операционного дохода;
b) вложить $30000 в банк под 10% годовых.
Задание №20.
Строительная фирма предлагает вам квартиру на таких условиях. Вы в течение 25 лет ежегодно выплачиваете $4000 при ставке ипотеки 10%. Оценщик оценил вашу квартиру в $30000. Согласитесь ли вы на этот контракт.
Задание №21.
Отдельно стоящий магазин для розничной торговли сдан в аренду на 25 лет за $5000 в год, вносимых в конце каждого года. У арендатора есть опцион на покупку здания по истечении срока аренды за $65000. В этом случае инвесторы стремятся к получению 10%-ного дохода на инвестиции. Какова текущая стоимость объекта.
Задание №22.
Вы выиграли конкурс. По его условиям вы можете получить $1000 сейчас наличными или $2000 — через 5 лет. Какой приз вы выберете, если банк принимает вклады под 10% годовых?
Ипотечное кредитование
Задание №1.
Однокомнатная квартира стоит $9000 в наличии имеется $2000. Недостающую сумму решено взять в банке под 20% годовых на 5 лет. Составить схему погашения ипотечного кредита.
Задание №2.
Кредит в размере $1000 выдан на 4 года под 12% годовых. Возмещение основной суммы кредита происходит ежегодно равными частями. Построить схему погашения кредита.
Задание №3.
Начальная сумма кредита $30000, срок кредита 5 лет, начальная норма процента - 10%. Начальная норма будет скорректирована в сторону увеличения на 1% в конце 1 года и еще на 2% в конце второго года, далее не изменится. Построить схему погашения кредита.
Задание №4.
Сумма кредита равна $25000, номинальная ставка определена в 10%, ежегодный платеж должен составлять $2651,98. Какое время потребуется для полной амортизации кредита. Постройте таблицу погашения кредита на первые 3 года.
Задание №5.
Стоимость объекта недвижимости $250000. Коэффициент ипотечной задолженности — 40%. Кредит предоставлен на 5 лет под 5% годовых и предусматривает периодическую выплату только процентов. Однако через 5 лет должна быть единовременно погашена вся основная сумма кредита. Заемщик хочет в конце каждого года вносить в банк определенную сумму с тем, чтобы иметь возможность выплачивать проценты по кредиту и погасить долг через 5 лет. Банк начисляет ежегодно 10% годовых. Какую сумму необходимо вносить в банк для погашения кредита.
Задача №6.
Ипотечный кредит на сумму $50000 выдан на 15 лет при 10% годовых и ежегодных платежах. За досрочное погашение кредита предусмотрен штраф в размере 8% от невыплаченной суммы кредита. Определить действительную норму процента по кредиту при условии его досрочного погашения в конце 3 года.
Задача №7.
Господин Иванов купил квартиру стоимостью $20000 с привлечением ипотечного кредита. При оформлении сделки он заплатил фирме $3000, а остальные обязался выплатить в течение года под 35% в год. Определите сумму ежемесячных платежей по кредиту.
Стоимость денег во времени
Как оценить экономическую эффективность инвестиций? Очевидным является факт, что деньги, полученные через год или несколько лет, имеют меньшую стоимость, чем та же сумма денег в текущий момент времени, независимо от экономической ситуации и прогнозов на ее дальнейшее развитие. Это различие текущей и будущей стоимости денег связано с тем, что сумма, полученная на какой-либо период времени раньше, чем аналогичная сумма, полученная позднее, может быть положена на банковский депозит под проценты и в момент получения второй сравниваемой суммы первая будет больше на величину накопленных за период между получением обеих сумм процентов.
При оценке денежных потоков используется временная теория денег: денежные потоки, возникающие в разные моменты времени приводятся к одному моменту времени.
Процессы преобразования текущей и будущей стоимости называются аккумулированием и дисконтированием. Аккумулирование — это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что эта сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент. Дисконтирование — это процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
Понятия аккумулирования и дисконтирования базируются на определении сложного процента.
Сложный процент — это процент начислений как на основную сумму, так и на невыплаченные проценты, начисленные за предыдущий период. Логика сложного процента очевидна:
— все деньги, которые оставлены на депозите, должны приносить процент;
— процент приносят только те деньги, которые оставлены на депозите.
Основной предмет финансовой математики — шесть функций денег (или шесть функций сложного процента). Перечислим эти шесть функций и их обозначения в экономических формулах:
