Степень взаимосвязи доходностей двух активов
При формировании портфеля степень взаимосвязи между доходностями двух активов можно определить с помощью показателей ковариации и корреляции.
Ковариация (covariance) – это статистическая мера взаимодействия двух случайных величин. Она говорит о степени зависимости двух переменных, например о зависимости доходностей двух ценных бумаг А и В.
Ковариация может принимать как положительные, так и отрицательные значения. При положительной ковариации доходностей двух бумаг с ростом доходности первой доходность второй будет расти. И наоборот, при падении доходности первой – доходность второй будет снижаться. При отрицательной ковариации рост доходности первой бумаги будет сопровождаться падением второй. Если ковариация равна нулю, то никакой зависимости не наблюдается либо она очень слаба. Чем больше значение ковариации, тем сильнее зависимость. Ковариация определяется по формуле:

| где | r(1,2)i. — доходность актива 1 или 2 в i-ом периоде, |
| E(ri1,2) — средняя (ожидаемая) доходность актива 1 или 2 за n периодов. |
Если необходимо рассчитать выборочную ковариацию, то приведенную формулу необходимо разделить на n периодов наблюдения (см. формулу выборочной дисперсии).
Ковариация зависит от единиц измерения величин, что ограничивает ее применение. Очень близкой к ковариации является другая статистическая мера – коэффициент корреляции (correlation coefficient). Он нормирует ковариацию для облегчения сравнения с другими парами независимых переменных. Ковариация двух случайных величин равна корреляции между ними, умноженной на произведение стандартных отклонений. Отсюда, коэффициент корреляции равен:

Коэффициент корреляции  является безразмерной величиной и принимает значение от +1 до -1. В большинстве случаев он находится между двумя этими экстремальными значениями. Для независимых случайных величин корреляция близка к нулю.
является безразмерной величиной и принимает значение от +1 до -1. В большинстве случаев он находится между двумя этими экстремальными значениями. Для независимых случайных величин корреляция близка к нулю.
Пример: Портфель инвестора состоит из двух активов: А и В. Инвестор планирует три исхода событий в будущем, характеристики которых приведены в таблице. Определить коэффициент корреляции между двумя активами.
| Вероятность | Доходность актива А | Доходность актива В | |
| Исход 1 | 0,5 | 40% | - 20% |
| Исход 2 | 0,3 | ||
| Исход 3 | 0,2 | - 30% | 40% |
Решение:
1. E(ra) = 40*0,5+0*0,3+(-30*0,2) = 14%
2. E(rв) = (-20*0,5)+0*0,3+40*0,2 = -2%
3. Сovа,b = (40-14)(-20+2)+(0-14)(0+2)+(-30-14)(40+2)=-2344
4.  = (40-14)2+ (0-14)2+ (-30-14)2 =676+196+1936=2808;
= (40-14)2+ (0-14)2+ (-30-14)2 =676+196+1936=2808;  = 52,99
= 52,99
5.  = (-20+2)2 + (0+2)2 + (40+2)2=324+4+1764=209;
= (-20+2)2 + (0+2)2 + (40+2)2=324+4+1764=209;  = 45,74
= 45,74
6.  = -2344/52,99*45,74= - 0,967
= -2344/52,99*45,74= - 0,967
При расчете риска портфеля, состоящего из нескольких активов, необходимо учесть парные ковариации (корреляции) всех входящих в него активов.
Дисперсия портфеля на основе ковариации доходностей, например для трех активов входящих в портфель, определяется по формуле:

Каждый член двойной суммы включает в себя произведение весов двух ценных бумаг и их ковариацию.
Пример: Российский инвестор купил акции компании A на 600 тыс. долл., компании В на 400 тыс. долл. Стандартное отклонение доходности акции компании A в расчете на день составляет 1,4%, компании В – 1,55%. Курс доллара 1долл.=25 руб., стандартное отклонение валютного курса в расчете на один день 0,43%, коэффициент ковариации между курсом доллара и доходностью акции компании A равен 0,0903, доходностью компании В – 0,05332. Ковариация доходностей акции компании A и компании В равна 1,736. Определить стандартное отклонение доходности портфеля в расчете на день.
Решение: Риск инвестора обусловлен 3 факторами, которые необходимо учесть при расчете: падением курса доллара, а также возможным падением котировок акций компаний А и В. Валютный риск учитывается полностью, поэтому его удельный вес принимается равным единице.
1.  = 600/1000=0,6;
= 600/1000=0,6;  = 400/1000=0,4;
= 400/1000=0,4;
2.  =12*0,432+0,62*1,42+0,42*1,552+2*1*0,6*0,0903+2*1*0,4*0,05332+2*0,6*0,4*1,736=2,259196;
=12*0,432+0,62*1,42+0,42*1,552+2*1*0,6*0,0903+2*1*0,4*0,05332+2*0,6*0,4*1,736=2,259196;
3.  =
=  = 1,503%.
= 1,503%.
Несложные алгебраические вычисления позволяют понять интерпретацию коэффициента корреляции:
§ при объединении в портфель активов с корреляцией +1 риск не уменьшается, а лишь усредняется;
§ идеальный портфель состоит из активов с корреляцией -1;
§ при отрицательной корреляции между активами риск портфеля меньше средневзвешенной суммы рисков, привносимых каждым конкретным активом, поэтому при формировании портфеля необходимо стремиться к объединению активов с наименьшей корреляцией доходностей. Этот частный случай диверсификации называется хеджированием.
Коэффициент бета
Относительное изменение доходности акции (портфеля акций) по сравнению с доходностью рынка, характеризуется коэффициентом бета – β. Этот коэффициент измеряет относительную неустойчивость доходности актива (портфеля) в сравнении с репрезентативным показателем доходности рынка в целом (например, каким-либо представительным индексом рынка или фьючерсом на него). Математический смысл коэффициента β следует из формулы оптимального (эффективного) портфеля:

| где |  – ставка без риска; – ставка без риска; |
 – коэффициент бета актива; – коэффициент бета актива; | |
 – ожидаемая доходность по рынку за тот же период. – ожидаемая доходность по рынку за тот же период. |
Исходя из этой формулы, теория инвестиционного портфеля позволяет сделать вывод: премия за риск любого актива, включенного в оптимальный портфель, пропорциональна премии за риск, связанной с портфелем в целом. Коэффициентом пропорциональности выступает β.
Бета портфеля представляет собой средневзвешенную сумму значений бета активов, его составляющих:

Т.к. бета портфеля является средним значением беты ценных бумаг, входящих в портфель, то нет оснований предполагать, что увеличение диверсификации портфеля вызовет изменение беты портфеля, и, соответственно, рыночного риска портфеля в какую-либо сторону. Диверсификация портфеля позволяет усреднить рыночный риск.
Бета конкретного актива рассчитывается по формуле:

| где |  – корреляция между доходностью i-го актива и доходностью на рыночный индекс; – корреляция между доходностью i-го актива и доходностью на рыночный индекс; |
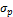 – стандартное отклонение доходности на рыночный индекс; – стандартное отклонение доходности на рыночный индекс; | |
 – ковариация доходности i-го актива и доходности на рыночный индекс; – ковариация доходности i-го актива и доходности на рыночный индекс; | |
 – дисперсия доходности на рыночный индекс. – дисперсия доходности на рыночный индекс. |
Бета портфеля показывает, как рынок будет действовать на изменение доходности портфеля. Например, если бета портфеля равна 5, то увеличение доходности по рынку на 1% приведет к увеличению доходности портфеля на 5%. Такая же величина изменения риска, но в обратном направлении, приведет к снижению доходности портфеля на те же 5%.
Таким образом, активы с β > 1 более рискованны, чем с β < 1. С точки зрения ограничения рыночных рисков при формировании портфеля активы с отрицательной β более предпочтительны. Стремясь сформировать портфель с наименьшим β можно использовать индексный метод, когда структура формируемого портфеля копирует структуру какого-либо фондового индекса с широкой базой и пересматривается с его изменениями.
Пример: Доходность акции компании А и рыночного портфеля за четыре года представлены в таблице. Определить коэффициент бета акции относительного рыночного портфеля на основе смещенных оценок.
| Годы | ||||
| Доходность актива А | -2 | -1 | ||
| Доходность рыночного портфеля | -4 | -2 |
Решение:
1.  = 0,75
= 0,75
2.  = 0,5
= 0,5
3. 
4. 
5.  = 7,875/14,6875=0,53617
= 7,875/14,6875=0,53617
