Выпуклость эффективного множества
Для того чтобы понять, почему эффективное множество является выпуклым, рассмотрим следующий пример портфеля из двух ценных бумаг. Ценная бумага А имеет ожидаемую доходность в 5 % и стандартное отклонение в 20 %.Вторая ценная бумага G имеет ожидаемую доходность 15 % и стандартное отклонение 40 %. Теперь рассмотрим все возможные портфели, состоящие из этих ценных бумаг. Пусть Х1 – доля бумаг А, Х2 = 1- Х1 – доля бумаг G.
| Доля / портфель | A | B | C | D | E | F | G |
| Х1 | 1,00 | 0,83 | 0,67 | 0,50 | 0,33 | 0,17 | 0,00 |
| Х2 | 0,00 | 0,17 | 0,33 | 0,50 | 0,67 | 0,83 | 1,00 |
 |
Для того чтобы рассмотреть возможные инвестиции в эти семь портфелей, необходимо вычислить их ожидаемые доходности и стандартные отклонения.
Доходность составит:
| Портфель | rA= | rB= | rC= | rD= | rE= | rF= | rG= |
| Доходность | 5,00% | 6,70% | 8,30% | 10,00% | 11,70% | 13,30% | 15,00% |
 |
Для вычисления стандартных отклонений данных портфелей необходимо применить уравнение:
 |
Это составит:
 |
Но так как:
где ρij – коэффициент корреляции (он всегда находится в пределе [-1:1]), то скажем для портфеля D границы отклонения составят 10% и 30%.
| Портфель | A | B | C | D | E | F | G |
| Нижняя граница σр | 20,00% | 9,80% | 0,20% | 10,00% | 20,20% | 29,80% | 40,00% |
| Верхняя граница σр | 20,00% | 23,40% | 26,60% | 30,00% | 33,40% | 36,60% | 40,00% |
 |
Интересен тот факт, что все верхние пограничные значения лежат на прямой линии, соединяющей точки А и G (коэффициент корреляции равен 1). Это означает, что любой портфель, составленный из этих двух бумаг, не может иметь стандартное отклонение, соответствующее точке, лежащей правее прямой линии, соединяющей эти две ценные бумаги. Вместо этого значение стандартного отклонения должно лежать на этой прямой линии или левее нее. Это означает желательность диверсификации портфеля. А именно, диверсификации ведет к уменьшению риска, так как стандартное отклонение портфеля будет в общем случае меньше, чем средневзвешенное стандартное отклонение бумаг, входящих в портфель.
Следует сказать, что любой портфель, состоящий из этих двух ценных бумаг, лежит в пределах границ треугольника, изображенного на рисунке. Его фактическое местоположение зависит от значения коэффициента корреляции между этими двумя ценными бумагами.
В реальности коэффициенты корреляции между двумя ценными бумагами отличаются от крайних значений. Вот, например, что получится если представить, что коэффициент корреляции равен «-0,5» и «0,5» (множество точек более приближенных к оси ординат соответствуют коэффициенту корреляции «-0,5»):

Рыночная модель
Предположим, что доходность обыкновенной акции за данный период времени (например, месяц) связана с доходностью за данный период акции на рыночный индекс. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции, а с падением рыночного индекса, вероятно, будет падать и цена акции. Один из путей отражения данной взаимосвязи носит название рыночная модель:
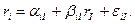 |
где ri, - доходность ценной бумаги i за данный период;
rI - доходность на рыночный индекс I за этот же период;
аiI - коэффициент смещения;
βiI - коэффициент наклона;
ε iI - случайная погрешность.
Предположив, что коэффициент наклона положителен, из уравнения можно заметить следующее: чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги.
«Бета»-коэффициент
Отметим, что наклон в рыночной модели ценной бумаги измеряет чувствительность ее доходности к доходности на рыночный индекс.
Коэффициент наклона рыночной модели часто называют «бета»-коэффициентом и вычисляют так:
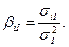 |
где σiI обозначает ковариацию между доходностью акции i и доходностью на рыночный индекс, а σ2I обозначает дисперсию доходности на индекс. Акция, которая имеет доходность, являющуюся зеркальным отражением доходности на индекс, будет иметь «бета»-коэффициент, равный 1. То есть акции с «бета»-коэффициентом больше единицы обладают большей изменчивостью, чем рыночный индекс, и носят название «агрессивные» акции. И наоборот, акции с «бета»-коэффициентом меньше единицы, обладают меньшей изменчивостью, чем рыночный индекс, и называются «оборонительными» акциями.
Диверсификация
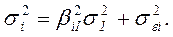 |
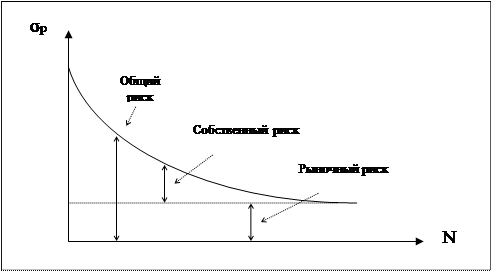
Исходя из рыночной модели, общий риск ценной бумаги i, измеряемый ее дисперсией, состоит из двух частей: (1) рыночный (или систематический) риск, (2) собственный (или несистематический) риск. Таким образом:
Увеличение диверсификации может привести к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же.
 |
