Теорема об эффективном множестве
Из набора N ценных бумаг можно сформировать бесконечное число портфелей. Необходимо ли инвестору проводить оценку всех этих портфелей? Нет. Объяснение того факта, что инвестор должен рассмотреть только подмножество возможных портфелей, содержится в следующей теореме об эффективном множестве:
Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых:
1. Обеспечивает максимальную ожидаемую доходность для некоторого уровня риска.
2. Обеспечивает минимальный риск для некоторого значения ожидаемой доходности.
Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством, или эффективной границей.
Достижимое множество
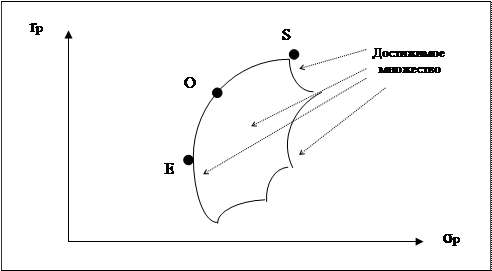
Рисунок ниже представляет иллюстрацию местоположения достижимого множества, также известного как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы в N ценных бумаг. Это означает, что все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества.
 |
Теорема об эффективном множестве в применении к достижимому множеству
Теперь можно определить местоположение эффективного множества, применив теорему об эффективном множестве к достижимому множеству. Сначала выделим множество портфелей, удовлетворяющих первому условию теоремы об эффективном множестве. Если посмотреть на рисунок, то можно заметить, что не существует менее рискового портфеля, чем портфель Е. Это объясняется тем, что если провести через Е вертикальную прямую, то ни одна точка достижимого множества не будет лежать левее данной прямой.
Рассматривая далее второе условие, можно заметить, что не существует портфеля, обеспечивающего большую ожидаемую доходность, чем портфель S, потому что ни одна из точек достижимого множества не лежит выше горизонтальной прямой, проходящей через S.
Учитывая то, что оба условия должны приниматься во внимание при определении эффективного множества, отметим, что нас удовлетворяют только портфели, лежащие на верхней и левой границе достижимого множества между точками Е и S. Соответственно эти портфели составляют эффективное множество, и из этого множества эффективных портфелей инвестор будет выбирать оптимальный для себя. Все остальные достижимые портфели являются неэффективными портфелями, поэтому мы их можем игнорировать.
Выбор оптимального портфеля
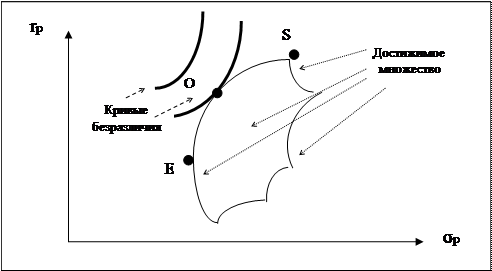
Для выбора оптимального портфеля инвестор должен нарисовать свои кривые безразличия на одном рисунке с эффективным множеством, а затем приступить к выбору портфеля, расположенного на кривой безразличия, находящейся выше и левее остальных. Этот портфель будет соответствовать точке, в которой кривая безразличия касается эффективного множества. Как это видно из рисунке ниже, таким портфелем является портфель О. Несомненно, что инвестор предпочел бы портфель, находящийся на более высокой кривой безразличия, но такого достижимого портфеля просто не существует. Желание находиться на какой-то конкретной кривой не может быть реализовано, если данная кривая нигде не пересекает множество достижимости.
 |
