Discount rate. Federal funds rate, Treasury bill rates, Treasury notes rates, Treasury bond rates.

Соответственно, в русском переводе:

Дисконтная ставка, Ставка по федеральным фондам, Ставки по казначейским векселям, Ставки по казначейс­ким обязательствам, Ставки по государственным облига­циям США

Процентные ставки в этой цепочке растут слева на­право.

Дисконтная ставка FED (Discount rate) - самый силь­ный инструмент и к ее изменению FED прибегает редко; за всю историю FED, с 1934 года, дисконтная ставка ме­нялась 114 раз (последнее изменение с 4,5 до 4,75% годо­вых состоялось 24 августа 1999 года). Более гибкий меха­низм управления осуществляется черезставку по феде­ральным фондам (Federal Funds Rate) - процентную став­ку, по которой банки, члены Федеральной резервной си­стемы торгуют друг с другом краткосрочными кредита­ми федеральных фондов. Если дисконтная ставка уста­навливается высшим руководящим органом - Советом управляющих FED, то ставка по федеральным фондам находится в компетенции Комитета по операциям на от­крытом рынке (Federal Open Market Committee, FOMC). В конечном счете, доходности финансовых инструментов определяются рынком, но процентные ставки централь­ного банка дают сильнейший ориентир для всех прочих ставок, что подтверждается наблюдаемой очень сильной корреляцией между Federal Funds Rate и доходностями государственных облигаций, в особенности - краткосроч­ных. На двух рисунках ниже представлена общая дина­мика FED Funds и график доходности государственных ценных бумаг США на примере 10-летних облигаций.

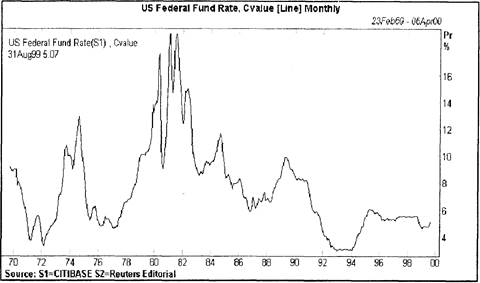
Рис. 5.4. Процентные ставки по федеральным фондам США

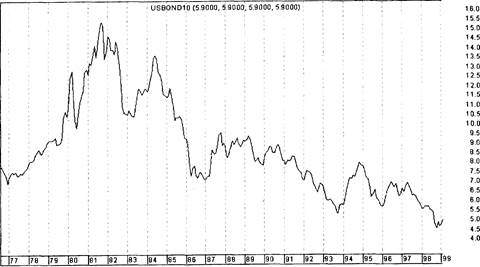
Рис. 5.5. График доходности 10-летних государственных облигаций США (10-year Treasury bonds rates)

&

Основные положения количественной теории денег

Количество денег, находящихся в обращении, тесно связано с потребностью в них для обеспечения торгового оборота, кредита, инвестиций, международных расчетов. Стремление к устойчивости экономического развития требует поддержания денежной массы в определенной пропорции к производимому объему товаров и услуг, так как нарушение пропорций ведет к многим проблемам. Это соотношение пропорциональности принято записывать в виде уравнения, называемого основным уравнением количественной теории денег:

М * V = Р * Q,

где М - объем денег в обращении, V - скорость обраще­ния денег, Q - объем выпуска в экономике (реальный ВВП), Р - средний уровень цен в стране.

Для установления связи величины М с обменным курсом полезно сравнить два таких уравнения, записан­ных для двух стран; если индексом f обозначить показа­тели для иностранной экономики, а индексом d - для на­циональной экономики, то из двух полученных уравне­ний

Mf*Vf=Pf*Qf, Md*Vd=Pd*Qd

можно составить выражение для обменного курса двух валют,

Pd Md Qf Vd

S = —— = —————,

Pf Mf Qd Vf

выраженного в количестве единиц национальной валю­ты за одну единицу иностранной валюты. Это простое уравнение наглядно показывает, что изменение соотно­шения Md/Мf объёмов денежной массы в двух странах (при сохранении других параметров обращения денег) есте­ственным образом влечет изменение взаимного курса двух рассматриваемых валют.

Точно также, как при выводе относительного вари­анта паритета покупательной способности (параграф 3), и здесь можно перейти к относительным изменениям ве­личин (имевшим место за некоторый промежуток време­ни от t до t + Т); если считать, что изменяются только показатели денежной массы, а изменениями прочих па­раметров пренебречь (δQ=0, δV=0), то получим связь от­носительного изменения обменного курса с относитель­ными изменениями объемов денежной массы:

δS = δMd - δMf;

здесь

M(t+T) - M(t)

dM = ——————————

M(t)

(соответственно, для d и для f).

Если, например, денежная масса по евро за некото­рый период выросла на 4,5%, а по доллару на 8,0%, то это означает, что курс евро/доллар должен за этот период измениться (вырасти) на

δS = δMf - δMd = 8,0 - 4,5 = 3,5%;

(в данном случае мы переставили слагаемые в формуле, поскольку евро котируется в виде "количество долларов за 1 евро").

Задача.

Для тех читателей, кто имеет доступ к историческим данным по денежным агрегатам (через систему Reuters или другого поставщика экономической статистики), предлагается построить соответствующие графики пока­зателей М и оценить по ним темпы роста М для основ­ных валют. С помощью приведенной выше формулы най­ти оценки относительного изменения обменных курсов выбранных пар валют, обусловленного ростом денежной массы.

Процентный дифференциал

Главный фактор, прямо и непосредственно опреде­ляющий курс одной валюты по отношению к другой - это разность в процентных ставках, действующих по двум валютам(Interest Rate Differential).

Пусть клиент банка имеет 1 миллион евро, которые на срок 3 месяца освобождены из оборота фирмы и мо­гут быть размещены в депозит для получения дохода. При этом предположим, что процентные ставки по евро 2.65 процента годовых, а по доллару действуют более высо­кие ставки в 5.28 процентов. Тогда, конвертировав евро в доллары, можно получить больший доход. Допустим, сегодняшний курс евро EUR= 1.0400$. Если разместить сумму 1 миллион евро в депозит, то через 3 месяца будет получена сумма

2.62 90

1 + —— * ———— = 1,00655 миллионов евро.

100 360

Если же конвертировать 1 миллион евро в доллары по курсу EUR и разместить их в долларовый депозит, то

будет получена сумма

5.28 90

EUR (1 + —— * —— ) = 1,04 * 1,0132 = 1,053728 млн. $

100 360

Если бы курс евро за эти 3 месяца остался бы тем же EUR= 1.0400$, то результат второго варианта в евро рав­нялся 1,0132, а разность суммы, полученной от конверта­ции полученных долларов назад в евро, и полученного в первом варианте результата, 1,0132 - 1,00655 = 0,00665 миллионов = 6650 евро, составляла бы выгоду от перево­да евро в доллар и долларовой депозитной операции, полученную за счет разности в процентных ставках по доллару и по евро.

В более общем случае, когда инвестор сравнивает два варианта:

1. размещение суммы S в некоторой валюте под i1 процентов годовых и

2. конвертация этой суммы в другую валюту с разме­щением в депозит под i2 процентов годовых на срок в t дней, то разница между результатами этих двух вариантов со­ставит величину, пропорциональную процентному диф­ференциалу (U - i2)(Interest rate Differential):

S(il-i2) t /36000