Методичні рекомендації до розв‘язування задач

Приклад 1. Які з чисел 234, 634, 104 конгруентні числу 9 за модулем 25.

Розв‘язання. Віднімемо від даних чисел число 9. Дістанемо:

234 – 9= 225, 634 – 9=625, 104 – 9=95. Числа 225 і 625 діляться на 25, тому числа 234 і 634 конгруентні числу 9 за модулем 25, тобто

, .

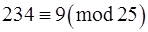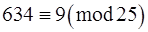Приклад 2. Довести, що .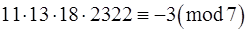

Розв‘язання. Скористуємося другою властивістю конгруенцій за одним і тим самим модулем. Розглянемо почленно конгруенції

, , , ,

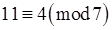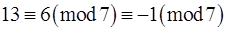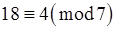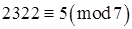Помножимо всі одержані конгруенції

.

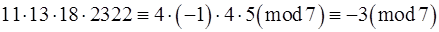Отже, .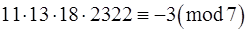

Приклад 3. Знайти остачу від ділення 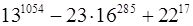на .

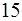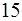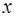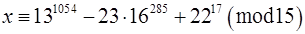Розв‘язання. Скористаємося властивостями конгруенцій за модулем . Нам треба знайти таке ціле невід‘ємне число , що і 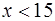. оскільки 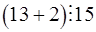, то 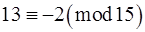, тобто .

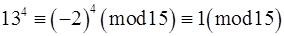За властивостями .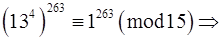

. (*)

,

. (**)

, , .

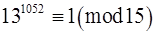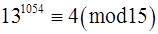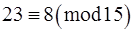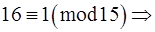
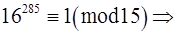
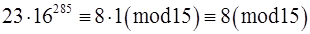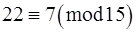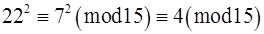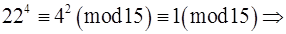
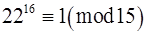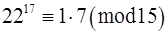(ù)

Виконаємо дії додавання та віднімання над конгруенціями (*),(**),(ù).

(*) – (**) + (ù),

+

.

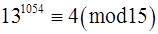
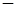
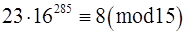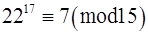
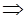
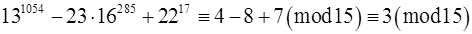Отже, число 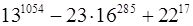при діленні на 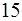дає остачу .

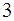Приклад 4. Розв’язати в цілих числах рівняння.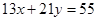

Так як НСД(13,21)=1, то дане рівняння має безліч розв’язків. Підбором встановлюємо частинний розв’язок .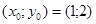

Тоді загальний розв’язок має вигляд .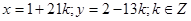

Відповідь: .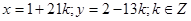

Приклад 5. Розв’язати в цілих числах рівняння.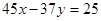

Так як НСД(45;37)=1, то рівняння має безліч розв’язків.

Щоб знайти 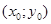застосуємо алгоритм Евкліда:

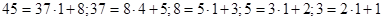. Отже 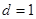. Запишемо алгоритм Евкліда в зворотньому напрямку (лінійне представлення):

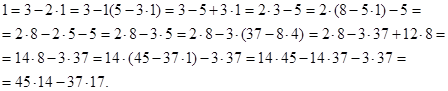
Отже (14;17) частинний розв’язок рівняння .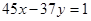

Тоді 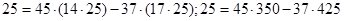тобто .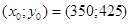

Отже всі розв’язки знайдемо за формулами .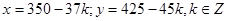

Відповідь: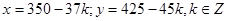

Приклад 6. Розв’язати в цілих числах рівняння.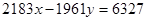

Знайдемо НСД(2183;1961)= 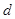для цього скористаємося алгоритмом Евкліда.

.

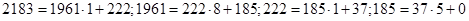Отже, .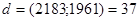

Запишемо алгоритм Евкліда в зворотньому напрямку:

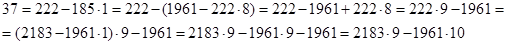
Отже 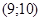- частинний розв’язок рівняння .

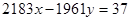Тоді 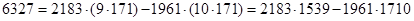, тобто 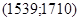частинний розв’язок рівняння .

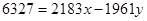Загальний розв’язок має вигляд: .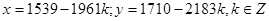

Відповідь: .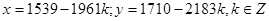

Приклад 7. Розв’язати конгруенцію.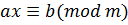

Нехай 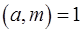, нехай 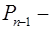чисельник передостаннього підхідного дробу 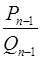для числа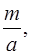 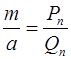. Оскільки 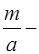нескоротний дріб, то 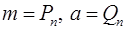. За властивостей підхідних дробів маємо .

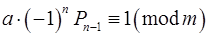Розглянемо приклад 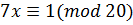маємо таблицю, де 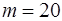, , 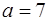, 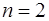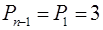. Тоді ;

.

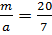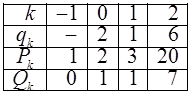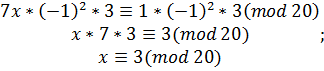
Приклад 12 Розв’язати конгруенцію. .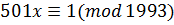

Розв‘язання. .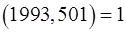

Розкладемо дріб 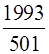у ланцюговий дріб і знайдемо 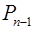та .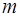

За алгоритмом Евкліді дістанемо

1993=501*3+490; n=0;

501=490*1+11; n=1;

490=11*44+6; n=2;

11=6*1+5; n=3;

6=5*1+1; n=4;

5=1*5+0; n=5;

Отже, , .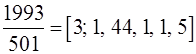

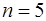Для обчислення , складемо таблицю

k	-1
qk	+ ///////
Pk		*
Qk

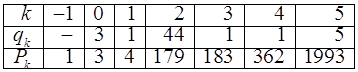Звідси .

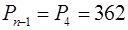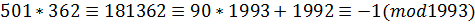
Відповідь.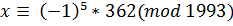

Приклад. Варіант 30.

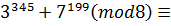
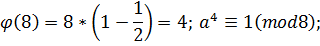
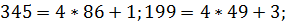
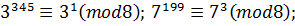
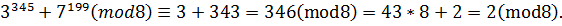
Остача від ділення 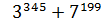на 8 дорівнює 2.

Приклад. Варіант 30.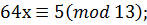

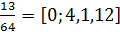
13=64*0+13 64=13*4+12 13=12*1+1 12=1*12+0

k -1 qk /////// Pk Qk

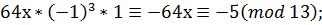
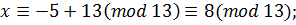
Перевірка: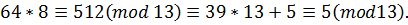

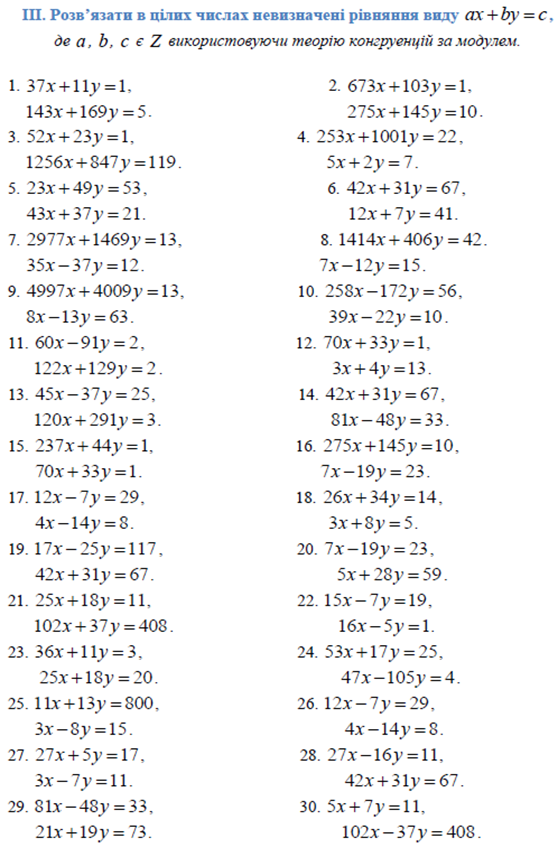
Приклад. Варіант 30. 1) 5x+7y=11;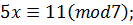

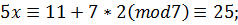
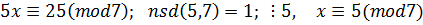; x=7t+5;

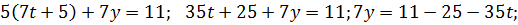
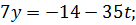
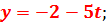
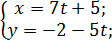
t	-2	-1
x	-9	-2				-9
y			-2	-7	-12

Відповідь: (-9,8),(-2,3),(5,-2),(12,-7),(19,-12),(-9,8),…

2) 102x-37y=408;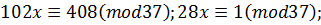

37/28=[1;3,9] 37=28*1+9 28=9*3+1 9=1*9+0

k -1 qk /////// Pk Qk

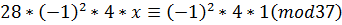
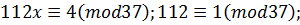
x=37t+4;

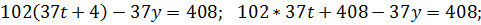
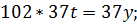
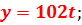
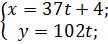
t	-2	-1
x	-70	-33				-70
y	-204	-102				-204

Відповідь: (-70,-204),(-33,-102),(4,0),(41,102),(78,204),(-70,-204),….

Приклад. Варіант 30. 4.5m=450cm

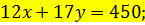
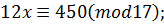
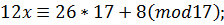
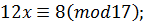
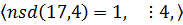
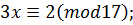
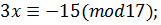
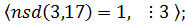
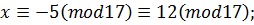
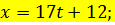
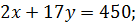
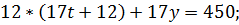
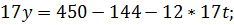
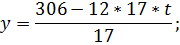
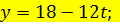
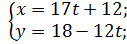
t	-2	-1
x	-22	-5
y					-6	-18

Відповідь. Так як відємної кількості дошок неможе бути, тоді відповідь має міститися в додатніх розвязках (12,18) або (29,6).