Введення в теорію алгоритмів

Слово «алгоритм» походить від імені великого середньоазіатського вченого Мухаммеда аль-Хорезмі, який жив у першій половині IX століття (точні роки його життя невідомі, але вважається, що він народився близько 780 року, а помер близько 850). «Аль-Хорезмі» означає «з Хорезму» (історичної області в нинішньому Узбекистані, центром якої було місто Хіва).

Близько 825 року аль-Хорезмі написав твір, в якому вперше дав опис придуманої в Індії позиційної десяткової системи числення. На жаль, арабський оригінал його книги не зберігся, так що її оригінальна назва нам невідомо. Аль-Хорезмі сформулював правила обчислень в новій системі і, ймовірно, вперше використав цифру 0 для позначення пропущеної позиції в записі числа (її індійське назву араби переклали як as-sifr або просто sifr, звідси такі слова, як цифра і шифр). Приблизно в цей же час індійські цифри почали застосовувати й інші арабські вчені. У першій половині XII століття книга аль-Хорезмі в латинському перекладі проникла в Європу. Перекладач, ім'я якого до нас не дійшло, дав їй назву «Algoritmi de numero Indorum» («Індійське мистецтво рахунки, твір аль-Хорезмі»).

Близько 1250 року англійський астроном і математик Іоанн Сакробоско (Johannes de Sacrobosco, ок. 1200-1256) написав працю з арифметики «Algorismus vulgaris», на сторіччя став основним підручником з обчисленням у десятковій позиційній системі числення в багатьох європейських університетах. У вступі Сакробоско назвав автором науки про рахунок мудреця на ім'я Алгус (Algus). А в популярній середньовічної поеми «Роман про троянду» (1275-1280) Жана де Мена «грецький філософ Алгус» ставиться в один ряд з Платоном, Аристотелем, Евклідом і Птолемеєм! Зустрічався також варіант написання імені Аргус (Argus). І хоча згідно давньогрецької міфології корабель «Арго» був побудований Ясоном, саме цьому Арго приписувалося будівництво корабля.

Багато століть абак був фактично єдиним засобом для практичних обчислень, ним користувалися всі: і купці, і міняйли, і вчені. Гідності обчислень на лічильної дошці роз'яснював у своїх творах такий видатний мислитель, як Герберт Орільякскій (938-1003), що став в 999 році папою римським під ім'ям Сильвестра II. Нове з величезною працею пробивав собі дорогу, і в історію математики увійшло наполегливе протистояння таборів абацістов і алгорісміков (перші іноді ще називали гербекістамі), які пропагували використання для обчислень замість абака арабських цифр.

Однак поступово значення слова розширювалося. Учені починали застосовувати його не тільки до суто обчислювальним, але і до інших математичних процедур. Наприклад, близько 1360 року французький філософ Микола Орем (Nicolaus Oresme, 1323/25-1382) написав математичний трактат «Algorismus proportionum» («Обчислення пропорцій»), в якому вперше використав ступеня з дробовими показниками і фактично впритул підійшов до ідеї логарифмів. Коли ж на зміну абаку прийшов так званий рахунок на лініях, численні керівництва по ньому стали називати «Algorithmus linealis», тобто правила рахунку на лініях.

Можна звернути увагу на те, що первісна форма algorismi через якийсь час втратила останню букву, і слово набуло більш зручне для європейського вимови вид algorism. Пізніше і воно, в свою чергу, піддалося спотворенню, швидше за все, пов'язаному зі словом arithmetic.

У 1684 році Г. В. Лейбніц у творі «Nova Methodvs pro maximis et minimis, itemque tangentibus ...» вперше використав слово «алгоритм» (Algorithmo) в ще більш широкому сенсі: як систематичний спосіб вирішення проблем диференціального обчислення.

У XVIII столітті в одному з німецьких математичних словників, Vollstandiges mathematisches Lexicon (виданому в Лейпцігу в 1747 р.) термін algorithmus все ще пояснюється як поняття про чотири арифметичних операціях. Але таке значення не було єдиним, адже термінологія математичної науки в ті часи ще тільки формувалася. Зокрема, вираз algorithmus infinitesimalis застосовувалося до способів виконання дій з нескінченно малими величинами. Користувався словом алгоритм і Л. Ейлер, одна з робіт якого так і називається - «Використання нового алгоритму для вирішення проблеми Пелля» («De usu novi algorithmi in problemate Pelliano solvendo»). Ми бачимо, що розуміння Ейлером алгоритму як синоніма способу вирішення завдання вже дуже близько до сучасного.

Алгоритми ставали предметом все більш пильної уваги вчених, і поступово це поняття посіло одне з центральних місць у сучасній математиці. Що ж стосується людей, від математики далеких, то до початку сорокових років XX століття це слово вони могли почути хіба що під час навчання в школі, в поєднанні «алгоритм Евкліда». Незважаючи на це, алгоритм все ще сприймався як термін суто спеціальний, що підтверджується відсутністю відповідних статей в менш об'ємних виданнях. Зокрема, його немає навіть в десятитомной Малої Радянської Енциклопедії (1957 рік), не кажучи вже про однотомних енциклопедичний словник. Але зате через десять років, в третьому виданні Вікіпедія (1969 рік) алгоритм вже характеризується як одна з основних категорій математики, «не володіють формальним визначенням у термінах більш простих понять, і абстрагіруемих безпосередньо з досвіду». Як ми бачимо, відмінність навіть від трактування першим виданням Вікіпедія разюча! За сорок років алгоритм перетворився в одне з ключових понять математики, і визнанням цього стало включення слова вже не в енциклопедії, а в словники. Наприклад, воно присутнє в академічному «Словнику російської мови» (1981 рік) саме як термін з області математики.

Одночасно з розвитком поняття алгоритму поступово відбувалася і його експансія з чистої математики в інші сфери. І початок їй поклала поява комп'ютерів, завдяки якому слово «алгоритм» знайшло нове життя. Взагалі можна сказати, що його сьогоднішня популярність напряму пов'язана зі ступенем поширення комп'ютерів. Наприклад, у третьому томі «Дитячої енциклопедії» (1959 рік) про обчислювальних машинах говориться чимало, але вони ще не стали чимось звичним і сприймаються скоріше як певний атрибут світлого, але досить далекого майбутнього. Відповідно і алгоритми жодного разу не згадуються на її сторінках. Але вже на початку 70-х років XX століття, коли комп'ютери перестали бути екзотичною новинкою, слово «алгоритм» стрімко входить в ужиток. Це чуйно фіксують енциклопедичні видання. В «Енциклопедії кібернетики» (1974 рік) у статті «Алгоритм» він вже пов'язується з реалізацією на обчислювальних машинах, а в «Радянській військовій енциклопедії» (1976 рік) навіть з'являється окрема стаття «Алгоритм рішення задачі на ЕОМ».

Визначення алгоритму теж змінювалося у часі залежно від того, за допомогою яких понять формулюється це визначення. Тому використовується значна кількість визначень алгоритму. Наведемо одне з них.
Під алгоритмом розуміють скінченну сукупність правил дій, які виконуються у певному порядку для розв’язання всіх задач даного класу.
Чому це визначення алгоритму не є абсолютно строгим математично? Бо нема чіткого визначення поняття всіх задач даного класу. Які задачі можна віднести до одного класу? Ті, що виникають в одній предметній області? Ті, що використовують інформацію одного типу? Чи операції одного типу?
Для багатьох задач можна побудувати послідовність операцій їх розв’язання. Якщо цю послідовність можна використати для розв’язання подібних задач, то вона наближається до алгоритму. Щоб вона ним стала, необхідно, щоб вона набула властивостей алгоритму:
— дискретність, тобто розчленованість алгоритму на окремі операції;
— детермінованість, тобто однозначна визначеність результату кожної операції, не залежна від виконавця;
— масовість— можливість застосування до будь-яких вхідних даних задач виділеного класу;
— результативність— скінченність процесу перетворення інформації.
Щоб побудувати алгоритм, необхідно дотримуватись певних умов:
— вхідні та вихідні дані задаються у вигляді послідовності слів;
— процес розв’язання задачі це є процес перетворення вхідних даних у вихідні;
— процес перетворення складається із сукупності елементарних припустимих операцій формального характеру;
— припустима елементарна операція — це проста, чисто механічна дія, результат якої не залежить від виконавця (машини чи людини);
— послідовність припустимих операцій не залежить від конкретних вхідних даних;
— порядок виконання припустимих операцій визначений однозначно;
сукупність припустимих операцій визначається класом задач та типом даних.
Отже, кожна елементарна операція для будь-якої вхідної інформації визначає вихідну інформацію за певними правилами. Для того, щоб будувати алгоритми, застосовувати їх, робити їх порівняння, оцінювати і вибирати найбільш прийнятний у кожному окремому випадку, необхідно мати якісь загальні засоби представлення алгоритмів. Для цього вводяться деякі поняття. І, перш за все, — засоби для представлення інформації. Послідовності слів на вході та виході алгоритму складаються з символів. Які символи для цього використовуються? Залежно від того, які символи ми обираємо, інформацію буде неоднаково представлено і операції перетворення інформації будуть різними. Введемо поняття алфавіту.
Абстрактним алфавітом називають будь-яку скінченну сукупність об’єктів, які називають символами (літерами) цього алфавіту.
Ці символи самі по собі не мають ніякого змісту, властивостей та смислу. Це можуть бути літери алфавіту будь-якої природної мови, цифри, малюнки, значки тощо. Отже, абстрактних алфавітів може бути безліч. Більш того, при розв’язанні однієї задачі можна використовувати декілька алфавітів (вхідний, вихідний, проміжний), навіть розширювати їх, об’єднувати. Але серед них є такі, що використовуються для представлення різних типів інформації, — їх називають стандартними. Найбільш поширеним серед них є двійковий алфавіт {0,1}, який набув найбільшого значення з винаходом та використанням електронних обчислювальних машин для розв’язан­ня задач обробки інформації.
Слово в абстрактному алфавіті — це будь-яка скінченна впорядкована послідовність із його символів.
Кількість символів у слові — його довжина. Якщо довжина дорівнює нулю, то слово називають пустим (0).

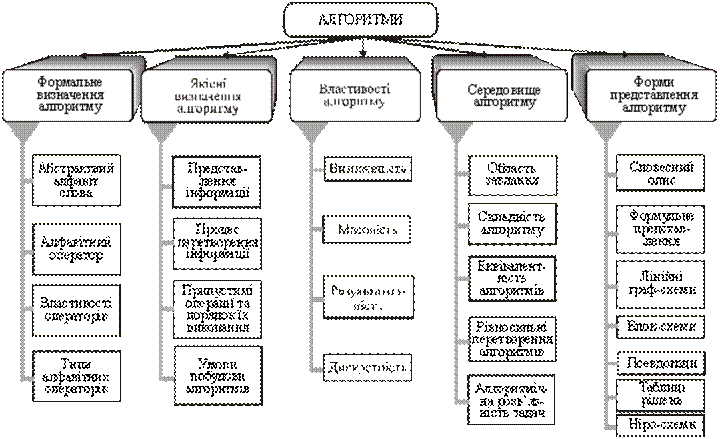
Рис. 1.1. Структурний взаємозв’язок основних понять та елементів, що становлять суть алгоритму