Глава 3. Методологические принципы

Физического происхождения

Развитие физики в 20-м веке оказало одно из наиболее значительных влияний на формирование философии и методологии науки. В этой главе мы приводим примеры некоторых методологических принципов, истоки определения или нового понимания которых восходят к развитию неклассической физики.

§ 1. Принцип наблюдаемости

Усиление актуальности проблемы наблюдения в современной науке связано, как это ни странно, с появлением в составе современного научного познания повышенно ненаблюдаемых объектов. Таковы, например, элементарные частицы (особенно такие из них, как кварки или суперструны), антиматерия в атомной физике, черные дыры, Вселенная в целом в астрофизике, бессознательное в современной психологии, и т.д. Особенно проблематичной оказалась ситуация с процессом наблюдения в современной квантовой физике. Микрообъекты, если так можно выразиться, представляют из себя уже настолько «чувствительные» сущности, что их невозможно наблюдать и измерять, не внося существенных изменений в сам способ их существования. Так, по крайней мере, утверждается в господствующей сегодня интерпретации квантовой теории. В этом случае уже не может быть выполнен принцип нейтральности наблюдения. Наблюдается уже не столько объект, сколько результат его взаимодействия со средствами и субъектом наблюдения. Процесс наблюдения оказывается одновременно «приготовлением» объекта в определенном состоянии. Такая ситуация, кстати говоря, очень напоминает некоторые случаи, хорошо известные нам из психологии. Например, если мы начнем думать, что человек Х плохой и начнем выказывать по отношению к нему соответствующее поведение, то человек Х, почувствовав такого рода негативную установку, может разозлиться и в самом деле проявить себя плохо. И вот здесь возникает вопрос: человек Х является плохим или лишь проявил себя плохим, поддерживая навязываемый ему стереотип поведения ? Нечто подобное возникает и с микрообъектами. Когда мы наблюдаем их проявления, у нас уже не может быть полной уверенности, что наблюдаемые свойства являются свойствами самих объектов, а не навязаны этим объектам условиями наблюдения. Продолжая аналогию, можно было бы постараться наблюдать человека Х более аккуратно – так, чтобы он не догадывался о наблюдении или чтобы не навязывать ему какой-то стереотип поведения. Для этого нужно сделать средства наблюдения менее активными и явными. И вот тут-то и возникает проблема, специфическая именно для квантовой физики. Дело в том, что в этой теории утверждается наличие некоторого минимума активности (так называемого «кванта действия»), меньше которого нельзя снизить меру активности. Причем, активности самих микрообъектов также могут быть настолько малыми, что они оказываются сравнимыми с нижним порогом активности вообще. В таких условиях невозможно сделать наблюдение менее активным, и активность наблюдения оказывается сравнимой с активностью самого объекта наблюдения.

В такой ситуации можно было бы, по-видимому, двигаться в двух основных направлениях. Во-первых, можно попытаться смириться с такого рода ситуацией. Тогда нужно отказаться от попытки наблюдать объект-сам-по-себе. Приходится принять, что единственным объектом, с которым можно иметь дело, является тот объект (объект-для-нас), который наблюдаем в «активном» наблюдении. Именно такого рода точка зрения на природу наблюдения господствует в современной квантовой физике. Во-вторых, можно предположить, что есть возможность и более «тонкого» наблюдения, которое пока нам недоступно, но которое, в принципе, могло бы не нарушать существование даже «чувствительных» микрообъектов. Хотя и эта точка зрения присуща некоторым физикам, но сегодня она является не общепринятой.

Принятие первой точки зрения приводит к повышению значимости процесса наблюдения в составе научного знания, поскольку условия наблюдения теперь не отбрасываются как строительные леса после построения научной теории, но эти условия оказываются теперь во многом входящими в состав самой теории, определяющими саму структуру научного знания. Таков один из наиболее важных источников возрастания значимости процедур наблюдения в современной науке.

Итак, возникает такая несколько парадоксальная ситуация. Если объект повышенно ненаблюдаем нейтральным наблюдением и может наблюдаться только «активным» наблюдением (т.е. наблюдением, оказывающим существенное воздействие на существование объекта), то в этом случае процесс наблюдения оказывается не столько средством показать объект, не показывая наблюдение, сколько способом показать наблюдение, не показывая объекта. Объектом науки становится само наблюдение – вот хотя и несколько гиперболизированная, но как бы очищенная формулировка изменения статуса процесса наблюдения в современной квантовой физике и в определенной мере в современной философии науки. Эта формулировка повышает значение феноменализма в рамках научного принципа наблюдаемости (см. параграф «Наблюдение»), стремясь в большей мере ограничить сферу научного познания лишь областью инструментального наблюдения. В то же время следует отметить, что в современном научном познании средства научного наблюдения столь теоретически и технологически развиты, что современный феноменализм уже далеко отстоит от сферы наивного феноменализма, ограничивающего область научного познания только деятельностью внешних органов чувств человека.

§ 2. Принцип дополнительности

Еще одним активно обсуждаемым в современной науке принципом является так называемый «принцип дополнительности», также имеющим своим источником преимущественно квантовую физику. Создателем и наиболее ярким выразителем этого принципа был выдающийся датский физик, один из основоположников квантовой механики, Нильс Бор.

Микрообъекты – молекулы, атомы, элементарные частицы – обладают тем замечательным свойством, что не все характеризующие их величины можно одновременно и точно измерить (в отличие от объектов классической механики). Все параметры микрообъектов разбиваются на несколько классов (так называемых «полных наборов» величин). Одновременно и точно измеримы только величины из одного класса, одного полного набора. Что же касается величин разных полных наборов, то у микрообъекта эти величины можно одновременно определить только с некоторыми неопределенностями, отношение мер которых регулируется еще одним принципом квантовой механики - принципом неопределенности Гейзенберга. Смысл этого принципа в утверждении обратной зависимости мер неопределенностей свойств из разных наборов: чем меньше неопределенность измерения одной из двух величин разных полных наборов, тем больше неопределенность измерения другой величины, и наоборот. Величины разных полных наборов и получили название дополнительных величин (дополнительных свойств). Классическим примером дополнительных величин являются координата и импульс электрона. Чем точнее определяется положение электрона в пространстве, тем более неопределенным при измерениях оказывается импульс такого электрона, и наоборот. Принцип дополнительности представляет из себя описанную выше систему положений, определяющих отношения дополнительных свойств.

Нильс Бор высказал гипотезу, что дополнительные свойства могут встречаться и за пределами квантовой механики, например, в познании живых организмов. Бор предположил, что сложность построения теории живых организмов может быть связана, кроме всего прочего, с дополнительностью таких величин, как степень точности и «степень жизни» в познании живого объекта. Чем точнее мы пытаемся узнать строение и функционирование живого, тем более мы расчленяем целостный феномен жизни на отдельные элементы и тем самым теряем само свойство жизни. И наоборот – чем более живым является объект, тем более условием его живого бытия является целостность всех его частей, «растворяющая» и «маскирующая» в себе отдельные части. Подобная же логика дополнительности применима и к познанию процессов, протекающих в сознании.

Все свойства классического объекта могут быть представлены как свойства из одного полного набора, в то время как неклассические объекты могут обладать свойствами из нескольких полных наборов. В этом смысле неклассические объекты – микрообъекты, живые организмы, сознание – полнее классических объектов, соединяя в себе как бы несколько частных классических представлений. Неклассические объекты «больше» классических объектов, не умещаясь в отдельных «островах» свойств одного полного набора. Неклассическая наука 20-21-го века все более переходит к исследованию таких «больших сущностей», полнота проявления которых уже не умещается в одно из дополнительных классических представлений, и таких представлений требуется множество. Нужно множество дополнительных «классик» для выражения одной «не-классики».

§ 3. Принцип соответствия

Еще одним принципом, на формулировку и развитие которого оказала большое влияние современная физика, является так называемый «принцип соответствия». С накоплением точных и сменяющих себя во времени физических теорий, начиная с механики Ньютона и заканчивая современными физическими теориями (квантовая теория, теория относительности и т.д.), проявилась одна замечательная особенность в развитии теоретического знания. Оказалось, что более поздняя теория Т*, приходящая на смену более ранней теории Т, не просто отменяет действие теории Т, но находится с нею в некотором весьма своеобразном отношении, которое и было выражено специальным принципом – принципом соответствия. Что же это за отношение ?

Обычно ситуация складывается таким образом, что в более поздней теории Т* фигурирует некоторый характеристический для теории параметр р*. Например, это постоянная Планка h в квантовой механике или скорость света с в специальной теории относительности. Выразим ситуацию вхождения характеристического параметра р* в состав теории Т* в форме Т*(р*) – в виде зависимости теории Т* от р*. Параметр р* характеризует теорию Т* или как постоянная величина (константа), или как переменная величина, заданной в рамках некоторой области изменения Р*, характерной для Т*. В любом случае предполагается возможность такого представления теоретического знания Т*, в котором параметр р* будет представлен как переменная р, в связи с чем возникает и своего рода теория-переменная Т*(р), зависящая от переменной величины р. Переменная р предполагается заданной в рамках некоторой области определения Р, которая либо совпадает с областью Р*, либо включает ее в себя. Далее предполагается, что значение переменной величины р можно рассмотреть в некоторых точках р₀ области Р, получая частный случай теории Т*(р₀). Если, при всех вышеперечисленных условиях, для более ранней теории Т найдется такая точка р₀, что окажется выполненным равенство

Т*(р₀) = Т,

то говорят, что теория Т* находится в соответствии с теорией Т, или, что для теории Т* и Т выполнен принцип соответствия.

Приведенное выше равенство означает, что теория Т* может перейти в теорию Т при некотором значении характеристической переменной. Именно так оказываются связанными между собою более поздние и более ранние физические теории. Например, теория квантовой механики Q(h) и специальная теория относительности R(c), зависящие от параметров h и с соотв. переходят в классическую механику Ньютона N, если h устремить к нулю, а скорость света с – к бесконечности (теперь буквы «h» и «c» обозначают переменные). Эти условия символически можно было бы записать таким образом:

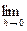Q(h) = N и 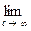R(c) = N

Здесь мы имеем дело с предельным соответствием, когда частные значения р₀ достигаются в качестве значений предельных стремлений переменной р. Такое предельное соответствие теорий может называться также аппроксимацией – теория Т* аппроксимирует теорию Т в предельном значении р₀.

Более простым примером использования принципа соответствия является, например, развитие идеи того или иного закона. Здесь Т* - более универсальная формулировка закона, Т – более частная. Например, вначале в истории физики был сформулирован закон Бойля-Мариотта, который утверждает обратную пропорциональность величин давления (р) и объема (V) газа: р = К/V, где К – какой-то коэффициент пропорциональности. Позднее этот закон обобщается в законе Менделеева-Клайперона: p = (mRT / M)/V . Здесь T - термодинамическая температура, m - масса газа, M - молярная масса, R - молярная газовая постоянная, причем второй закон переходит в первый, если предположить, что фиксированы масса и температура газа. Здесь в переходе от более универсального закона к более частному не используется предельный переход, но просто присваивается то или иное частное значение переменным, входящим в более универсальный закон. Кроме того, в этом примере мы видим, что в состав более позднего теоретического знания могут входить и более одного характеристических параметров (например, масса и температура в законе Менделеева-Клайперона).

Принцип соответствия является одним из важнейших принципов, регулирующих создание нового теоретического знания. В общем случае ученый стремится сформулировать такое знание Т*, которое бы находилось в отношении соответствия с уже принятым фрагментом теоретического знания Т. Поскольку не всякое возможное обобщение обладает свойством соответствия старому знанию, то принцип соответствия оказывается своего рода нетривиальным принципом отбора в развитии научного знания.

§ 4. Принцип симметрии

Развитие современной физики приводит к постоянному возрастанию роли разного рода симметрий и инвариантнов. Можно предполагать, что в дальнейшем эта тенденция будет только возрастать. Если во времена классической физики высшим уровнем научного познания был уровень наиболее универсальных законов, то с возникновением квантовой и релятивистской физики на первый план начинают выходить разного рода симметрии. Развитие физики происходит сегодня в направлении поиска и выражения все более глубоких и универсальных симметрий. Что же это за понятие – «симметрия»?

В современной физике и математике понятие симметрии обобщено до идеи инвариантности в некотором классе преобразований. Предполагается следующая система смыслов, связанная с такого рода трактовкой симметрии.

Когда говорят о симметрии, то как правило предполагают наличие некоторого класса преобразований Т, в которых объект О в том или ином смысле сохраняется (остается инвариантным). Объект О дан в виде своих состояний О_i, и когда трансформация Т переводит объект О из одного состояния O_i в другое его состояние O_j, т.е. Т(O_i) = O_j, то сам объект О остается в этом преобразовании неизменным: Т(О) = О. В этом случае говорят, что объект О симметричен (инвариантен) относительно преобразований Т. Класс всех тех преобразований Т, в котором объект сохраняется, характеризует симметрию объекта. Если, например, объект О* сохраняется в более обширном классе преобразований, чем объект О, то можно говорить, что О* более симметричен (инвариантен), чем объект О.

Рассмотрим такой простой пример. Допустим, на плоскости изображены квадрат и круг. Квадрат может быть совмещен с собою только при поворотах вокруг центра, кратных 90^о, в то время как круг совпадет с собою при поворотах на любой угол. С этой точки зрения круг оказывается симметричнее, чем квадрат.

Замечательно то, что геометрическая фигура (квадрат, круг и т.д.) – это не какое-то конкретное расположение фигуры в пространстве, но то нечто инвариантное (форма), что будет продолжать сохраняться во всех самосовмещающихся преобразованиях этой фигуры. При таком подходе фигура одновременно определена и как инвариантный объект О (форма), и как конкретные свои положения в пространстве О_i. Преобразования симметрии, например, повороты, сдвиги фигуры меняют только ее конкретные положения в пространстве (т.е. ее состояния О_i), но не меняют саму фигуру как инвариантный объект О (как форму). В то же время у всякого конечного объекта есть свой предел симметрии, за границами которого возникают преобразования Т* объекта О, меняющие его самого: Т*(О) ¹ О. Например, у фигуры можно изменить ее форму. Правда, в этом случае может быть определен более высокий уровень симметрии, с которым объект может быть отождествлен. Например, мы можем рассмотреть геометрическую фигуру не с точки зрения формы, а с точки зрения сохранения разрывов и связей ее точек. В этом случае, даже если мы будем деформировать фигуру, в то же время не делая в ней новых разрывов и склеек, мы не выйдем за границы этой более общей симметрии. Преобразования, сохраняющие разрывы и склейки, лежат в основании так называемых топологических симметрий.

Итак, симметрию можно изучать с точки зрения сохраняющих эту симметрию преобразований. Такие преобразования обладают так называемой «групповой» структурой. Группой в математике называют множество элементов с некоторой двуместной операцией о, где выполнены следующие три свойства:

1) ассоциативность: a о (b о c) = (a о b) о c для любых элементов a, b, c группы

2) существование нейтрального элемента группы e: a о e = e о a = a для любого элемента a

3) существование обратного элемента a^-1: a о a^-1 = a^-1 о a = e для любого элемента a

Например, множество целых чисел с операцией сложения + образует группу, нейтральным элементом в которой будет ноль, обратным элементом для числа k будет противоположное число (-k).

В случае разного рода симметрий структурой группы обладает множество тех преобразований, которые сохраняют симметрию объекта.

Симметрия может быть не только пространственной. Современная наука использует идею обобщенной симметрии в смысле описанной выше инвариантности объекта в соответствующих преобразованиях любой возможной природы. Например, объект, не изменяющийся во времени, будет обладать симметрией во времени. Женщина, теряющая со временем свою красоту, увы, не обладает такой симметрией. Современные женщины могут прилагать много усилий для сохранения или хотя бы имитации симметрии во времени. Герой Шварценегера из кинофильма «Хищник» выживает в страшных обстоятельствах борьбы с инопланетным монстром, в то время как все остальные участники операции погибают. Это тоже симметрия как высокая устойчивость и инвариантность в разного рода испытывающих обстоятельствах жизни. Нам нравятся люди, обладающие «жизненной симметрией», и мы сами хотели бы достичь подобной симметрии в своих сферах жизни. Разного рода процессы развития связаны с повышением симметрии и инвариантности. Например, в работах известного психолога Жана Пиаже представлены многочисленные экспериментальные и теоретические результаты его исследований развития интеллекта у детей. Главный вывод Пиаже состоит в том, что развитие интеллекта выражается в достижении все более обширных и глубоких симметрий интеллектуальных операций, в пределе образующих групповую структуру.

Таким образом, сегодня понятие симметрии оказывается все более актуальным и глубоким. Возрастает симметрия самого понимания симметрии, если так можно выразиться. Результатом этого процесса является формулировка принципа симметрии: в основе бытия лежат разного рода обобщенные симметрии. Познание этих симметрий – одна из важнейших задач современной науки.