Визначення прямокутних координат

ЛЕКЦІЯ 3.

РОЗВЯЗАННЯ ІНЖЕНЕРНИХ ЗАДАЧ ПО ТОПОГРАФІЧНИМ КАРТАМ ТА ПЛАНАМ

На попередніх лекціях ми розглядали питання створення топографічних карт та планів.

Зокрема розглянули як земна поверхня переноситься на площину способом ортогонального проектування; методику зменшення ділянок місцевості на картах та планах з використанням різних масштабів, як за допомогою номенклатури можна визначити положення листа карти чи плану на земній поверхні, використання умовних знаків для зображення на картах та планах ситуації та рельєфу місцевості, познайомились з поняттям сучасних цифрових та електронних карт, а також визначились з орієнтуванням як окремих ліній, так і планів та карт.

13. Читання топографічних карт та планів

Для комплексного розв’язання різноманітних завдань при вишукуваннях, проектуванні, зведені та експлуатації інженерних споруд треба вміти читати зміст топографічних карт та планів.

Зміст карт та планів зображений умовними знаками, які розкривають характер, смисловий зміст зображення об’єктів та рельєфу місцевості.

Читати карту означає вміння по умовним знакам зрозуміти, розпізнати і описати інформацію про ситуацію та рельєф місцевості, їх природні та технічні характеристики.

Для вирішення інженерних задач по картам та планам визначають:

- наявність геодезичних пунктів;

- характер рельєфу топографічної поверхні;

- гідрографію;

- рослинність;

- населені пункти, промислові, енергетичні та сільськогосподарські підприємства, аеродроми, порти, пристані і т.д.;

- наявність залізничних, автомобільних шляхів, покращених та ґрунтових доріг, нафто- та газопроводів, ліній зв’язку і т.і.

По характеру горизонталей, позначкам точок, характерним лініям рельєфу (вододілу та водозбору) визначають характер рельєфу земної поверхні (рівнинний, горбистий, пересічений, гірський), наявність скелястих обривів, промоїн, ярів, крутизну схилів і т.і.

При вивчені гідрографічних об’єктів (річок, озер, болот, струмків, каналів) звертають увагу на їх ширину, розмір, характер берегів, наявність переходів (мостів та бродів), глибину, швидкість течії і т.д.

Для визначення характеристик окремих об’єктів і явищ використовують пояснювальні умовні знаки:

- назви населених пунктів, річок, лісів, урочищ та інш.;

- скорочені написи характеру виробництва, матеріалу споруд, покриття доріг і т.д. розшифровують за допомогою умовних знаків;

- числові характеристики висоти, товщини дерев; довжини, ширини та вантажопідйомності мостів, ширини покриття доріг; напрям та швидкість течії води в річках і т.д.;

- знакові символи породи дерев у лісі, чагарників, лук, болота і т.д.

На основі проведеного камерального вивчення карти складають письмовий опис про ситуацію і рельєф місцевості, їхні природні та технічні характеристики.

Визначення довжин ліній

Геометричні параметри об’єктів місцевості можна визначати за допомогою чисельного, лінійного або поперечного масштабів карти та плану.

Довжина горизонтального прокладання лінії на місцевості визначиться за формулою

Д = d_пл · М. (3.1)

Довжину нахиленої лінії місцевості L визначають за формулою

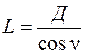, (3.2)

де n – кут нахилу місцевості .

Якщо виміряно горизонтальне прокладання Д лінії на місцевості, то її довжину на топографічному плані визначають за формулою

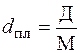. (3.3)

Довжину ламаної лінії (рис. 3.1) визначають як суму довжин окремих їх прямих ділянок за формулою

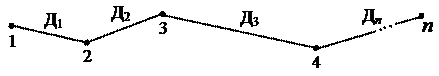Рис. 3.1. Вимірювання довжини ламаної лінії

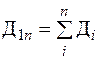. (3.5)

Вимірювання довжини хвилястої лінії виконується шляхом її поділу на приблизно прямолінійні відрізки. За допомогою вимірювача (рис. 3.2,а) послідовним відкладанням відрізків Д₀ визначають їх кількість п.

а

б

в

Рис. 3.2. Вимірювання довжини хвилястих ліній

а – за допомогою вимірювача; б – механічний курвіметр; в – електронні курвіметри

Довжину залишку DД визначають окремо. Тоді загальна довжина хвилястої лінії визначиться за формулою:

Д_АВ = п·Д₀ + DД , (3.6)

де Д₀ – визначена довжина прямолінійного відрізка.

При вимірюванні ліній великої довжини доцільно використовувати курвіметр (рис. 3.2,б,в).

Загальна довжина лінії визначиться за формулою

Д_АВ = (100×п + l) мм × М. (3.7)

Визначення прямокутних координат

Шукані прямокутні координати Х, Y точок визначаються відносно ліній координатної сітки (рис. 3.3).

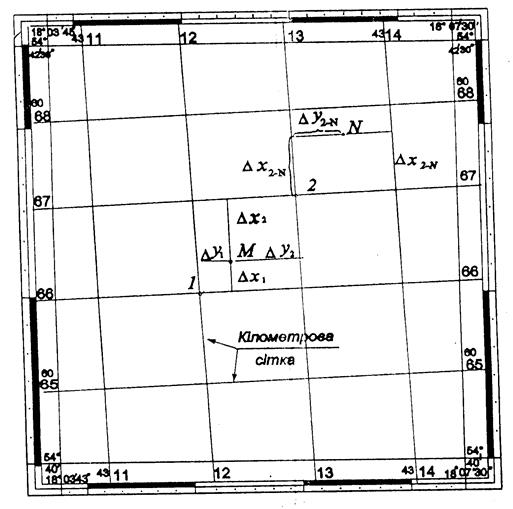Рис. 3.3. Визначення прямокутних координат точок на карті масштабу 1:10 000

Координати точок М і N визначають відносно координат південно-західного кута ліній квадрата координатної сітки (точки 1 та 2), в якому знаходиться шукана точка.

Прямокутні координати координат шуканих точок Х_j, Y_j обчислюють за формулами:

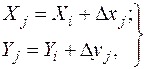, (3.8)

де Х_і, Y_i – координати південно-західного кута координатної сітки;

Dх_і, Dу_і – прирости координат шуканої точки відносно південно-західного кута.

Для точок М і N відповідно маємо:

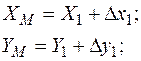
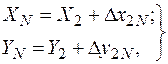. (3.9)

Приклад. При визначені координат точки М (рис. 3.3) без врахування деформації основи плану отримали Dх₁ = 280 м; Dу₁ = 400м. За формулою 3.9

Х₁ = 6066000 + 280 = 6066280 м.

Y₁ = 4312000 + 400 = 4312400 v/

Можна виконати обернену задачу – по заданим координатам точки N (X_N = 6067710м; Y_N = 4313520 м) нанести її на план масштабу 1:10 000 (рис. 3.3). Координати південно-західного кута координатної сітки – точки 2 дорівнюють:

Х₂ = 6067 км = 6067000 м; Y₂ = 4313 км = 4313000 м.

Відповідно Dх₂ = 6067710 – 6067000 = 710 м;

Dy₂ = 4313520 – 4313000 = 520 м.

У масштабі плану приріст абсциси Dх₂ = 710м і відкладаємо його по боковим лініям від південної сторони визначеного квадрата. Вподовж отриманої лінії від західної сторони лінії абсцис (Х) відкладаємо в масштабі плану приріст Dу = 520м і отримаємо положення точки N на плані.

16. Визначення дирекційних кутів та азимутів

Для вимірювання дирекційного кута лінії 1-2 (рис. 3.4) її продовжують вліво до перетину з лінією абсцис координатної сітки (точка 0).

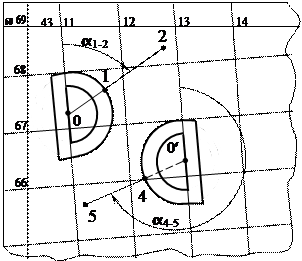Рис. 3.4. Вимірювання дирекційного кута

Величину дирекційного кута a_1-2 визначають за допомогою геодезичного транспортира (рис. 3.5). Точку 0 суміщають з центром дуги транспортира (нулем шкали на лінійці), а по краю лінії градусної шкали транспортира визначають величину кута a_1-2 .

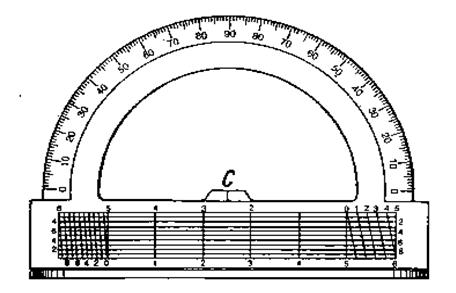Рис. 3.5 Геодезичний транспортир з поперечним масштабом

При вимірюванні істинного азимута заданої лінії користуються напрямом лінії східної або західної рамки карти, яка визначає напрям істинного меридіану.

Істинний азимут А за формулою

А = a + g, (3.11)

де g - Гауссове зближення меридіанів.

Відповідно можна обчислити магнітний азимут за формулами:

А_м = А - d; (3.12)

або А_м = a + g - d, (3.13)

де d – схилення магнітної стрілки.

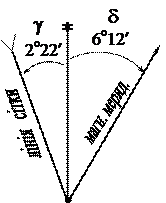Рис. 3.6. Графік розміщення орієнтирних меридіанів

Якщо визначити прямокутні координати кінцевих точок лінії X₁, Y₁; X₂, Y₂, то дирекційний кут a_1-2 можна аналітично обчислити за формулою

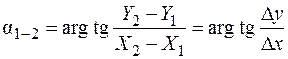, (3.12)

де Dх, Dу – приростки координат заданої лінії.

17. Розв’язання прямої та оберненої геодезичних задач

Пряма геодезична задача

Якщо відомі координати вихідної точки А(Х_А, Y_A), дирекційний кут лінії АВ (a_АВ) та довжина лінії d_АВ (рис. 3.7), то можна обчислити координати кінцевої точки В за формулами:

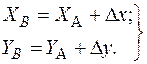. (3.15)

Прирости координат Dх та Dу згідно рис. 3.7 визначаються за формулами:

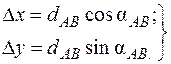. (3.16)

Рис. 3.7. Геометрична схема прямої та оберненої геодезичних задач

Приклад. Відомо Х_А = 6066275 м; Y_А = 43112398 м; a_АВ = 48^о15¢; d_АВ = 308,65 м. Визначити координати точки В. За формулами 3.15; 3.16 отримаємо:

Х_В = Х_А + d_АВcosa_АВ = 6066275 + 308,65 × cos 48^o15¢ = 6066534,9 м;

Y_В = Y_А + d_Аsina_АВ = 4312396 + 308,65 × sin 48^o15¢ = 4312626,3 м.