А) Монографии, учебники, статьи, рецензии 4 страница

Возвращаясь к мавандуйскому расположению триграмм (схема 18), следует отметить, что их внутреннее кольцо (НКРТМВД) получается тоже механически из внешнего (ВКРТМВД) по алгоритму (стрелки указывают порядок считывания триграмм внутри их пар, цифры — последовательность самих пар), основанному на структуре . Использование последней (для отбора нижних триграмм) в сочетании со считыванием по окружности триграмм внешнего кольца (для отбора верхних триграмм) представляет собой наглядный пример взаимодействия принципов цо и цзун, воплощенного также в ЛПТФС и ЛПТВВ (см. схему 19-21).

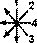
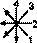
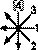
Структура определяет и алгоритмы получения из расположенной кольцом ВЛПТМВД всех связанных с действием цо последовательностей триграмм из «Шо гуа чжуани»: 1), 2), 5), 6) — соответственно 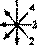. Эти алгоритмы показывают, что НКРТМВД (и соответственно НЛПТМВД) наиболее тесно взаимосвязано с последовательностями 2) и 6): с первой оно находится в отношении обратного считывания пар, со второй — сдвига на одну пару и их обратного считывания. В свою очередь последовательности 2) и 6) отличаются друг от друга сдвигом в считывании на одну пару. Обратность в считывании пар характерна для последовательностей 1) и 5). В целом данные структурные взаимозависимости свидетельствуют об уже отмеченной когерентности всех этих последовательностей.

Изящество структуры в сочетании с ее нумерологической осмысленностью, подтверждаемой внешними для нее данными (все ее стрелки в качестве алгоритма для считывания ВКРТМВД идут от мужских триграмм к женским в системе КРТВВ), говорит в пользу трактовки ВКРТМВД как исходной модели для 1), 2), 5), 6) последовательностей триграмм из «Шо гуа чжуани». Данное предположение может быть выдвинуто и в более развернутой формулировке: исходной моделью тут было КРТМВД, т.е. весь пространственно структурированный комплекс верхних и нижних триграмм, два главных компонента которого (ВКРТМВД и НКРТМВД) выводимы друг из друга. Принятие такой позиции находит основание в том, что все рассматриваемые последовательности триграмм — 1), 2), 5), 6) — получаются из НКРТМВД с помощью двух простых геометрических алгоритмов, представляющих собой симметричные сочетания трех и четырех петель (см. схемы 23-25).

Кроме того, одна из этих алгоритмических фигур 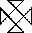(см. схемы 23-25), встречающаяся в Китае уже в росписях на древнейшей (баньпоской) керамике в виде 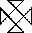и среди знаков древнейшей (иньской) эпиграфики в виде , является также алгоритмом преобразования КРТФС в ВКРТМВД и наоборот (см. схему 29). Настоящий алгоритм интересен своей 5-ричной формой (четыре треугольника вокруг квадрата), связывающей 8 или 9 (с центром) элементов. Связь 5 и 8 (9) — основа внутренней структуры Ло шу и Хэ ту, а также их и 8 триграмм внешней координации с 5 элементами. Возможно, вскрытый нами алгоритм является главным в системе взаимопреобразований пространственных расположений гуа. По-видимому, его исходная нумерологическая роль — преобразование обычной последовательности чисел 1...9 (в традиционной китайской записи сверху вниз и справа налево, заполняющей матрицу 3x3, см. схему 36а) в магический квадрат Ло шу (считывание схемы 36а по схеме 36б дает схему 36в, т.е. Ло шу). Следовательно, выяснение функции разбираемого геометрического алгоритма в структурных взаимосвязях мавандуйских расположений гуа с ранее известными расположениями (см. z:\CorvDoc\infopedia2\shchu01\txt02.htm - 23 схемы 23, 25, 29) подтверждает тезис традиционной китайской науки о производности порядков гуа от Ло шу. Наконец, считывание по НКРТМВД дает хорошую структурную интерпретацию двум усеченным (шестиэлементным) последовательностям 4) и 5), неполнота которых в этом случае выглядит алгоритмически обоснованной (см. схемы 26 и 27). Тут особенно стоит отметить, что алгоритм получения данной последовательности Вэнь-вана — 4) по НКРТМВД (схема 27) — своей формой схож с алгоритмом получения другой последовательности Вэнь-вана по КРТФС и ВКРТМВД (схемы 33 и 34).

Однако конкурентом ВКРТМВД в роли исходной модели продолжает оставаться КРТФС. Последовательности 1), 2), 5), 6) и НЛПТМВД считываются по нему с помощью алгоритмов, основанных на структуре 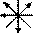(соответственно: ).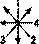

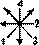
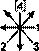
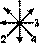
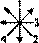Эта структура имеет свои преимущества. Во-первых, стрелки в ней не только идут от мужских триграмм к женским в системе КРТВВ, но и выделяют мужские триграммы именно в том порядке, в каком они сгруппированы в КРТВВ. Во-вторых, ее ось симметрии совпадает с линией деления КРТВВ на мужские и женские триграммы, что когерентно с первым пунктом. В-третьих, она тождественна структуре магического квадрата Ло шу (см. схему 28, где стрелки в Ло шу проведены от «формирующих» чисел — 6, 7, 8, 9 к «порождающим» — 1, 2, 3, 4), соотносимого с КРТВВ, что когерентно и с первым, и со вторым пунктом. По-видимому, смысл разбираемой структуры состоит в установлении определенной взаимосвязи между КРТФС, с которого по ней считываются триграммы, и КРТВВ, в соответствии с устройством которого таковые считываются.

Весьма вероятно, что эта связующая структура выведена из Ло шу (по схеме 28). Выделение в ней в качестве исходных для кодирования триграмм «формирующих» чисел 6, 7, 8, 9 вполне закономерно, поскольку таковые суть «четыре символа» (сы сян), обозначающие черты гуа и, как мы установили, отражающие геометрические формы восьми триграмм (см. схему 13). Если настоящее предположение верно, то прямой калькой с Ло шу следует считать последовательность 6), так как в ней перечисление пар триграмм при соотношении с числами Ло шу обнаруживает свое соответствие естественному счету в порядке от ян к инь: 9, 8, 7, 6. Такая моделирующая выделенность последовательности 6) подтверждается самим текстом «Шо гуа чжуани», где она фигурирует как главная классификационная схема, занимая наибольшее место (§7-11) и повторяясь пять раз, т.е. столько же, сколько все остальные последовательности вместе взятые[71]z:\CorvDoc\infopedia2\shchu01\refer.htm - s72. Последние и НЛПТМВД при аналогичном соотнесении с Ло шу также дают нумерологически осмысленный результат, образуя структурно целостную композицию:

1)	9 68 7	2)	8 76 9
НЛПТМВД	9 67 8	5)	7 86 9

Данный анализ свидетельствует в пользу традиционного нумерологического представления о генетической взаимосвязи Ло шу с системой триграмм, разделяемого и современными исследователями[72]z:\CorvDoc\infopedia2\shchu01\refer.htm - s73.

Структурный анализ пока не в силах окончательно решить проблему исторического приоритета, касающуюся двух исходных расположений триграмм: освященного нумерологической традицией, относимого к мифической древности КРТФС и созданного не позднее II в. до н.э., но забытого ВКРТМВД. Пока совершенно ясно, что все известные нам квадратно-круговые расположения триграмм структурно взаимосвязаны, т.е. преобразуемы друг в друга посредством простых, графически симметричных и нумерологически осмысленных алгоритмов. Все три таких алгоритма, связующих между собой КРТФС, ВКРТМВД и КРТВВ, представлены на схемах 29-31, демонстрирующих также сочетание принципов цо и цзун. Подобная взаимосвязь может быть истолкована как снимающее проблему исторического приоритета свидетельство одновременности возникновения рассматриваемых расположений триграмм.

В пользу такого предположения говорит и еще один факт, подтверждающий когерентность трех данных расположений: в них посредством группировки реализованы все три стандартных разделения триграмм на мужские и женские. Схемы 6 и 7 отражают соотношение соответствующих групп в КРТФС и КРТВВ. В ВКРТМВД (см. схему 18) наличествуют две перпендикулярные друг другу оси внутриструктурной симметрии (ср. структуру 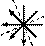и схему 21). Из них близкая к вертикали, как мы уже отмечали, разделяет мужские и женские триграммы согласно системе ЛПТВВ и КРТВВ, а близкая к горизонтали — согласно системе ЛПТФС. Следовательно, ВКРТМВД является своеобразным связующим звеном между «преднебесной» (Фу-си) и «посленебесной» (Вэнь-вана) системами, синтезируя в себе их принципы бинарной классификации триграмм.

Структурная взаимосвязь рассматриваемых квадратно-круговых расположений триграмм обнаруживается также с помощью ЛПТВВ. Эта последовательность была нами представлена в первом своем варианте, в котором главные, определяющие бинарную классификацию ее членов, триграммы Цянь и Кунь находятся вместе впереди, а за ними идут сначала три мужские триграммы Чжэнь, Кань, Гэнь, потом три женские — Сюнь, Ли, Дуй. Но существует и другой вариант данной последовательности полностью дихотомизированный (обозначим его индексом «Д» — ДЛПТВВ), в котором главные триграммы разделены друг с другом и поставлены впереди своих групп: Цянь, Чжэнь, Кань, Гэнь, Кунь, Сюнь, Ли, Дуй[73]z:\CorvDoc\infopedia2\shchu01\refer.htm - s74. Структурная двоичность ДЛПТВВ становится наглядно зримой при ее наложении на КРТВВ, образующем две перпендикулярные друг другу восьмеркообразные геометрические фигуры (схема 32). Наложение ДЛПТВВ на КРТФС и ВКРТМВД выявляет единую для этих расположений и также состоящую из восьмеркообразных петель фигуру (см. схемы 33 и 34). Наложение ДЛПТВВ на НКРТМВД, как и в случае с КРТВВ, видимо, подразумевающее представление данной последовательности в виде двух независимых рядов, порождает два квадрата, сдвинутых относительно друг друга на 45º (схема 35).

Анализ всех трех нумерологических фигур, полученных на схемах 33-35, выявляет любопытную закономерность: каждая из них представляет какую-то одну элементарную геометрическую форму — треугольник, ромб или квадрат (последние в свою очередь оказываются связанными с тремя различными числами — 4, 3 и 2, поскольку в соответствующих фигурах 4 треугольника, 3 ромба и 2 квадрата). Взглянув с этой точки зрения на схемы 29-31, также выражающие структурную взаимосвязь квадратно-круговых расположений триграмм, мы обнаружим сходную закономерность. Здесь тремя нумерологическими фигурами представлены три элементарных геометрических формы: треугольник, трапеция и квадрат (каждая в сочетании с двумя или четырьмя треугольниками).

В качестве общего вывода из проделанного анализа можно утверждать, что выявленные структурные взаимосвязи между пространственными расположениями триграмм демонстрируют лежащую в их основе комбинаторную систему элементарных геометрических форм. Последние, обретая статус нумерологических символов (сян), становятся методологическими универсалиями. Отсюда возникают, например, такие суждения: «Хозяйствующее над трудом — квадрат, хозяйствующее над управлением — круг» («Гуань-цзы», гл. 31)[74]z:\CorvDoc\infopedia2\shchu01\refer.htm - s75.

Наш более частный вывод — тезис о первичности квадратно-круговых расположений триграмм по отношению к их линейным последовательностям, которые являются различными видами их считывания, знаменуя собой определенные пространственные фигуры и алгоритмические переходы от одного построения к другому. Все отмеченные последовательности триграмм были рассмотрены в данном аспекте, поэтому более подробно проиллюстрируем наш тезис на примере лишь одной из них — ЛПТФС.

В ЛПТФС реализован принцип «Си цы чжуани» (I, 12): «Цянь и Кунь формируют ряд, и перемены устанавливаются внутри него»[75]z:\CorvDoc\infopedia2\shchu01\refer.htm - s76. Иными словами, в ЛПТФС триграммы Цянь и Кунь должны занимать крайние позиции: одна — в начале ряда, другая — в конце, остальные триграммы — между ними, т.е. внутри ряда. При таком условии считывание триграмм КРТФС простейшим способом — по окружности или периметру — осуществляется лишь в двух вариантах: 1. от Цянь до Чжэнь, от Чжэнь к Сюнь и далее до Кунь, 2. от Цянь до Гэнь, от Гэнь к Дуй и далее до Кунь. Второй из них ущербен, поскольку: а) не содержит никакой закономерности нарастания черт инь среди черт ян в триграммах, что задано самим условием движения от Цянь к Кунь, б) не согласуется с осью деления КРТФС на мужскую и женскую половину, отражающей хронотопографическую универсалию размежевания сфер ян (юг и восток, лето и весна — вверху и слева) и инь (север и запад, зима и осень — внизу и справа). В силу своей ущербности второй вариант отпадает, и остается только один — первый.

Следовательно, ЛПТФС, выражающая идею поступательного движения от ян к инь, или превращения одного в другое, и соответственно построенная по принципу закономерно-монотонного нарастания черт инь в перечисляемых триграммах и скоординированного с центральной осью считывания сначала всех мужских (ян), а затем всех женских (инь) триграмм, является автоматическим результатом приложения указанных концептуальных требований к КРТФС. Поэтому, кстати, нет никаких оснований видеть в ней запись особым двоичным кодом числового ряда 7...0 (см. схему 5 ) и отдавать ее автору приоритет в изобретении двоичного счисления[76]z:\CorvDoc\infopedia2\shchu01\refer.htm - s77.

Итак, известные нам линейные последовательности триграмм выводимы из их пространственных расположений, но не наоборот, что заставляет считать последние исходными. Роль же линейных последовательностей состоит не только во вторично-упрощенной фиксации соответствующих пространственных архетипов, но и, что, очевидно, важнее, в отражении их динамического аспекта, т.е. закономерностей превращения одной триграммы в другую в ходе универсального циклического процесса перемен (чжоу и).

Пространственные расположения и линейная последовательность гексаграмм, приписываемые Фу-си, построены по тому же принципу, что и соответствующие порядки триграмм (КРТФС, ЛПТФС). Некоторый нюанс тут вносит разделение квадратно-кругового расположения триграмм на два расположения гексаграмм — круговое (юань ту фан вэй) и квадратное (фан ту фан вэй). Первое представляет собой кольцо из 64 гексаграмм, в котором движение от Цянь к Кунь идет точно так же, как в КРТФС. Квадратное расположение, обычно помещаемое внутри кругового, представляет собой блок из 64 гексаграмм, образующих квадрат в 8 столбцов и 8 строк. Начальная гексаграмма Цянь здесь находится в северо-западном (нижнем правом) углу квадрата (а не на юге, вверху, как в круговом расположении), конечная гексаграмма Кунь — в юго-восточном (верхнем левом) углу (а не на севере, внизу). Движение от Цянь к Кунь, идентичное с таковым в кольце, идет в квадрате по строкам справа налево, снизу вверх. В целом эта система кругового и квадратного расположения самой своей формой выражает не только гармонию круглого неба и квадратной земли, но и равновесный характер космических процессов, состоящих из тождественных, но встречных потоков.

Данные принципы пространственного расположения распространяются и на порядок гексаграмм, приписываемый Вэнь-вану и реализованный в стандартном тексте «Чжоу и» в виде линейной последовательности. Ни формально-структурная, ни идейно-содержательная ее связь с ЛПТВВ и КРТВВ пока не прояснена. Не раскрыта до сих пор и общая внутренняя закономерность данной последовательности. Гексаграммы в ней располагаются парами: 28 пар построены по принципу обратности (фань), 4 (№1-2, 27-28, 29-30, 61-62) — по принципу супротивности (дуй). Последним восьми гексаграммам присуща центральная симметрия, они не изменяются при повороте на 180º, поэтому на них не распространяется принцип обратности. В силу такой внутренней организации последовательность Вэнь-вана может быть записана с помощью всего лишь 36 гексаграмм, если каждую из 28 пар, построенных по принципу фань, отражать одной гексаграммой, читаемой снизу вверх и сверху вниз[77]z:\CorvDoc\infopedia2\shchu01\refer.htm - s78.

В свою очередь, число 36 (6x6) находится в подозрительной близости к числу 6 как определяющему количественному показателю гексаграммы, происхождение и изначальный смысл которого пока не разгаданы. Нет однозначного ответа на вопрос, почему гуа образованы именно шестью, а не, к примеру, пятью или семью чертами. В этой связи интересна реанимация А.М.Карапетьянцем[78]z:\CorvDoc\infopedia2\shchu01\refer.htm - s79 раскритикованной Ю.К. Щуцким теории известного японского историка, академика Найтō Торадзирō (1866—1934), согласно которому исходные гуа состояли из пяти, а не шести черт и лишь впоследствии за счет добавления одной черты превратились из пентаграмм в гексаграммы[79]z:\CorvDoc\infopedia2\shchu01\refer.htm - s80. Гипотетическая пентаграммность исходных гуа привлекательна для объяснения их родства с архаической практикой гадания на панцирях черепах и лопаточных костях крупного рогатого скота, пятеричность которой подтверждается как нарративными источниками, так и данными археологии[80]z:\CorvDoc\infopedia2\shchu01\refer.htm - s81. Однако мотивы предполагаемого изменения этой системы, столь глубоко укорененной в традиции и столь удобной (соотнесенностью с естественным калькулятором — пятипалой рукой, членением пространства на четыре страны света и центр, пятью элементами и т.д.), все равно остаются затемненными.

Вероятно, изначальная или благоприобретенная гексаграммность гуа была обусловлена необходимостью получения соответствующего количества всех гексаграмм (64) или всех их черт (384). Особенно примечательно последнее число, равное максимальному количеству дней года в лунном календаре: 6 месяцев по 29 дней + 6 месяцев по 30 дней + 1 вставной (эмболисмический) месяц из 30 дней = 384 дня. В этом аспекте комплекс 64 гексаграмм предстает полной матрицей календарных символов годового цикла, который, кстати, мог обозначаться иероглифом чжоу, входящим в название «Чжоу и». И среди современных китайских специалистов пользуется успехом представление об астрономо-календарных истоках «Чжоу и»[81]z:\CorvDoc\infopedia2\shchu01\refer.htm - s82.

Исходя из того же фундаментального для памятника числа 384, можно предложить и более экстравагантную гипотезу, возвращающую к обсуждавшимся и отвергнутым Ю.К. Щуцким предположениям о некитайском происхождении «Чжоу и»[82]z:\CorvDoc\infopedia2\shchu01\refer.htm - s83. Как мы уже отмечали, продолжают оставаться необъясненными до конца терминологические обозначения иньских и янских черт иероглифами «шесть» и «девять». Если же мы проведем элементарную операцию сложения и установим общую сумму этих числовых значений всех 384 черт, то результатом будет весьма нетривиальное число 2880, как будто ничем не прославившееся в Китае, но зато игравшее важную роль в вавилонской вычислительной технике[83]z:\CorvDoc\infopedia2\shchu01\refer.htm - s84. В сочетании с целым рядом других подобных фактов (вроде использования 12- и 60-ричного циклов и т.п.), что Л.С.Васильев обобщает так: «Никто, по существу, никогда не оспаривал утверждений об аналогиях и даже заимствованиях древними китайцами западноазиатских представлений о небесной сфере и календарном исчислении. Сходство здесь слишком очевидно, чтобы его можно было всерьез ставить под сомнение»[84]z:\CorvDoc\infopedia2\shchu01\refer.htm - s85, — наше предположение о возможной закодированности вавилонского числа 2 880 в цифровых обозначениях черт китайской книги перестает казаться простой игрой ума.

Что же касается философского истолкования шестеричности гуа в самом тексте «Чжоу и», то в «Си цы чжуани» (II, 10) о ней говорится как о модели удвоения (видимо, по принципу инь — ян) «трех материй» (сань цай) — неба, человека и земли[85]z:\CorvDoc\infopedia2\shchu01\refer.htm - s86.

Спаривание гексаграмм в последовательности Вэнь-вана означает не что иное, как образование 12-членной матрицы, легко приложимой к календарно-хронологической сфере, прежде всего 12 месяцам года и 12 двухчасьям суток. С учетом отмеченной выше трехчастности каждой черты пара гексаграмм приобретает 36-членное строение, которое эффектно воспроизводится на более высоком уровне в комплекте из 36 гексаграмм, считываемых в обоих направлениях.

Основополагающий для попарной организации гексаграмм в «Чжоу и» принцип обратности (фань), в другой своей ипостаси являющийся законом дао — центрального предмета «Перемен как книги» («Си цы чжуань», II, 10)[86]z:\CorvDoc\infopedia2\shchu01\refer.htm - s87, возможно определил одну из таинственных особенностей последней, не раскрытую и Ю.К. Щуцким, в связи с чем его маститый рецензент вопрошал: «Осталось необъясненным, почему счет черт и объяснение их в гексаграммах идут не сверху, а снизу? Вопрос очень важный, не так ли?»[87]z:\CorvDoc\infopedia2\shchu01\refer.htm - s88.

Впрочем, эта важная особенность строения гексаграмм может быть понята и в свете еще одной фундаментальной идеи «Чжоу и»: «Порождение жизни (шэн шэн — варианты перевода: «оживотворение живого», «порождение порождающего». — А.К.) называется переменами» («Си цы чжуань», I, 5)[88]z:\CorvDoc\infopedia2\shchu01\refer.htm - s89. Если так определяется термин, вынесенный в само заглавие произведения, именуемого «Перемены», то вполне логично, чтобы его главные компоненты — гексаграммы, будучи визуальными образами, в своей образной форме и воспроизводили наиболее яркое проявление жизни — рост растений от земли к небу, т.е. снизу вверх.

Однако допустима и третья, чисто формальная причина. Как графический символ гексаграмма должна подчиняться общим принципам конструирования китайских топограмм, одним из которых является отождествление верха с передом, а низа с задом. Поэтому движение вперед тут автоматически становится перемещением снизу вверх. Иначе говоря, подъем в данной системе есть движение вперед, перенесенное из горизонтальной плоскости в вертикальную.

Итак, попарная сочетаемость гексаграмм в последовательности Вэнь-вана подчинена строгому алгоритму, что резко контрастирует с неясностью общего принципа соединения в ней самих этих пар. Вполне уместно прозвучало соответствующее замечание Ю.К. Щуцкому со стороны В.М. Алексеева: «А прослежена ли у Вас взаимозависимость гексаграмм? Связь одной гексаграммы с другой установлена, но вряд ли выдержана до конца и во всей ясности. Если ее нет, то, значит, и системы в «И цзине» также никакой нет»[89]z:\CorvDoc\infopedia2\shchu01\refer.htm - s90. В последнем тезисе В.М. Алексеев со свойственной ему страстностью, по-видимому, несколько перегнул палку, но в целом его упрек справедлив. В оправдание же Ю.К. Щуцкого следует сказать, что данная проблема чрезвычайно сложна и не решена до сих пор, хотя современные исследователи в ее решении могут использовать компьютерную технику. За последние годы у нас делались попытки приблизиться к разрешению этой загадки, в результате чего были выдвинуты некоторые оригинальные идеи и выявлен ряд отдельных характеристик последовательности Вэнь-вана[90]z:\CorvDoc\infopedia2\shchu01\refer.htm - s91. Эти пока еще предварительные достижения все-таки обнадеживают и внушают оптимизм относительно перспективы раскрытия системы «И цзина» в указанном В.М. Алексеевым смысле.

Вопреки иногда высказываемому мнению об отсутствии кругового расположения гексаграмм в порядке Вэнь-вана[91]z:\CorvDoc\infopedia2\shchu01\refer.htm - s92 таковое использовалось в китайской нумерологии[92]z:\CorvDoc\infopedia2\shchu01\refer.htm - s93, более того, по нашему мнению, является исходным для данного порядка. В круговом расположении Вэнь-вана начальные гексаграммы Цянь и Кунь находятся на севере, внизу, и движение от них идет по часовой стрелке, возвращаясь к исходному пункту. В квадратном расположении Вэнь-вана начальная точка помещена в юго-западном (верхнем правом) углу, конечная — в северо-восточном (нижнем левом), движение идет по строкам справа налево, сверху вниз. Следовательно, здесь, как и в расположении Фу-си, начальные точки кольца и квадрата, а также направления исходящих из них движений, взаимно противоположны. В свою очередь в том же отношении противоположности состоят друг с другом расположения Фу-си и Вэнь-вана, соотносимые с оппозицией цо — цзун и диаметрально отличающиеся своими начальными точками как в круговой, так и в квадратной форме. Все это наглядно демонстрирует универсальность общеметодологического принципа дополнительности противоположных начал (инь и ян), реализуемого на любом уровне мироописания.

Круговое расположение мавандуйского порядка гексаграмм подразумевается самим механизмом его порождения из КРТМВД и естественной аналогией со сходным образом порождаемым круговым расположением гексаграмм, приписываемым Фу-си. Мавандуйский текст «Чжоу и» написан на шелке, но он имитирует более древнюю форму записи на бамбуковых планках, разделяя иероглифы вертикальными линиями на узкие, в один знак, и длинные столбцы, в самом верху которых помещены гексаграммы[93]z:\CorvDoc\infopedia2\shchu01\refer.htm - s94. Ясно, что в такой записи на исходном материале — автономных бамбуковых планках — гексаграммы могли свободно раскладываться по кругу и вновь собираться в линейную последовательность. Эта замечательная по своей простоте возможность структурных трансформаций была с неизбежностью утрачена при переходе на другой писчий материал — шелк и бумагу.

Поскольку секрет расположения гексаграмм в порядке Вэнь-вана пока не раскрыт, закономерности его взаимосвязей с расположениями Фу-си и мавандуйским неясны. Два последних расположения, естественно, преобразуемы друг в друга по алгоритму, задаваемому соотношением соответствующих расположений триграмм. Гексаграммы обычно, как и в работе Ю.К. Щуцкого, указываются по их номерам в порядке Вэнь-вана. С помощью этих номеров мы воспроизведем здесь порядки Фу-си и мавандуйский, что, дополняя схемы 8, 9, 11, позволит в линейном аспекте представить соотношение всех трех последовательностей гексаграмм.

(1)	Последовательность Вэнь-вана:	1,	2,	3,	4,	5,	6,	7,
(2)	Последовательность Фу-си:	1,	43,	14,	34,	9,	5,	26,
(3)	Мавандуйская последовательность:	1,	12,	33,	10,	6,	13,	25,
(1)	8,	9,	10,	11,	12,	13,	14,						20,	21,	22,
(2)	11,	10,		38,	54,	61,	60,	41,	19,	13,	49,	30,	55,	37,	63,
(3)	44,	52,	26,	23,	41,	4,	22,	27,	18,	29,	5,	8,	39,	60,	63,
(1)	23,	24,	25,	26,	27,	28,	29,	30,	31,	32,	33,	34,	35,	36,	37,
(2)	22,	36,	25,	17,	21,	51,	42,	3,	27,	24,	44,	28,	50,	32,	57,
(3)	3,	48,	31,	34,	16,	62,	54,	40,	55,	32,	2,	11,	15,	19,	7,
(1)	38,	39,	40,	41,	42,	43,	44,	45,	46,	47,	48,	49,	50,	51,	52,
(2)	48,	18,	46,	6,	47,	64,	40,	59,	29,	4,	7,	33,	31,	56,	62,
(3)	36,	24,	46,	58,	43,	45,	31,	47,	49,	17,	28,	30,	14,	35,	56,
(1)	53,	54,	55,	56,	57,	58,	59,	60,	61,	62,	63,	64.
(2)	53,	39,	52,	15,	12,	45,	35,	16,	20,	8,	23,	2.
(3)	38,	64,	21,	50,	57,	9,	20,	53,	61,	59,	37,	42.