Часть 2. Методы и формы научного познания 4 страница

Но в любом случае традиция фундаментализма может быть представлена как убеждение в необходимости фиксации уровня некоторых неизменных оснований и осуществлении процедур обоснования только в связи с движением обоснования от этого фиксированного уровня по направлению ко всему остальному знанию.

На смену фундаментализму, по мнению З.А.Сокулер, с середины 20 века приходит в современную западную философию науки критическое отношение к любым процедурам обоснования. Такое настроение мысли мы будем вслед за З.А.Сокулер называть «антифундаментализмом». По мнению З.А.Сокулер, первым ударом по фундаментализму оказалась революция в физике конца 19 - начала 20 века, но «только кризис логического позитивизма привел к тому, что устои фундаментализма действительно зашатались. Чем далее, тем более очевидной становилась невозможность его защиты. В настоящее время мы являемся очевидцами становления новой – антифундаменталистской - парадигмы»[2]. Основополагающими в развитии антифундаментализма, по мнению З.А.Сокулер, оказались работы английского философа науки Карла Поппера и австрийского философа Людвига Витгенштейна.

Сходную точку зрения на развитие проблемы научной рациональности, если под рационализацией понимать разного рода процедуры обоснования, мы находим в работе «Наука и ценности»[3] американского философа науки Ларри Лаудана. В развитии западной философии науки в 20 веке Лаудан выделяет два основных этапа. Первый преимущественно пытался объяснить феномен удивительно распространенного в науке согласия (консенсуса) по основным проблемам научного познания. Возможность такого консенсуса связывалась философами, по мнению Лаудана, с существованием иерархической модели научной рациональности, включающей три уровня организации научного знания – фактуальный (включающий факты и научные теории), методологический (включающий разного рода методы научного познания) и аксиологический (ценностный, содержащий ценности, идеалы и нормы науки). Каждый последующий уровень выступает в этой модели как уровень оснований для предыдущего уровня. В конечном итоге последними основаниями научного знания выступают в этой модели аксиологические основания, и “поток” обоснования имеет здесь лишь единственное направление – от аксиологического через методологический к фактуальному уровню. Такого рода модель научной рациональности вполне соответствует идеологии фундаментализма. Итак, феномен научного консенсуса объяснялся философами в 30-50-х гг. нашего века приверженностью ученых идеологии фундаментализма. Во второй половине 20 века возникает “новая волна” философии науки, которая, по мнению Лаудана, делает акцент рассмотрения на возможности возникновения научных разногласий (диссенсуса) и подчеркивает иррациональные моменты научной деятельности. Диссенсус возникает в этом случае как результат невозможности определить те общие основания и акты обоснования, использованием которых ученые могли бы образовать возможность общего пространства решения тех или иных спорных проблем.

Таким образом, антифундаментализм утверждает, что не существует абсолютных оснований научного знания, все может быть подвергнуто критике. В то же время, как и фундаментализм, он не видит возможности построения иной модели обоснования знания, кроме той, которая была развита в фундаментализме. Антифундаментализм только утверждает невыполнимость этой идеальной модели в реальном знании. В этом смысле антифундаментализм еще лежит в той же плоскости, что и фундаментализм. Он принимает те же идеалы, что и фундаментализм, но, в отличие от последнего, антифундаментализм утверждает невыполнимость этих идеалов в реальности.

§ 4. Сетевая модель рациональности

В отличие от З.А.Сокулер, Лаудан не считает этап антифундаментализма последним шагом в развитии представлений о процедурах научного обоснования. Он выдвигает собственную, так называемую “сетевую”, модель научной рациональности, предполагающую возможность распространения процедур обоснования и на аксиологический уровень. Причем, это обоснование ценностей достигается не за счет восхождения к еще более иерархически высокому уровню научной рациональности, что было бы простым расширением иерархической модели научной рациональности. По мнению Лаудана, ценности научного познания, являясь основаниями для фактуального и методологического уровней, в свою очередь могут подвергаться критике и обоснованию с точки зрения этих уровней. Возникает феномен “взаимного обоснования”, когда обоснование “течет” в обе стороны. Лаудан пишет: “Сетевая модель очень сильно отличается от иерархической модели, так как показывает, что сложный процесс взаимного разбирательства и взаимного обоснования пронизывает все три уровня научных состояний. Обоснование течет как вверх, так и вниз по иерархии, связывая цели, методы и фактуальные утверждения. Не имеет смысла далее трактовать какой-либо один из этих уровней как более привилегированный или более фундаментальный, чем другие”[4].

Итак, существующий долгое время фундаментализм в проблеме обоснования научного знания сменяется во второй половине 20 века установкой антифундаментализма. Последний обнаруживает, что любые основания могут быть подвергнуты критике, т.е. в свою очередь могут быть подвергнуты процедурам обоснования. Но отсюда антифундаментализм делает вывод об отказе от процедур обоснования вообще, тем самым неявно солидаризируясь с фундаментализмом в принятии в качестве идеала обоснования фундаменталистского образа иерархической рациональности. И фундаментализм и антифундаментализм оказываются привержены одному и тому же идеалу обоснования научного знания, но второй лишь обнаруживает невозможность реализации этого идеала в реальности научного познания. Более радикальным – и потому не столь антипатическим – оказывается здесь подход Лаудана, изменяющего сам идеал научной рациональности, предлагающий рассмотреть вместо иерархической «сетевую» модель рациональности. В «сетевой» модели все основания теряют безусловный статус только оснований, все начала выступают и основаниями, и обосновываемым, возникает феномен «взаимного обоснования». Вместо образа антифундаментализма, столь ярко и безнадежно представленного К.Поппером в виде здания на сваях, вбитых в болото, возникает образ скорее сгустка живой массы, поддерживающего самого себя в невесомости и способного к росту в любом направлении. С этой точки зрения развитие представлений об основаниях знания вполне коррелирует с развитием представлений об основаниях устойчивости Земли – представления древних о плоской земной суше, покоящейся на надежном фундаменте трех слонов и черепахи (фундаментализм), вначале порождают сомнения в окончательной надежности самих опор (антифундаментализм), а затем претерпевают коренное преобразование в образе висящего в невесомости земного шара.

Научная рациональность оказывается более сложной, чем это казалось фундаментализму и антифундаментализму. Все начала, совокупно выстраивающие систему научного знания, могут выступать как в качестве оснований, так и в свою очередь подвергаться процедурам обоснования. Но нет ли в такого рода модели рациональности всем известной ошибки порочного круга (circulus vitiosus), когда А обосновывается через В, которое в свою очередь обосновывается через А? Как именно осуществляются процедуры «сетевого» обоснования, возможно ли в этом случае построение непротиворечивой модели такого рода обоснования?

§ 5. Метод последовательных приближений

Следует, во-первых, отметить, что в различных направлениях науки и научной методологии существует целый класс проблем, которые могут быть сформулированы как circulus vitiosus, но тем не менее зачастую не считаются ошибками. Такого рода проблемы можно называть «задачами круга». Например, В.Н.Садовский в работе «Основания общей теории систем»[5] приводит так называемый «парадокс целостности». Он пишет: «Решение задачи описания данной системы как некоторой целостности возможно лишь при наличии решения задачи «целостного» разбиения данной системы на части, а решение задачи «целостного» разбиения данной системы на части возможно лишь при наличии решения задачи описания данной системы как некоторой целостности»[6]. Подобным же образом в этой работе формулируются еще пять парадоксов, имеющих отношение к системному подходу. Их общую структуру автор резюмирует как логический круг: «В основе всех сформулированных парадоксов… лежит логический круг. В системных парадоксах выделяются две относительно самостоятельные задачи… и утверждается, что решение каждой из них зависит от предварительного решения другой задачи»[7].

Хорошо известен герменевтический круг, который можно рассмотреть как частный случай парадокса целостности в случае формирования процессов понимания. В словаре «Современная западная философия»[8], например, читаем: «Герменевтический круг – особенность процесса понимания, связанная с его циклическим характером. Герменевтический круг был известен уже античной риторике, а также патристике (для понимания Священного писания необходимо в него верить, но для веры необходимо его понимание - Августин). Различные модификации герменевтического круга связаны с осознанием взаимообусловленности объяснения и интерпретации, с одной стороны, и понимания – с другой; для того чтобы нечто понять, его необходимо объяснить, и наоборот. В герменевтике герменевтический круг разрабатывался как круг целого и части. В отчетливой форме представлен Ф.Шлейермахером (1768-1834): для понимания целого необходимо понять его отдельные части, но для понимания отдельных частей уже необходимо иметь представление о смысле целого (слово – часть относительно предложения, предложение – часть относительно текста, текст – часть относительно творческого наследия данного автора и т.д.). Шлейермахер выделяет психологическую сторону герменевтического круга: текст есть фрагмент целостной душевной жизни некоторой личности, и понимание «части» и «целого» здесь также взаимно опосредованы»[9].

Еще один пример “задач круга” – то, что можно назвать “генетическим кругом”. Обсуждая проблему взаимозависимости понятий времени, движения и скорости при развитии интеллекта ребенка, Дж.Флейвелл в работе “Генетическая психология Жана Пиаже”, например, пишет: “Анализ Пиаже показывает, что ситуация этого рода (т.е. взаимозависимость понятий – В.М.) возникает при генезисе интеллектуальных операций повсеместно: достижение представления А требует предварительного развития представлений В,С,Д и т.д., и наоборот, - нечто вроде генетического круга”[10].

А.И.Введенский в своей книге «Логика как часть теории познания»[11], касаясь ошибки порочного круга, пишет о том, что чаще всего она встречается в «длинных рассуждениях»[12]. Этому феномену можно найти объяснение в своего рода «парадоксе словаря»: для всякого понятия А найдется достаточно длинное определение, содержащее ссылку на А. Нечто подобное отмечает Л.Витгенштейн при описании структуры «языковых игр», утверждая: «И очевидной для меня делается не единичная аксиома, а система, в которой следствия и посылки взаимно поддерживают друг друга»[13].

Нечто похожее на «эпистемологический круг» можно найти в процессе познания, которое совершается не чисто дедуктивно или индуктивно, но идет «зигзагообразным путем», по выражению И.Лакатоса[14].

Подобные примеры можно продолжать бесконечно, но сам класс “задач круга” может быть достаточно ясно представлен, как нам кажется, уже на основе сказанного. Во всех “задачах круга” имеются, как минимум, два параметра А и В, каждый из которых может быть вполне определен только при условии предварительного определения другого параметра. В то же время от ошибки порочного круга “задачи круга” отличаются возможностью своего непротиворечивого решения. Многие из уже цитированных авторов предлагают одновременно метод такого разрешения “задач круга”.

Например, В.Н.Садовский пишет: “Выход из рассматриваемой парадоксальной ситуации… состоит в последовательных приближениях путем оперирования заведомо ограниченными и неадекватными представлениями”[15]. О подобном же методе пишет Дж.Флейвелл: «Хотя Пиаже не выражается на этот счет точно и четко, как хотелось бы, исходное предположение состоит в том, что указанный круг не превращается в порочный в силу того факта, что развитие происходит очень маленькими шажками: крошечное продвижение в одной области… прокладывает путь для столь же крошечного продвижения в другой; затем эти продвижения способствуют успехам в первой области, и таким образом движение по спирали продолжается на протяжении всего онтогенеза»[16]. В связи с такой структурой прохождения круга становится понятной «зигзагообразность» познания, о которой пишет И.Лакатос. Наконец, еще более детальное описание подобного метода мы находим у Р.Карнапа в «Философских основаниях физики»[17], который он также называет методом последовательных приближений. В примере, рассматриваемом Карнапом, речь идет о взаимоопределении величин температуры (Т) и длины (L). Чтобы определить длину, нужно учесть зависимость длины от температуры, т.е. предварительно нужно определить температуру. С другой стороны, определение температуры предполагает введение шкалы температур, которая предполагает уже определенной меру длины. Карнап пишет, что можно избежать порочного круга в этом случае следующим способом. Определим некоторую первоначальную шкалу длины, не учитывая ее зависимости от температуры. Это будет некоторая длина L₀. Она имеет определенную меру адекватности с точки зрения идеальной меры длины, что и оправдывает ее использование. На основе L₀ построим температурную шкалу Т₁. Теперь мы можем, отталкиваясь от Т₁, построить шкалу длины, учитывающую температуру по шкале Т₁, - это будет более инвариантная мера длины L₁. На основе L₁ можно построить T₂, и т.д. (см. [18]).

В описанном методе последовательных приближений вступает в отношение между собою некоторое множество начал, как минимум, множество двух начал А и В. Заметим, что для каждого из этих начал необходимо различать два уровня существования – некоторый интегральный уровень, на котором мы всегда будем иметь дело с двумя неизменными сущностями А и В (например, температурой (T) и длиной (L)), и уровень дифференциальный, на котором начала А и В будут изменяться и представать в виде своих «мод» А_i и В_i (например, таковы «модальности» температуры (T_i) и длины (L_i) в разобранном выше примере). Модальности А_i и В_i – это условные формы существования инвариантных начал А и В. Например, первая мода длины L₀ – это длина, определенная независимо от температуры, как бы при условии только самой себя. Если через символ А¯В обозначить определение А при условии предварительного определения В, то моду длины L₀ можно представить в форме L¯L - длина при условии самой себя. Первая мода температуры Т₁ образуется в этом случае как мода Т¯L₀ – температура, определенная при условии предварительного определения меры длины L₀. Далее мода длины L₁ возникает как мода L¯Т₁ – длина, определенная при условии предварительного определения меры температуры Т₁. Такое образование мод длины и температуры может продолжаться и далее.

Рассмотрим с точки зрения описанной структуры решение, например, проблемы герменевтического круга. Определим структуру текста в первом приближении как единство двух частей – начала Н и конца К. Тогда процесс понимания текста мог бы быть представлен, например, в следующем виде. Вначале читатель понимает начало текста, не зная конца. Обозначим такую степень понимания текста в виде Н₀. Затем, прочитывая конец, читатель понимает его, уже зная начало как Н₀ – так возникает вторая стадия понимания текста, которую можно обозначить как К₁ = К¯Н₀ – понимание конца при условии понимания начала как Н₀. После этого читатель может вновь обратиться к пониманию начала текста, но теперь это будет уже понимание начала при условии отмеченного выше состояния понимания конца: Н₁ = Н¯К₁. И такое понимание начала может быть неким иным состоянием понимание, сравнительно с Н₀. Продолжая так и далее, можно двигаться в некоторое «второе измерение» текста – измерение «глубины», в котором возможно не просто понимание той или иной части текста, но в связи со всеми остальными частями. Пределом такого движения окажутся некоторые такие степени взаимопонимания начала Н_n и конца К_n+1, что дальнейшие взаимоопределения уже не будут давать прироста нового смысла, т.е. H_n=H_n+1 и K_n+1 = K_n+2. Подобное положение дел можно рассмотреть как выражение состояния предельности метода последовательных приближений. Причем, в реальности такая величина n вполне может достигаться и на некотором конечном шаге, и даже, возможно, не слишком большом. Такие состояния взаимоопределения смыслов H_n и K_n+1 уже окажутся реальным вхождением в герменевтический круг их отношения. Но сам этот круг постепенно возникнет как предельный цикл спирального метода последовательных приближений, который и обеспечил возможность вхождения в круг (рис.2). Методы последовательных приближений составляют, по-видимому, существенный момент всякого процесса обоснования знания. В общем случае метод последовательных приближений на началах А₁, А₂, …, А_n выражается как бы во взаимном «притирании» этих начал через образование своих состояний с неограниченно возрастающей степенью взаимопроникновения. Здесь происходит все большее проникновение начал друг в друга, возрастание удельного веса определения начала с учетом предварительных определений других начал. Происходит как бы замыкание круга взаимных определений начал, они все более и более «притираются» друг к другу, в пределе образуя замкнутую в себе сферу, цикл взаимной поддержки и определения.

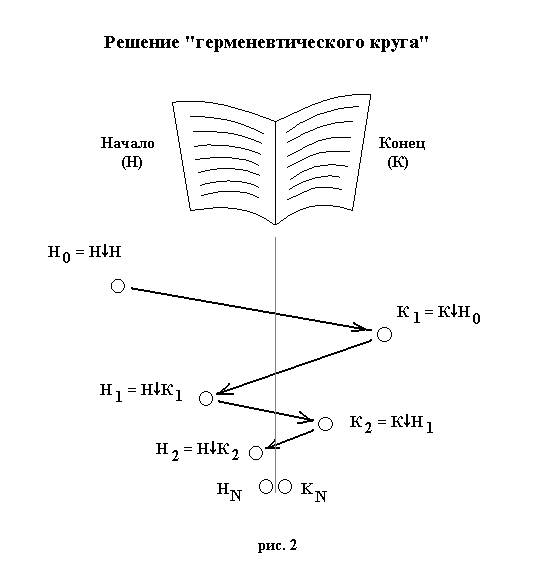
До этого момента движение метода последовательных приближений обходит цикл начал (хотя, возможно, и нерегулярно, не обязательно выдерживая порядок и направление обхода), но вновь образующиеся аспекты не повторяют предшествующих аспектов – возникает структура спирали, стремящейся уменьшить линейный компонент своего движения, замкнуть себя в предельном цикле.

Кроме процессов метода последовательных приближений на фиксированном множестве начал, в обосновании знания присутствует также момент добавления новых начал к уже имеющимся. В этом случае возникает необходимость как бы пере-сопряжения всего расширенного множества начал. Это, по-видимому, может осуществляться различными способами – сопряжением добавленных начал с системой уже ранее сопряженных начал, либо с предварительным «разрыхлением» ранее сопряженных начал и образованием новой системы сопряжения, включающей в себя как старые, так и новые элементы. Второй путь накладывает, по-видимому, ограничения на степень сопряжения первоначальных элементов – чем более система начал сопряжена внутри себя, тем, по-видимому, труднее этой системе вступить в новое сопряжение с внешними элементами. Отсюда оправданность хаоса в развитии знания – хаос может быть рассмотрен в этом случае как своего рода мера открытости («пластичности») системы, способности системы к расширению и росту. Таким образом, можно предполагать, что в процессах обоснования, предполагающих свое дальнейшее развертывание, сопряжение не доводится до конца, оставляя запас пластичности развивающейся системы. Тем не менее, в той или иной мере направление обоснования постоянно выражает себя в разворачивании процессов сопряжения на различных началах. В этом случае требуется относительная фиксация множества начал, вступивших в процесс сопряжения, своего рода относительное «замыкание» этого множества от внешних влияний. Таким образом, участки сопряжения образуют в процессе развития некоторые относительно полные и замкнутые системы начал, которые можно называть «плеронами» - единицами полноты в процессе развития. С этой точки зрения обоснование протекает в смене двух основных режимов – режима сопряжения начал в рамках того или иного плерона (момент эволюции в обосновании) и режима перехода от одного плерона развития к другому (момент скачка, революции в обосновании). Таким образом, обоснование разворачивается как бы ступенчато, двигаясь скачками от плерона к плерону и разворачивая согласования, сопряжения начал в рамках каждого плерона. Такого рода движение мы, по-видимому, находим в обосновании научного знания, в качестве начал в котором могут выступать эмпирические и теоретические уровни научного познания, различные понятия и теории, содержание и методы, методы и цели науки Во всех подобных процессах обоснования в качестве самостоятельного начала может оформиться в конечном итоге любая составляющая развивающейся системы, и вся система в целом всегда может вычленить в себе то или иное разбиение своих частей, всегда возможно – даже при фиксированной системе начал – изменение самих процедур взаимной детерминации. В конечном итоге процесс обоснования и развития знания приобретает гибкую и в то же время достаточно определенную структуру, существенно связанную с конструкциями процедур обоснования и метода последовательных приближений.

Глава 3. Наука и культура

§ 1. Определения культуры

Научная деятельность – это часть человеческой жизнедеятельности, наука – часть культуры. Понять науку во многом можно, только понимая культуру как человеческий способ бытия во Вселенной. В этой главе мы попытаемся посмотреть на научное знание и науку в целом как на одно из проявлений человеческой культуры. Для этого необходимо хотя бы в первом приближении разобраться, что вообще понимается под «культурой».

Существует множество различных определений культуры. Например, американский историк и антрополог Эдуард Тейлор определяет культуру как единство «из знания, верований, искусства, нравственности, законов, обычаев и некоторых других способностей и привычек, усвоенных человеком как членом общества»[19].

Западный историк и философ Й.Хейзинга в своей книге «Homo ludens» («Человек играющий») определяет культуру как игровое бытие, позволяющее человеку определять себя в форме различных игр. Жизнь в культуре – это всегда участие в той или иной человеческой игре, где присутствует момент соперничества, демонстрации, вызова, притворства, определены какие-то ограничительные правила, присутствует напряжение и непредсказуемость.

В работе «Философия символических форм» немецкого философа Эрнста Кассирера культура рассматривается как мир и движение различных символических форм, символов культуры. Мир символов помещается Кассирером между «реактивной» и «рецептивной» системами живого организма, образуя как бы новое измерение бытия. Язык, миф, искусство и религия образуют новую символическую реальность, в которой человек обитает как animal symbolicum – символическое животное, использующее и создающее символы.

В философии истории немецкого историка Оствальда Шпенглера культура рассматривается как живой исторический суперорганизм, обладающий своим временем рождения и жизненным циклом, завершающимся гибелью культуры. Культура живет – как на своем теле - на одном или нескольких народах. Каждая культура обладает своим высшим принципом («прасимволом»), который выражает себя в бесконечном разнообразии форм культурной жизни. Понять культуру – означает понять ее прасимвол, расшифровав все ее проявления как те или иные его проявления.

В психоаналитической традиции (Зигмунд Фрейд, Карл Юнг) культура определяется как система символов человеческого бессознательного, результат его «сублимации». Бессознательное не может прямо выразить себя в человеческом сознании и облекается в разного рода маскировки (символы бессознательного) – так рождается мир культуры.

Подобные примеры можно было бы продолжать до бесконечности, но, как нам представляется, во всех определениях культуры всегда присутствует некая общая идея, которая лишь по разному варьируется в разных определениях, подчеркивая те или иные стороны единого смысла понятия «культура».

Всеми определениями культуры так или иначе предполагается, что культура – это некоторое над-природное бытие человека. Человек живет в этом смысле в двух мирах – в мире природы, и в этой роли он подобен животным, и в мире культуры, который как бы надстраивается над природным миром, образует как бы 2-й этаж бытия, специфический именно для человека. С точки зрения природы (1-го этажа) мир культуры – это мир «символов», мир «игры», мир некоторых новых видов деятельности и способов быть, не встречающихся на 1-м этаже. В то же время со своей собственной точки зрения мир культуры – такой же самостоятельный мир, как и мир природы, со своими законами, ценностями, своим смыслом и целью.

Но культура – это 2-й этаж только относительно природы. Сама природа, однако, уже многоэтажна. Например, там есть этаж физического (неорганического) мира, а есть этаж мира органического. Органический мир – такой же новый уровень бытия относительно мира физического, как культура – новый этаж относительно всего природного мира. Если принять за точку отсчета мир неорганический, то понять культуру означает понять: 1) надфизическое бытие вообще, и 2) в частности, бытие человеческое. В движении к культуре от физики мы видим как бы два великих подъема – возникновение жизни и возникновение разума. Культура – это и есть такая дважды приподнятая физика. Именно поэтому культуру и ее формы (например, науку) трудно понять, поскольку до сих пор мы лучше всего научились понимать только мир неорганических тел.

§ 2. Культура как онтология

Итак, культура – это особый мир, надстоящий над миром физическим. В философии для обозначения той или иной реальности, возможного мира часто используется слово «онтология». В классическом употреблении слово «онтология» происходит от двух греческих слов: «онтос» - сущее, то, что есть на самом деле, что реально существует; и «логос» - учение. В целом, «онтология» - учение о сущем, о том, что реально существует. Таким образом, под «онтологией» обычно подразумевался такой раздел философии, где изучается мир как объективная реальность, независящая от нашего произвола. Это своего рода «философская физика», занимающаяся исследованием вопросов о бытии (существовании), пространстве и времени, причинности, и т.д. Однако в последнее время, в 20-21 веках, в современной философии слово «онтология» все чаще стало использоваться в несколько ином смысле. Под «онтологией» стали понимать любой возможный мир, возможную реальность со своим пространством-временем, своей материальностью, системой законов и ценностей и т.д. В этом смысле и мы далее будем употреблять термин «онтология».

Каждая онтология, каждый возможный мир должен обладать некоторыми необходимыми составляющими. Например, чтобы автомобиль работал, нужно, чтобы все детали были на месте и правильно взаимодействовали друг с другом. Точно так же, чтобы начал существовать некоторый мир, нужно, чтобы в нем было то, где что-то происходит, чтобы оно когда-то происходило, чтобы что-то и как-то происходило. Поэтому можно предполагать с большой долей уверенности, что каждая онтология – это единство, по крайней мере, своих:

- пространства

- времени

- материальности

- сущностей

- законов

- смыслов и целей …

Онтология – это не обязательно физический мир, который мы считаем существующим. Онтология – это любой возможный мир, в том числе и то, что сегодня называется «виртуальной реальностью». Это может быть:

- «онтология сна»

- «онтология романа»

- «онтология компьютерной игры»

- «онтология игры»

- «онтология культуры»

- «онтология науки»

Главное, чтобы это была некоторая возможная реальность со своим пространством-временем, своими сущностями, законами, и т.д., образующая относительно замкнутый «малый мир». Например, в онтологиях компьютерных игр могут быть какие угодно пространства и времена - конечные или бесконечные, плоские или объемные, одно- или многоуровневые, какие-угодно сущности – монстры, герои, живые камни, поющие облака, собственные правила игры-жизни и свои ценности, и т.д. То же относится к онтологиям литературных произведений – это и Миры Толкиена, и Миры Желязны, Роулинг, Миры Достоевского и Кафки, «Облако в штанах» Маяковского или живой океан Солярис у Станислава Лема, и прочее, и прочее… Примерам несть числа.

Новизна «онтологического» подхода к разным фрагментам реальности состоит в рассмотрении этих фрагментов как малых миров, малых Вселенных. Это, по-видимому, дух нашего времени, в котором все более нарастает философия самоподобия – когда части целого подобны в той или иной мере самому целому. Так в современной философии нарастает интерес к таким сущностям или к таким способам рассмотрения сущностей, когда они представляются как малые миры – онтологии. Например, одно из влиятельных направлений философии 20-го века – экзистенциализм, попытался рассматривать мир человека как онтологию, как свою самостоятельную вселенную. До этого человеческие способы жизни рассматривали психологически, а не онтологически, т.е. не как самостоятельное бытие, но как некоторое слабый, иллюзорный способ существования, по большому счету в таком виде и не существующий. Онтологизация при изучении той или иной реальности выражается, по-видимому, в первую очередь в том, что эту реальность не пытаются сводить ни к какой другой реальности, но рассматривают ее как таковую, как отдельный и самостоятельный способ бытия в мире. Например, ту же реальность компьютерной игры можно рассмотреть двояко: 1) как это делает программист, когда он сводит реальность игры к некоторой другой реальности – к реальности программ и их технического обеспечения. Он будет думать не столько о том, что герой станет делать, встретившись с врагом, сколько о том, как это будет выглядеть в форме алгоритмов и программных команд. 2) и можно воспринимать игру «изнутри», как это делает ее пользователь, ее игрок. В этом случае игра и определяет себя как онтология, как возможный мир, который переживается и пропускается сквозь себя ее участником.