Примеры программ в стиле SPMD и MPMD
При программировании для сетевых кластеров используется SPMD-технология (SingleProgram – MultipleData, одна программа – множественные данные). Идея SPMD в том, чтобы поделить большой массив информации между одинаковыми процессами, которые будут вести обработку своей части данных. В случае SPMD-подхода достаточно рассылать время от времени процессам блоки данных, которые требуют трудоемкой обработки, а затем собирать результаты их работы. Если время обработки блока данных одной машиной значительно больше, чем время пересылки этого блока по сети, то сетевая кластерная система становится очень эффективной.
Именно такой подход используется в MPI. Здесь всегда есть основной процесс, который производит распределение данных по другим машинам, а после окончания вычислений собирает результаты и показывает их пользователю. Обычно процесс-мастер после распределения данных также выполняет обработку их части, чтобы использовать ресурсы системы наиболее эффективно.
Пример программы в стиле SPMD
ProgramExample3d
Implicit None
Include 'mpif.h'
Integer Size, Rank, Ierr, I, N
Double Precision Sum, GSum, A, B, time1, time2, Al, Bl, X, F
! Пределы интегрирования
Parameter (A=0.d0, B=1.d0)
! Подынтегральная функция
F(x)=DLog(1/x)
Call MPI_INIT(Ierr)
Call MPI_COMM_SIZE(MPI_COMM_WORLD, Size, Ierr)
Call MPI_COMM_RANK(MPI_COMM_WORLD, Rank, Ierr)
! «0»-процессзасекаетвремя
If (Rank.eq.0) time1 = MPI_WTime()
! Каждый процесс определяет свои пределы интегрирования
! и число интервалов разбиения
Al = A+(B-A)*Rank/Size
Bl = Al+(B-A)/Size
N = 1000000
! Каждый процесс определяет свою частичную сумму
Sum = 0
Do I = 1,N
X = Al+(Bl-Al)*(I-0.5d0)/N
Sum = Sum + F(X)
End Do
! «0»-процесс получает результат суммирования частичных сумм
Call MPI_REDUCE(Sum, GSum, 1, MPI_DOUBLE_PRECISION, MPI_SUM, 0, MPI_COMM_WORLD, Ierr)
If (Rank.eq.0) Then
time2 = MPI_WTime()
GSum = GSum/(N*Size)
Write (6,*) 'Result=',GSum,' Error=',1-GSum, ' Time=',time2 - time1
End If
Call MPI_FINALIZE(Ierr)
Stop
EndProgram
3.Напишите программу параллельного вычисления определенного интеграла от фукнции 2*sin(x) в интервале [0,1].
double f(double x)
{return 2*sin(x);}
int main(intargc,char **argv)
{
intsize,rank;
MPI_Status status;
MPI_Init(&argc,&argv);
MPI_Comm_rank(MPI_COMM_WORLD,&rank);
MPI_Comm_size(MPI_COMM_WORLD,&size);
float h=0.05,a=0,b=1,s=0.0;
for(inti=rank; a+h*(i+1)<b+h; i+=size)
{ s+=h*f(a+h*(i+1)); }
if(rank!=0)
{ MPI_Send(&s,1,MPI_FLOAT,0,1,MPI_COMM_WORLD); }
if(rank==0)
{ float r;
MPI_Recv(&r,1,MPI_FLOAT,1,1,MPI_COMM_WORLD,&status);
s+=r;
printf("s=%f\n ",s);
}
}
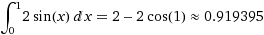
Сурак
1.В каких случаях эффективно использование параллельных методик программирования ?
В последнее время, чтобы получить возможность задействовать на практике ту дополнительную вычислительную мощность, стало необходимо задействовать параллельные вычисления. Сейчас по разным причинам производители процессоров предпочитают многоядерные архитектуры, и для получения всей выгоды от возросшей производительности ЦП программы должны переписываться в соответствующей манере. В итоге происходит неуклонное возрастание потребности в ресурсоемкихрасчетах, которые в ряде случаев можно выполнить только на базе высокопроизводительной техники с помощью методов параллельных вычислений. Параллельные вычисления применяются в:
1) системах поддержки проектирования (CAD – ComputerAidedDesign). В таких системах необходимость осуществлять моделирование в реальном масштабе времени предъявляет высокие требования к производительности программного обеспечения. 2) инженерных приложениях. К этому классу относятся разнообразные задачи из области прочностного моделирования, моделирование аварийных ситуаций и многие другие; 3) математическом моделировании физических процессов. В этот широкий класс входят задачи динамики жидкости и газа, электромагнитные и ядерные взаимодействия, процессы горения и т.п. Такие процессы, как правило, описываются системами уравнений в частных производных. 4) моделирование глобальных процессов в науках о Земле. В первую очередь, это – задачи прогноза изменения климата, предсказание природных катаклизмов. 5) вычислительной химии. Разнообразные задачи этой области направлены на изучение свойств вещества в различных состояниях. 6) бизнес-приложениях. К этой категории относятся задачи, связанные с анализом финансовых рынков и прогнозирования курсов валют. Также распространены оптимизационные задачи, по формированию наилучшего варианта использования финансовых или иных ресурсов, построения оптимальных транспортных и телекоммуникационных сетей, размещения предприятий в регионе и многие другие задачи.
