VIII. Косинус угла между двумя векторами
Тема 9. Действия с координатами вектора
I. Равенство векторов
Если соответствующие координаты двух векторов равны, то равны и сами векторы.
Задача 1.Определить, какие из векторов равны 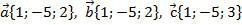
Решение:
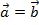 - так как их координаты равны;
- так как их координаты равны;
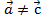 - так как их координаты не равны;
- так как их координаты не равны;
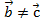 - так как их координаты не равны.
- так как их координаты не равны.
II. Координаты вектора
Задача 2. Найти координаты вектора, заданного координатами начальной и конечной точки 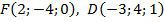 .
.
Решение:
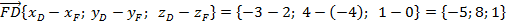 .
.
Ответ: 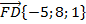
III. Длина вектора (или модуль вектора)
Рассмотрим вектор на плоскости и в пространстве. При параллельном переносе проекций вектора к начальной и конечной точкам вектора, получим прямоугольный треугольник, в котором гипотенузой является сам вектор. Поэтому длину вектора находим по теореме Пифагора 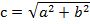 или или 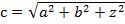 Длина вектора, заданного координатами точек начала и конца На плоскости: Длина вектора, заданного координатами точек начала и конца На плоскости: 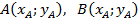 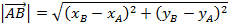 В пространстве: В пространстве: 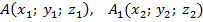 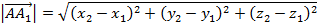 Длина вектора, заданного своими координатами На плоскости: Длина вектора, заданного своими координатами На плоскости: 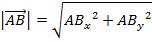 В пространстве: В пространстве: 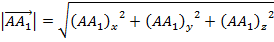 | 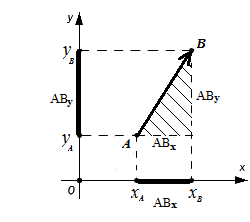 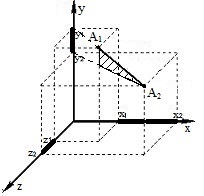 |
Примеры нахождения длины вектора (по координатам точек и по координатам вектора)
Задача 3. Найти длину вектора, заданного координатами точек 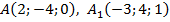
Длина вектора
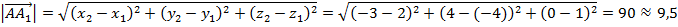
Задача 4. Найти длину вектора, заданного своими координатами 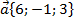 , где
, где 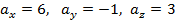
Длина вектора 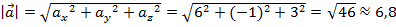
IV. Сложение (вычитание) векторов
Результатом суммы (разности) векторов 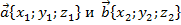 является вектор, координаты которого получены путём сложения (вычитания) соответствующих координат векторов
является вектор, координаты которого получены путём сложения (вычитания) соответствующих координат векторов 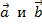
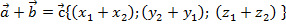
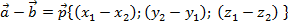
Примеры сложения (вычитания) векторов
Задача 5.Найти сумму и разность векторов 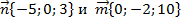
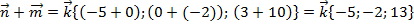
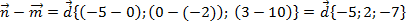
V. Произведение вектора на число
Результатом произведения вектора 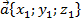 на число
на число 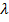 является вектор, координаты которого получены путём умножения на число
является вектор, координаты которого получены путём умножения на число 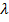 каждой координаты исходного вектора
каждой координаты исходного вектора
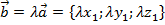
Векторы 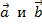 при этом являются коллинеарными. Поэтому данное действие даёт возможность проверить коллинеарны векторы или нет.
при этом являются коллинеарными. Поэтому данное действие даёт возможность проверить коллинеарны векторы или нет.
Пример умножения вектора на число
Задача 6.Найти произведение вектора 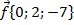 на число
на число 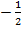
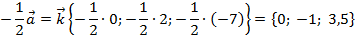
VI. Коллинеарность векторов
Два вектора коллинеарны, если их соответствующие координаты кратны одному и тому же числу.
Пример проверки коллинеарности векторов
Задача 7.Проверить коллинеарность векторов 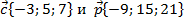
Векторы 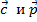 коллинеарны, так как
коллинеарны, так как 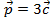
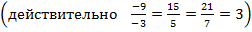
VII. Скалярное произведение векторов
Скалярным произведением векторов 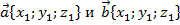 является число, равное сумме произведений соответствующих координат
является число, равное сумме произведений соответствующих координат
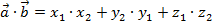
Если скалярное произведение векторов равно нулю, то векторы ортогональны.
Пример выполнения скалярного произведения векторов и проверка ортогональности
Задача 8. Найти скалярное произведения векторов 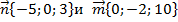
Решение: 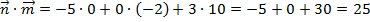
Задача 9. Проверить ортогональность векторов 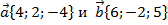
Решение: 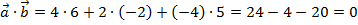 , следовательно
, следовательно 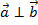 .
.
VIII. Косинус угла между двумя векторами
Косинус угла между двумя векторами равен отношению скалярного произведения векторов на их длины.

Если 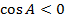 , то угол между векторами
, то угол между векторами 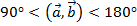 (т.е. угол тупой).
(т.е. угол тупой).
Если 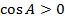 , то угол между векторами
, то угол между векторами 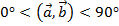 (т.е. угол острый).
(т.е. угол острый).
Если 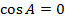 , то угол между векторами
, то угол между векторами 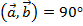 (т.е.
(т.е. 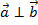 ).
).
Это возможно лишь при 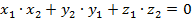 (свойство ортогональности).
(свойство ортогональности).
Данное свойство позволяет устанавливать перпендикулярность не только векторов, но и прямых, на которых лежат векторы. В том числе перпендикулярность прямых в пространстве, т.е. скрещивающихся прямых.
Пример определения косинуса угла между векторами
Задача 10.Определить 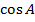 в
в 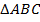 , если даны координаты его вершин:
, если даны координаты его вершин: 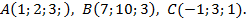
Решение: каждый из трёх углов треугольника образуется двумя векторами:
-угол А: векторами 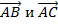
-угол B: векторами 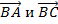
-угол C: векторами 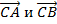
Тогда косинус угла находим по формуле

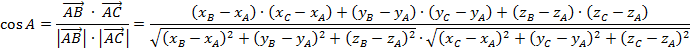
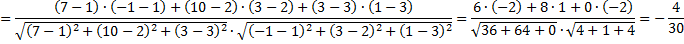
После сокращения получаем: 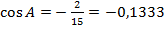 .
.
Ответ: 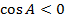 , значит
, значит 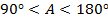 т.е.
т.е. 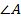 тупой.
тупой.
Формулы для определения 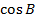 и
и 
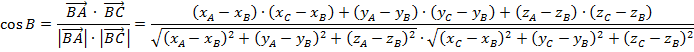
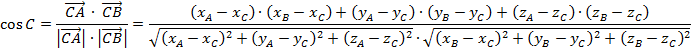
Контрольное задание №9 по теме
«Действия с координатами вектора»
Задача 1.Определить, какие из векторов равны 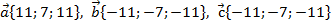
Задача 2. Найти координаты вектора 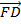 , заданного координатами точек
, заданного координатами точек 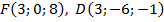 .
.
Задача 3. Найти длину вектора 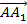 , заданного координатами точек
, заданного координатами точек 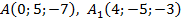
Задача 4. Найти длину вектора, заданного своими координатами 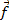 , где
, где 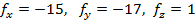
Задача 5.Найти сумму и разность векторов 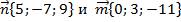
Задача 6.Найти произведение вектора 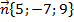 на число
на число 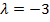
Задача 7.Найти скалярное произведения векторов 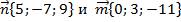
Задача 8. Подберите координаты вектора 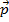 так, чтобы
так, чтобы 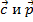 были коллинеарны
были коллинеарны 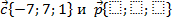 .
.
Задача 9. Подберите координаты вектора 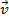 так, чтобы
так, чтобы 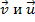 были ортогональны
были ортогональны 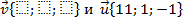
Задача 10.Определить 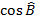 в треугольнике
в треугольнике 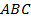 , если даны координаты его вершин:
, если даны координаты его вершин:
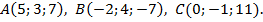 Сравните значение
Сравните значение 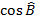 с нулём и определите, острый угол или тупой.
с нулём и определите, острый угол или тупой.
