Глава 3. Прояснение смысла. Законы Ньютона.
В1663 году, спустя 33 года после публикации «Двух новых наук» Галилея, молодой выпускник колледжа Святой Троицы в Кэмбридже сидел в своём доме, в деревне графства Линкольншир, и заканчивал построение «обширной и великолепной науки» Галилея (механики). Изгнанный эпидемией Великой Чумы из университетского Кэмбриджа, Исаак Ньютон плодотворно использовал период своей вынужденной изоляции от того интеллектуального окружения, к которому привык в Кэмбридже. Он вернулся в своё малое владение, где был рождён 23 года назад.
Сравнение Галилея и Ньютона позволяет подметить интересные контрасты. Трудно представить что-либо более несхожее, чем светскость и заносчивость Галилея и вежливая, почти мистическая сдержанность Ньютона. Галилей полагался только на себя и любил публичную полемику. Ньютон же был унылым интровертом и оставлял друзьям право вести борьбу за него. Если Галилей мог спрятать свой скептицизм за формальной капитуляцией перед Инквизицией, чтобы не «грузить» понапрасну своё сознание, то Ньютон на протяжении всей жизни оставался убеждённым, если не фанатичным, христианином.
Семья Галилея надеялась, что его занятия помогут вернуть ей высокий статус, в то время как родители Ньютона готовы были видеть в нём такого же, как они, простого фермера.
Однако юный Исаак фермерским обязанностям предпочитал чтение, и поэтому семья решила послать его в Кэмбридж, где уже получили образование несколько его родственников. Прибыв туда, он обнаружил, что годы гражданской войны оставили университет еле живым, физически и интеллектуально. Немногие из профессоров могли предложить что-то интеллектуально привлекательное. Кроме того, в отличие от знаменитых итальянских университетов, в Кэмбридже мало занимались натуральной философией, которая представляла главный интерес для Ньютона. Кафедру натуральной философии возглавлял Исаак Барроу, математик-любитель, у которого первой любовью была теология. Барроу не имел иллюзий в отношении собственной квалификации. Он опекал Ньютона, как только мог, и позже по собственному желанию покинул свой пост, как только Ньютон достиг 26 лет, позволявших ему занять кафедру.
Даже для такого естественного затворника, как Ньютон, изоляция Кэмбриджа от основного научного мира была почти непереносимой. Он лучше чувствовал себя в Лондоне, среди своих товарищей, страстно преданных науке, таких как астроном Эдмунд Галлей, архитектор Кристофер Рен, философ Джон Локк, а также соперник Ньютона физик Роберт Гук.
Члены этого круга считали, что в мире нет места сверхъестественному и нет пределов мощи Разума при разгадывании мистерии Вселенной. Они считали, что Бог мог создать законы природы при её сотворении, но он не вмешивается в ежедневные дела своего мира. Они не верили философии Декарта, которая казалась им попыткой создать новую схоластику в одеянии науки для того, чтобы утвердить интеллектуальный авторитет Римской церкви. Все они видели в Ньютоне потенциального лидера, который мог разгромить картезианцев на их собственном поле.
Ньютон не испытывал интереса к такой борьбе. Он был болезненно чувствителен к малейшей критике в свой адрес. Потребовалась вся сила убеждения Галлея, чтобы упросить его завершить величайший труд «Математических начал натуральной философии» (обычно именуемый как «Принципы»), и опубликовать его в 1686 году.
Законы Ньютона.
Полная теория механического движения Ньютона оказалась настолько совершенной, что сохранилась практически в первоначальной форме до наших дней. Она базируется на двух ключевых прозрениях.
1. Центральной проблемой механики является изменение состояния движения, т.е. отклонение от поведения, описанного в принципе инерции.
2. Такое отклонение происходит только при взаимодействии двух объектов, в результате которого изменяется движение обоих объектов.
Чтобы рассмотреть проблему количественно, Ньютону понадобились три понятия – ускорение, сила и масса. Ускорение, первоначально определённое Галилеем, он рассматривал как количественную меру быстроты изменения состояния движения. Сила, как мера способности окружения вызывать это изменение, была понятием, уже широко известным во времена Ньютона. Масса, как показатель способности тела сопротивляться изменению его состояния, была в большой степени собственным изобретением Ньютона. В действительности, он рассматривал массу как истинную меру «количества материи» в теле. В этом смысле масса подобна значению слова вес. Различие между весом и массой будет обсуждаться в этой главе позже.
Ньютон использовал импульс в понимании Гюйгенса, как истинную меру движения, заменив вес массой при его определении. Он также добавил схему взаимодействия тел, при которой передача импульса от одного тела другому происходит непрерывно, а не в процессе только двух состояний, «до» и «после», как это было в предыдущей главе. Эта схема была выражена Ньютоном в трёх законах, которые мы представим собственными словами Ньютона.
Закон 1: Каждое тело продолжает сохранять состояние покоя или равномерного прямолинейного движения, пока не будет вынуждено изменить это состояние под действием приложенной к нему силы.
Закон 2: Изменение движения (скорость изменения импульса) пропорционально приложенной движущей силе и происходит в направлении приложенной силы.
Закон 3: Каждому действию всегда соответствует равная реакция, или: взаимные действия двух тел всегда равны и направлены в противоположные стороны.
Смысл законов затуманен стилем изложения, выбранным Ньютоном для современников, для которых геометрия Эвклида представлялась самым прекрасным интеллектуальным памятником. В первом законе мы узнаём принцип инерции Галилея. Второй обычно выражается уравнением
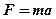 (3-1),
(3-1),
т.к. в большинстве случаев масса объекта не изменяется, и изменение импульса должно включать только изменение скорости. Скорость этого изменения является ускорением. А скорость изменения произведения массы на скорость равна произведению массы на ускорение.
Единица измерения силы определяется уравнением 3-1. Это сила, которая сообщает телу массой один килограмм ускорение в один метр на секунду в квадрате. Она называется Ньютоном (Н) и отражает практику, посредством которой физики сохраняют память и уважение к своим ушедшим коллегам в названии соответствующей единицы измерения. Третий закон легко понять, если мы заменим слово «действие» на «изменение импульса». То, что одно тело приобретает, другое тело должно потерять. Это просто закон сохранения импульса.
Решающий довод.
На первый взгляд, Ньютон очень мало добавил к работе Гюйгенса. Но это малое является решающим соображением, на котором держится полная теория движения.
Ньютон трактует передачу импульса от одного тела к другому как постепенный процесс и называет силой скорость, с которой эта передача происходит. Эффективность его подхода лежит в возможности обнаружить законы, которые предскажут, как будут действовать силы при взаимодействии двух тел.
Например, силу сопротивления воздуха, действующую на шар, можно получить по формуле, которая включает размер шара и скорость его движения; сила деформированной пружины зависит от того, как она сжата или растянута. Со времён Ньютона и до наших дней изучение движения сводится к поиску формул такого рода. Как только они найдены, каждую деталь движения можно предсказать, используя второй закон.
В «Принципах», однако, закон для одной силы был более важен, чем все другие. Это был закон тяготения Ньютона, который использовался им для объяснения движения Луны и планет в понятиях той же самой силы, которая управляет свободным падением тел на землю.
Это был его вызов картезианцам, который остался без ответа. Однако, до того как мы начнём изучать этот закон, необходимо представить себе, как в теории Ньютона рассматривается круговое движение.
Круговое движение.
Задача этого раздела – убедить вас, что круговое движение с постоянной скоростью на самом деле является ускоренным движением под действием силы, направленной к центру круга. Этот результат был ещё одним мало отмеченным вкладом Гюйгенса, однако Ньютон, видимо, получил его независимо некоторое время спустя.
Начнём аргументацию с обращения к вашей интуиции о том, что для изменения направления движения объекта необходима некая сила, направление которой не совпадает с направлением движения. Следующим шагом следует показать, что именно такая сила появляется, когда объект движется по кругу. Затем мы докажем сходство между круговым движением и более привычными формами ускоренного движения. Наконец, мы получим формулу для такого ускорения.
Представьте себе большой тяжёлый шар, который медленно катится по ровному полу. Если, находясь сзади него, мы толкаем его по направлению движения, то он ускорится. Аналогично, если мы находимся перед шаром и толкаем его в направлении, противоположном движению, шар замедлится.
Чтобы изменить направление движения шара, нужен толчок сбоку. Если этот толчок, в итоге, направлен по движению, шар ускорится и, вместе с тем, изменит направление движения. Если же толчок, в целом, произведён из положения перед шаром, он замедлится. Только толчок под прямым углом к направлению движения может изменить направление движения без изменения скорости.
Теперь привяжем к шару (всё ещё на полу) верёвку, другой конец которой закреплён на полу гвоздём. Шар будет двигаться по кругу. Конечно, в этом случае на шар действует вынуждающая сила: верёвка натянута, а гвоздь прочно вбит в пол. Шар может двигаться только в направлении, перпендикулярном верёвке, находясь на постоянном расстоянии от гвоздя. Верёвка может тянуть шар только в направлении к гвоздю. Если мы не будем учитывать трение и вызванное им замедление шара, то натяжение верёвки, будет оставаться постоянным. Итак, сила, действующая на шар, постоянна по величине, но непрерывно изменяет своё направление, всегда указывая на центр круга.
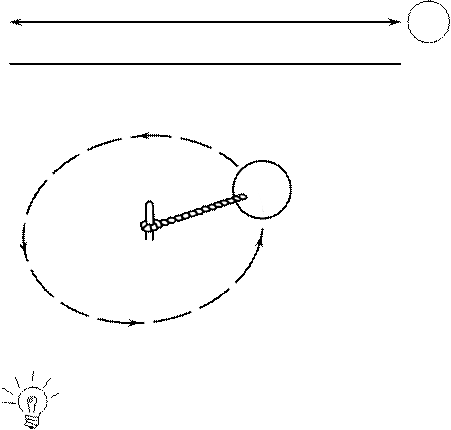
Предположим теперь, что мы поместили на полу на большом расстоянии от круга яркий источник света, и наблюдаем тень от шара на противоположной стене, как это показано на рис. 3-1. Тень движется «туда-сюда», как маятник, постоянно замедляясь, меняя направление движения на обратное, и снова ускоряясь.
Здесь мы применили принцип суперпозиции, чтобы рассмотреть движение шара только в одном направлении, игнорируя его движение в направлении к источнику света и движение от него. Мы получили очевидный пример ускоренного движения. Полное движение шара при этом можно представить суперпозицией двух движений под прямым углом друг к другу.
|


|

|

|
Каждый раз, когда шар проходит половину окружности, он изменяет движение на противоположное, совсем так, как если бы он остановился, а потом начал ускоряться в противоположном направлении. Если мы обозначим скорость шара υ, то она должна стать – υ, когда шар появится на противоположной стороне круга. Изменение скорости будет 2υ, совершенно также, как в случае шара, брошенного вертикально вверх, и возвращающегося на землю со скоростью противоположного направления. Чем быстрее движется шар, тем больше изменение скорости и, следовательно, больше ускорение. Чем быстрее движение, тем сильнее натянута верёвка.
Теперь, когда мы знаем изменение скорости шара, можно найти его среднее ускорение на пути в половину окружности. Чтобы сделать это, мы должны ещё знать, как долго продолжается весь процесс. А это зависит от того, насколько далеко шар уходит от центра своего движения и насколько быстро он движется. Длина окружности радиуса r равна 2πr, и шар проходит половину этого пути. Время необходимое для этого, равно расстоянию, делённому на скорость, 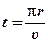 . По определению ускорения мы получаем
. По определению ускорения мы получаем
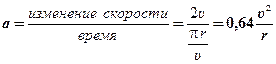 . . |
Однако мы должны помнить, что это среднее ускорение и общий результат действия силы, которая за время прохождения пол-оборота тянула шар в разных направлениях. В самом деле, в конце пути сила имеет направление прямо противоположное тому, которое было в начале. Поэтому мгновенное ускорение должно быть, конечно же, больше. Однако строгий расчёт мгновенного ускорения требует некоторых математических понятий, которые мы избегаем в этой книге. Поэтому просто представим результат как
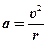 . (3-2) . (3-2) |
С точки зрения здравого смысла, значение этой формулы понять не трудно. Наличие r в знаменателе просто означает, что требуется большая сила, чтобы удержать объект на малом круге, чем на большом, потому что он вращается на малом быстрее ( 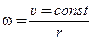 ). Тридцать миль в час – комфортная скорость при смене полосы на шоссе. Но если вы огибаете угол здания в городе на этой скорости, вы услышите громкий визг покрышек. Они визжат потому, что не любят иметь дело с силой, перпендикулярной их движению. В числителе находится υ, и в квадрате, потому что пропорциональность ускорения и скорости нелинейно ухудшает ситуацию: 1) приходится изменять так же бóльшую скорость, 2) это изменение должно происходить более быстро. Радиус безопасного поворота на скорости 60 миль/час не в 2, но в 4 раза больше, чем на скорости 30 миль/час.
). Тридцать миль в час – комфортная скорость при смене полосы на шоссе. Но если вы огибаете угол здания в городе на этой скорости, вы услышите громкий визг покрышек. Они визжат потому, что не любят иметь дело с силой, перпендикулярной их движению. В числителе находится υ, и в квадрате, потому что пропорциональность ускорения и скорости нелинейно ухудшает ситуацию: 1) приходится изменять так же бóльшую скорость, 2) это изменение должно происходить более быстро. Радиус безопасного поворота на скорости 60 миль/час не в 2, но в 4 раза больше, чем на скорости 30 миль/час.
В качестве последнего примера применения этой формулы, рассмотрим путь гоночной машины, проходящей поворот, как показано на рис. 3-2.  Хороший гонщик входит в поворот по внешней полосе, движется к внутренней полосе в середине поворота и заканчивает поворот на его внешней границе. Такой путь имеет максимально возможный радиус кривизны, и это позволяет машине поддерживать максимальную скорость.
Хороший гонщик входит в поворот по внешней полосе, движется к внутренней полосе в середине поворота и заканчивает поворот на его внешней границе. Такой путь имеет максимально возможный радиус кривизны, и это позволяет машине поддерживать максимальную скорость.
Если вам не нравится думать о круговом движении с постоянной скоростью как об ускоренном, то это может быть связано с тем неудобством, которое создаёт использование слов то из физики, то из обычной речи, где слово ускорение однозначно предполагает, что что-то начинает двигаться быстрее. В физике же это слово означает любое отклонение от инерциального движения. Мы уже видели, как простое изменение знака решает проблему замедления. В этой части книги мы просто двинулись ещё на один шаг дальше от использования слова ускорение в обычном разговорном языке.
