Теорема о разбиении множества отношением эквивалентности на классы
Определение 27. Бинарное отношение R на множестве А называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно.
Пример. «∥» на множестве всех прямых в пространстве, «=» на множестве ℝ.
Определение 28. Пусть А - непустое множество. Совокупность А1,...,Аn непустых подмножеств множества А называется разбиением множества А на классы (при этом сами множества А1,...,Аn называют классами), если каждый элемент множества А принадлежит одному и только одному из подмножеств А1,...,Аn, т.е.
1) А1 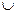 ...
... 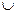 Аn=A;
Аn=A;
2) Ai 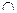 A j =
A j = 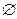 , i=
, i= 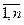 , j=
, j= 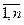 , j≠i.
, j≠i.
Пример 1. Пусть А={1,2,3}. Тогда
1) A1={1}, A2={2}, A3={3} – разбиение А;
2) B1={123} – разбиение А.
Теорема 2. Пусть R - отношение эквивалентности на множестве А.Тогда множество А разбивается отношением R на классы, которые называются классами эквивалентности, а множество этих классов обозначается A/R (A по R) и называется фактормножеством множества А по отношению эквивалентности R.
Доказательство. Пусть R отношение эквивалентности на А.
Пусть а  А, aR={x
А, aR={x  A| (a,x)
A| (a,x)  R}(*)
R}(*)
Отметим, что aR 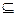 A,
A, 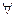 а
а  А.
А.
Покажем что подмножества вида (*) образуют разбиение множества А. Для этого достаточно показать, что они удовлетворяют усл.1 и усл.2 из определения 28.
Усл.1) Покажем что 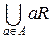 =А
=А
а) Покажем что 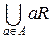
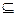 А
А
Действительно, т.к. 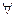 а
а  А: аR
А: аR 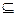 А
А 
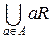
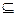 А
А
б) Покажем что А 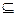
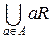
Пусть b  A. Покажем, что b
A. Покажем, что b 
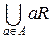 . Действительно, т.к. R- отношение эквивалентности
. Действительно, т.к. R- отношение эквивалентности  R-рефлексивно
R-рефлексивно  (b,b)
(b,b)  R
R  x=b
x=b  bR
bR 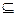
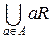
 А
А 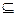
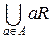
Из а) и б) 
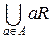 =А
=А
Усл. 2) Пусть aR 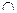 bR
bR 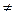
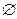 . Покажем, что вв этом случае aR=bR.
. Покажем, что вв этом случае aR=bR.
а) Покажем, что aR 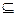 bR . Для этого ∀xÎaR покажем, что xÎbR.
bR . Для этого ∀xÎaR покажем, что xÎbR.
Т.к. aR 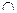 bR
bR 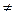
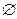

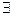 с
с  аR
аR 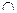 bR. Тогда выполняются условия(1) c
bR. Тогда выполняются условия(1) c  aR
aR
и (2) c  bR
bR
Согласно (*), из x  aR
aR  (a,x)
(a,x)  R
R
Аналогично, из (1)  (a,c)
(a,c)  R, и поскольку R симметрично, то (c,a)
R, и поскольку R симметрично, то (c,a)  R. Ввиду транзит ивности R, из (c,a)
R. Ввиду транзит ивности R, из (c,a)  R и (a,x)
R и (a,x)  R
R  (c,x)
(c,x)  R
R
Далее, из (2)  (b,c)
(b,c)  R. Ввиду транзитивности R, из (b,c)
R. Ввиду транзитивности R, из (b,c)  R и (c,x)
R и (c,x)  R
R  (b,x)
(b,x)  R
R  x
x  bR
bR
Значит, aR 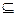 bR.
bR.
б) Покажем bR 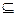 aR
aR
T.к. aR 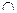 bR=
bR= 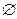

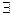 c
c  bR
bR 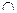 aR
aR
(1)c  bR и (2) с
bR и (2) с  аR
аR
Пусть x  bR
bR  (b,x)
(b,x)  R
R
Из (1)  (b,c)
(b,c)  R
R  (c,x)
(c,x)  R
R  (b,x)
(b,x)  R
R
Из (2)  (a,c)
(a,c)  R
R  (a,x)
(a,x)  R
R  x
x  aR
aR
Значит, bR 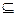 aR
aR
Из а) и б) заключаем, что aR=bR.
Вывод: из Усл.1) и Усл.2) следует, что множество А разбивается отношением R на классы вида (*).
