Теорема о биссектрисе внутреннего угла треугольника

ТЕОРЕМА синусов: Во всяком треугольнике стороны пропорциональны синусам противолежащих углов. Отношение стороны к синусу противолежащего угла равно диаметру описанной около треугольника окружности, то есть: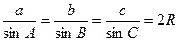

ТЕОРЕМА косинусов: Во всяком треугольнике квадрат стороны, лежащей против некоторого угла, равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними, то есть: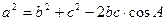

Следствие.

В треугольнике квадрат большей стороны равен сумме квадратов двух других сторон тогда и только тогда, когда треугольник прямоугольный. В треугольнике квадрат большей стороны меньше суммы квадратов двух других сторон тогда и только тогда, когда треугольник остроугольный.

В треугольнике квадрат большей стороны больше суммы квадратов двух других сторон тогда и только тогда, когда треугольник тупоугольный.

ТЕОРЕМА Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

Задания с решениями

1.Найдите большую диагональ ромба, сторона которого равна 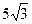, а острый угол равен 60º.

Решение

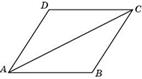
Так как угол А равен 60º, то угол D равен 120º. Применим теорему косинусов к треугольнику ADC.

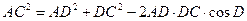, то есть .

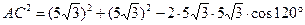Так как 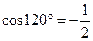, то получаем

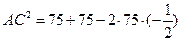
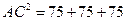
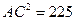
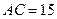
Ответ 15

2.Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 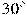. Найдите радиус окружности, описанной около этого треугольника.

Решение

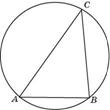
По теореме синусов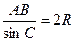

Тогда 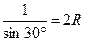. Откуда получаем 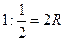, 2R= 2, R=1

Ответ 1

3.Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Решение

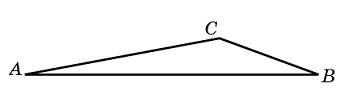
По теореме синусов 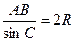, но .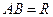

Тогда получаем 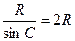. Откуда следует, что .

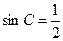Так как угол С тупой, то угол С равен 150º

Ответ 150º

4. Площадь треугольника АВС равна 50, АС = 10, угол С равен 30 º.Найти АВ

Решение

Площадь треугольника АВС можно найти по формуле 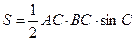.С учетом того, что АС = 10, угол С равен 30º,а S=50, получим уравнение .

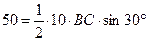Тогда , , .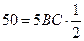

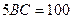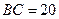Найдем АВ по теореме косинусов.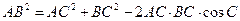

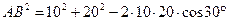
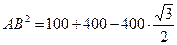
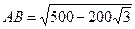
Ответ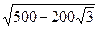

5. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.

Решение

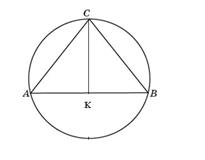
Проведем высоту СК. Так как треугольник равнобедренный, то СК медиана и АК=КВ=24

Из треугольника АСК найдем по теореме Пифагора СК.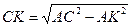

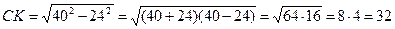
Из треугольника АСК найдем синус угла А.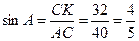

По теореме синусов для треугольника АВС имеем .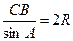

Тогда 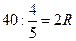, 2R=50, R=25.

Ответ 25.

6. В равнобедренном треугольнике косинус угла при вершине равен 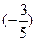, Основание треугольника равно 6 .Найти длину боковой стороны

Решение

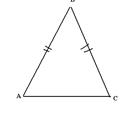
Обозначим 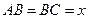Применим теорему косинусов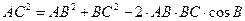

Подставим значения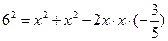

Получаем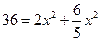

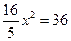
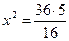
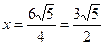
Ответ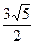

7. Стороны треугольника равны 25 , 39 и 56 .Найти площадь треугольника и косинус большего из углов.

Решение

Пусть АС=39,ВС=25,АВ=56.Тогда больший из углов –это угол С

Определим вид угла С. 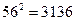, 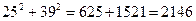.Так как 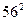> 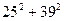, то угол С тупой.

Найдем площадь по формуле Герона.

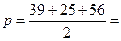
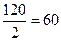
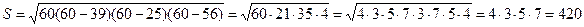
С другой стороны,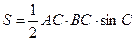

Получаем 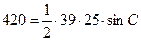, откуда 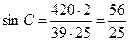Тогда так как угол С тупой, то

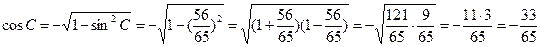
Вторым способом можно найти косинус угла С по теореме косинусов: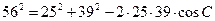

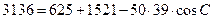
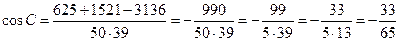
Ответ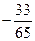

8. Катеты прямоугольного треугольника равны 6 и 8 .найти отрезки, на которые делит гипотенузу биссектриса прямого угла треугольника.

Решение

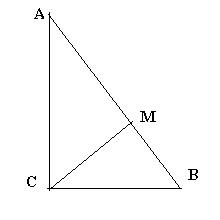
Пусть АС=8, ВС=6

По теореме Пифагора найдем АВ.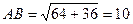

Пусть СМ – биссектриса. Обозначим АМ=х, тогда МВ=10-х

По свойству биссектрисы внутреннего угла треугольника имеем 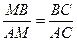, то есть получаем уравнение 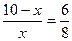. Откуда ,

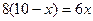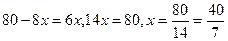
То есть АМ= 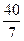, тогда МВ=10- =

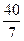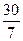
Ответ 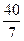,